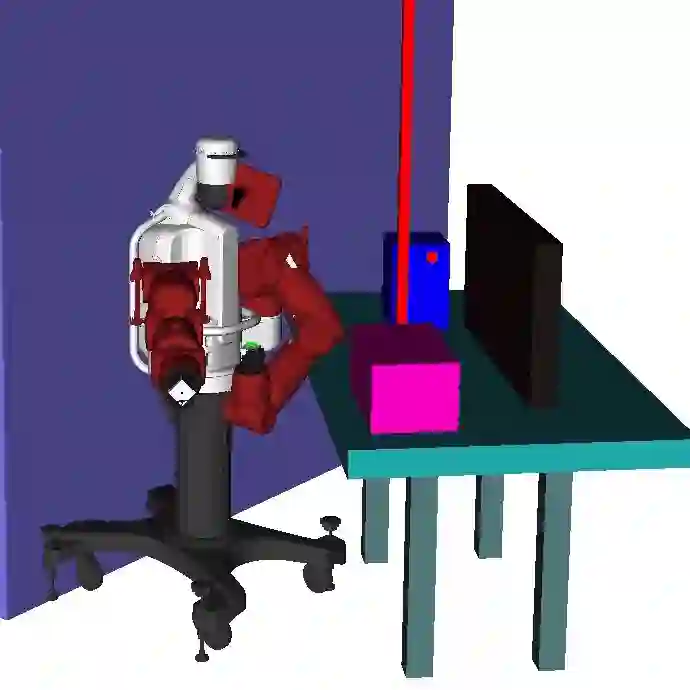
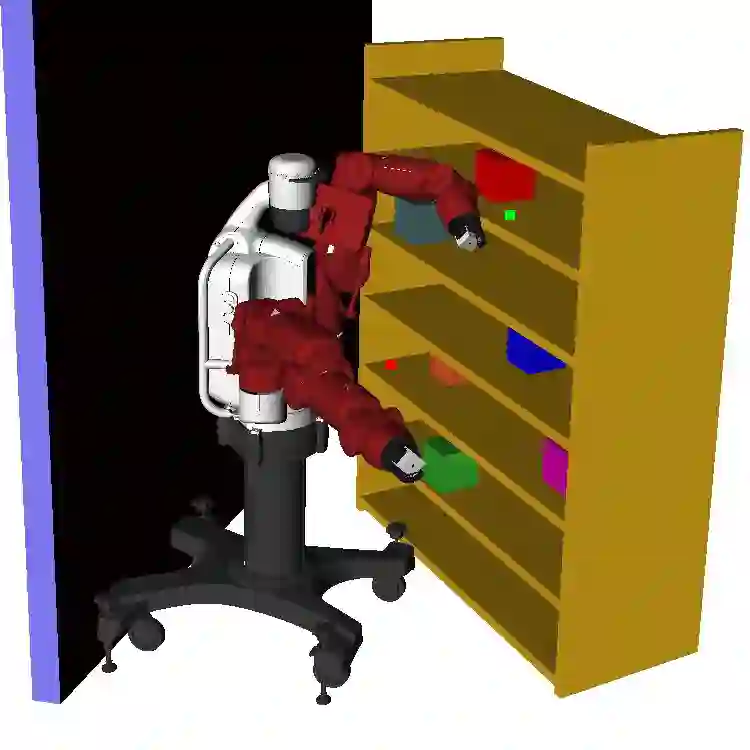
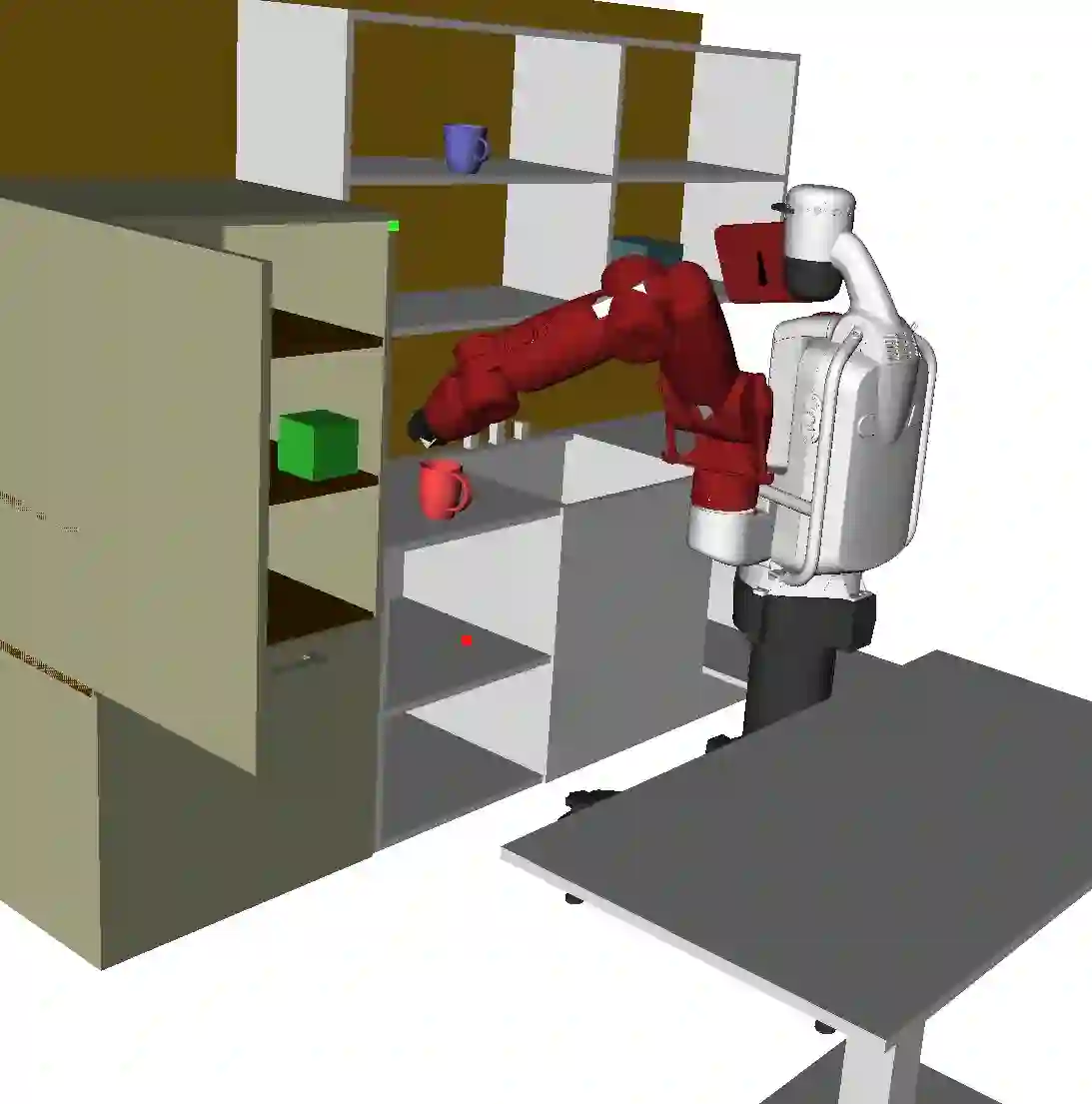
Many real-world robotic operations that involve high-dimensional humanoid robots require fast-reaction to plan disturbances and probabilistic guarantees over collision risks, whereas most probabilistic motion planning approaches developed for car-like robots can not be directly applied to high-dimensional robots. In this paper, we present probabilistic Chekov (p-Chekov), a fast-reactive motion planning system that can provide safety guarantees for high-dimensional robots suffering from process noises and observation noises. Leveraging recent advances in machine learning as well as our previous work in deterministic motion planning that integrated trajectory optimization into a sparse roadmap framework, p-Chekov demonstrates its superiority in terms of collision avoidance ability and planning speed in high-dimensional robotic motion planning tasks in complex environments without the convexification of obstacles. Comprehensive theoretical and empirical analysis provided in this paper shows that p-Chekov can effectively satisfy user-specified chance constraints over collision risk in practical robotic manipulation tasks.
翻译:许多涉及高维人形机器人的现实世界机器人操作需要快速反应,以规划碰撞风险的扰动和概率保障,而为汽车类机器人开发的大多数概率运动规划方法不能直接适用于高维机器人。本文介绍了一种快速反应运动规划系统Chekov(p-Chekov)的概率性(p-Chekov),这是一个快速反应运动规划系统,可为受过程噪音和观测噪音影响的高维机器人提供安全保障。 利用机器学习的最新进展以及我们先前在确定性运动规划方面的工作,将轨迹优化纳入稀有的路线图框架,p-Chekov展示了其在复杂环境中避免碰撞的能力和规划速度方面的优势,而没有将障碍混为一谈。本文提供的综合理论和经验分析表明,p-Chekov可以有效地满足用户在实际机器人操纵任务中针对碰撞风险确定的机会限制。