On Numerical Solution of Structural model for the Probability of Default under a Regime-Switching Synchronous-Jump Tempered Stable Lévy Model with Desingularized Meshfree Collocation method

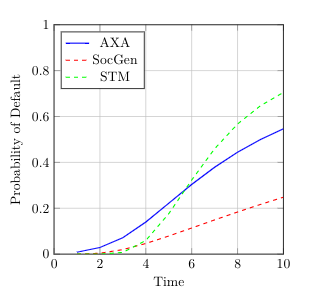
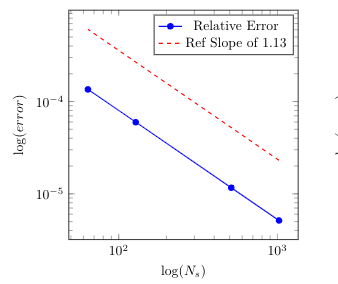
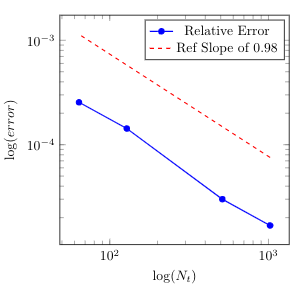
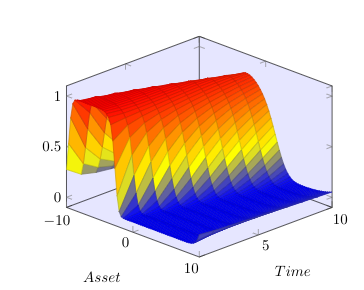
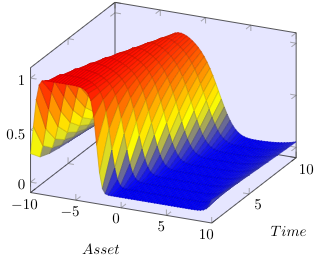
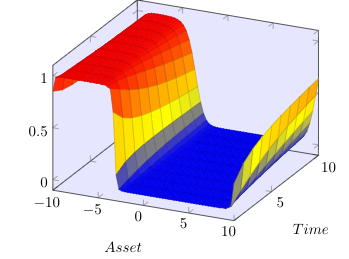
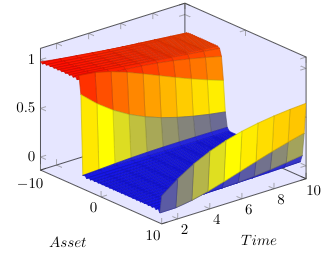
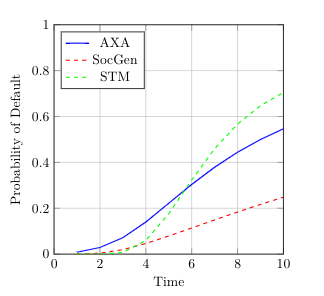
In the paper [Hainaut, D. and Colwell, D.B., A structural model for credit risk with switching processes and synchronous jumps, The European Journal of Finance44(33) (4238):3262-3284], the authors exploit a synchronous-jump regime-switching model to compute the default probability of a publicly-traded company. Here, we first generalize the proposed L\'evy model to a more general setting of tempered stable processes recently introduced into the finance literature. Based on the singularity of the resulting partial integro-differential operator, we propose a general framework based on strictly positive-definite functions to de-singularize the operator. We then analyze an efficient meshfree collocation method based on radial basis functions to approximate the solution of the corresponding system of partial integro-differential equations arising from the structural credit risk model. We show that under some regularity assumptions, our proposed method naturally de-sinularizes the problem in the tempered stable case. Numerical results of applying the method on some standard examples from the literature confirm the accuracy of our theoretical results and numerical algorithm.