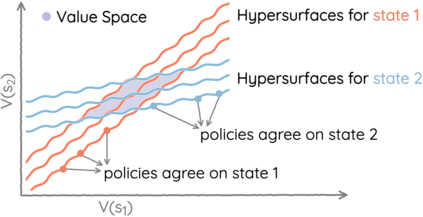
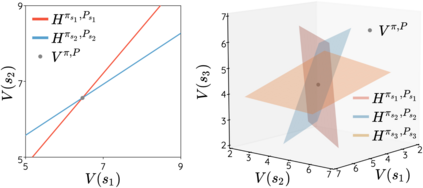
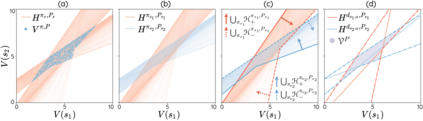
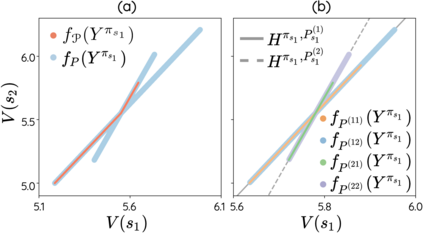
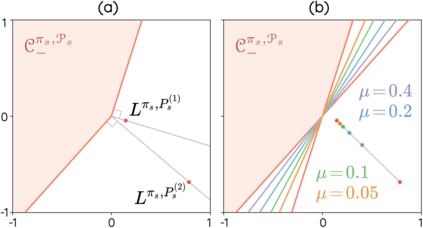
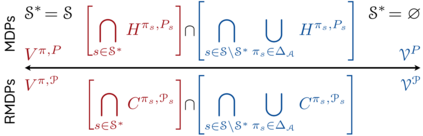
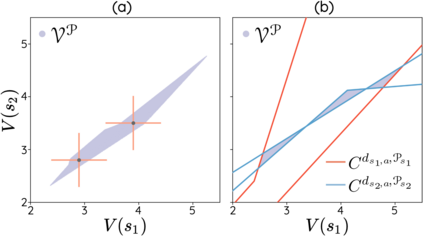
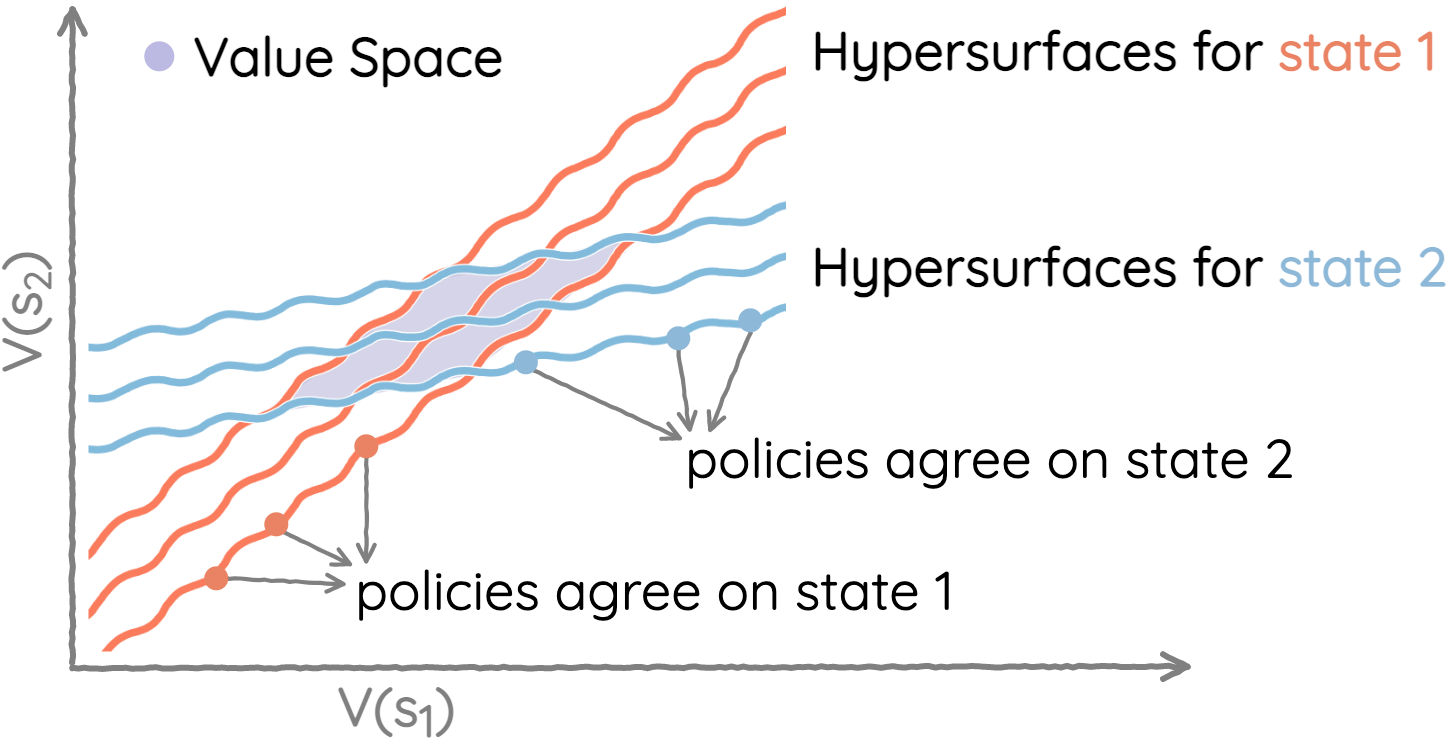
The space of value functions is a fundamental concept in reinforcement learning. Characterizing its geometric properties may provide insights for optimization and representation. Existing works mainly focus on the value space for Markov Decision Processes (MDPs). In this paper, we study the geometry of the robust value space for the more general Robust MDPs (RMDPs) setting, where transition uncertainties are considered. Specifically, since we find it hard to directly adapt prior approaches to RMDPs, we start with revisiting the non-robust case, and introduce a new perspective that enables us to characterize both the non-robust and robust value space in a similar fashion. The key of this perspective is to decompose the value space, in a state-wise manner, into unions of hypersurfaces. Through our analysis, we show that the robust value space is determined by a set of conic hypersurfaces, each of which contains the robust values of all policies that agree on one state. Furthermore, we find that taking only extreme points in the uncertainty set is sufficient to determine the robust value space. Finally, we discuss some other aspects about the robust value space, including its non-convexity and policy agreement on multiple states.
翻译:价值函数空间是强化学习的基本概念。 定位其几何特性可以提供优化和代表的洞察力。 现有工作主要侧重于Markov 决策进程(MDPs)的值空间。 在本文中, 我们研究了更一般的强力 MDPs(RMDPs)设置的强力价值空间的几何, 考虑的是过渡不确定性。 具体地说, 由于我们发现很难直接适应之前对RMDPs采取的方法, 我们从重新审视非强力事件开始, 并引入新的视角, 使我们能够以类似的方式描述非强力和强力的价值空间。 这个视角的关键是以州的方式将价值空间分解为超表层的结合。 我们通过分析, 显示强力价值空间是由一组锥形超表层决定的, 每个表层都包含所有就一个州达成一致的政策的强力价值。 此外, 我们发现, 仅仅从不确定性组中的极端点就足以确定稳健的价值空间。 最后, 我们讨论关于强力价值空间的其他方面, 包括它无法连接的多面政策协议。