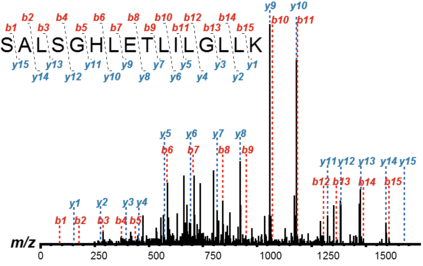
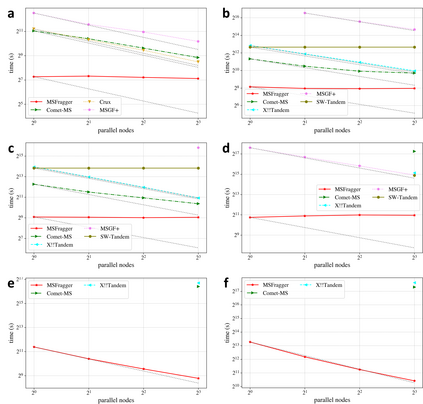
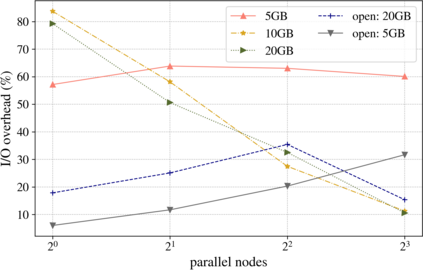
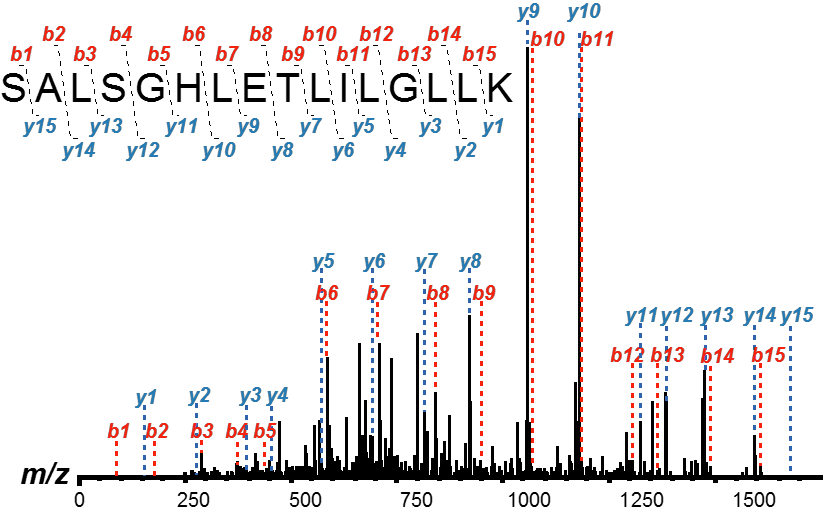
Mass spectrometry (MS) based omics data analysis require significant time and resources. To date, few parallel algorithms have been proposed for deducing peptides from mass spectrometry-based data. However, these parallel algorithms were designed, and developed when the amount of data that needed to be processed was smaller in scale. In this paper, we prove that the communication bound that is reached by the \emph{existing} parallel algorithms is $\Omega(mn+2r\frac{q}{p})$, where $m$ and $n$ are the dimensions of the theoretical database matrix, $q$ and $r$ are dimensions of spectra, and $p$ is the number of processors. We further prove that communication-optimal strategy with fast-memory $\sqrt{M} = mn + \frac{2qr}{p}$ can achieve $\Omega({\frac{2mnq}{p}})$ but is not achieved by any existing parallel proteomics algorithms till date. To validate our claim, we performed a meta-analysis of published parallel algorithms, and their performance results. We show that sub-optimal speedups with increasing number of processors is a direct consequence of not achieving the communication lower-bounds. We further validate our claim by performing experiments which demonstrate the communication bounds that are proved in this paper. Consequently, we assert that next-generation of \emph{provable}, and demonstrated superior parallel algorithms are urgently needed for MS based large systems-biology studies especially for meta-proteomics, proteogenomic, microbiome, and proteomics for non-model organisms. Our hope is that this paper will excite the parallel computing community to further investigate parallel algorithms for highly influential MS based omics problems.
翻译:以质量光谱学为基础的基于 质量光谱学的数据分析需要大量的时间和资源。 到目前为止, 几乎没有提议使用平行算法来从基于质量光谱的数据中除去peptides。 然而, 这些平行算法是设计出来的, 当需要处理的数据数量在规模上缩小时, 这些平行算法是开发的。 在本文中, 我们证明由\emph{ 存在} 平行算法( memega) (mn+2r\frac{q ⁇ p}) 所连接的通信可以达到$( mmn+2r\frac{q ⁇ p} $ 。 美元和美元是理论数据库矩阵的维度, 美元和美元是平行的, 美元是光谱学的维度, 美元是用来证实我们快速模型的运行结果, 并且我们通过运行一个快速的直线算算法, 也证明了我们运行一个直线的运行结果, 运行一个直径直径直的运算法, 以我们运行一个直径直径直的运行的算算算法, 运行一个直直的算算算, 以我们运行一个直算算算法的运行的运行的运行的运行的运行的运行结果, 。