Optimal local approximation spaces for parabolic problems

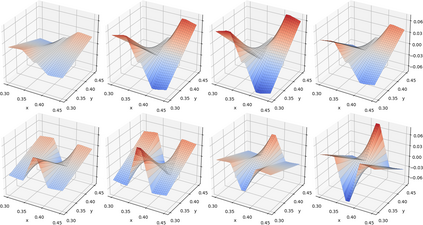
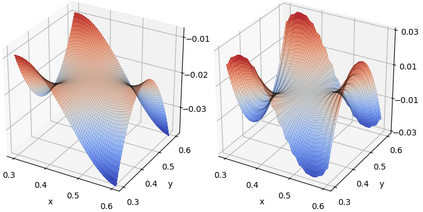
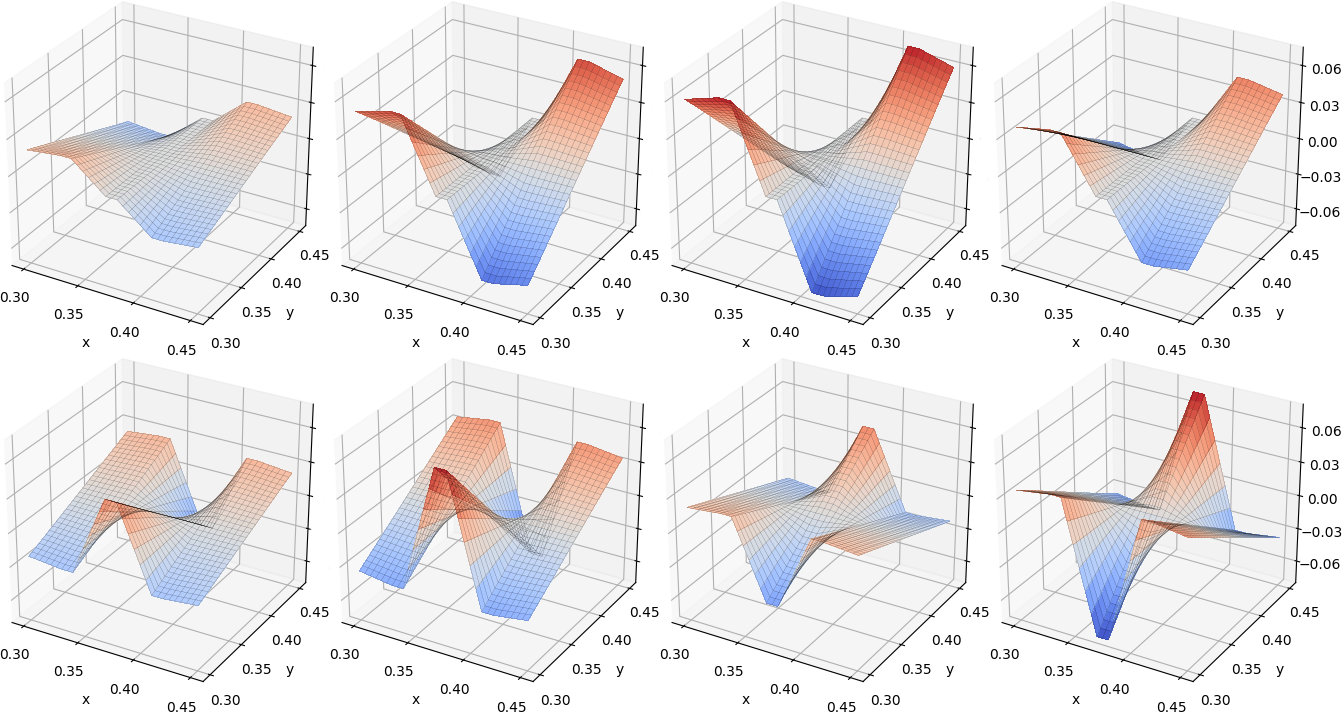
We propose local space-time approximation spaces for parabolic problems that are optimal in the sense of Kolmogorov and may be employed in multiscale and domain decomposition methods. The diffusion coefficient can be arbitrarily rough in space and time. To construct local approximation spaces we consider a compact transfer operator that acts on the space of local solutions and covers the full time dimension. The optimal local spaces are then given by the left singular vectors of the transfer operator. To proof compactness of the latter we combine a suitable parabolic Caccioppoli inequality with the compactness theorem of Aubin-Lions. In contrast to the elliptic setting [I. Babu\v{s}ka and R. Lipton, Multiscale Model. Simul., 9 (2011), pp. 373-406] we need an additional regularity result to combine the two results. Furthermore, we employ the generalized finite element method to couple local spaces and construct an approximation of the global solution. Since our approach yields reduced space-time bases, the computation of the global approximation does not require a time stepping method and is thus computationally efficient. Moreover, we derive rigorous local and global a priori error bounds. In detail, we bound the global approximation error in a graph norm by the local errors in the $L^2(H^1)$-norm, noting that the space the transfer operator maps to is equipped with this norm. Numerical experiments demonstrate an exponential decay of the singular values of the transfer operator and the local and global approximation errors for problems with high contrast or multiscale structure regarding space and time.