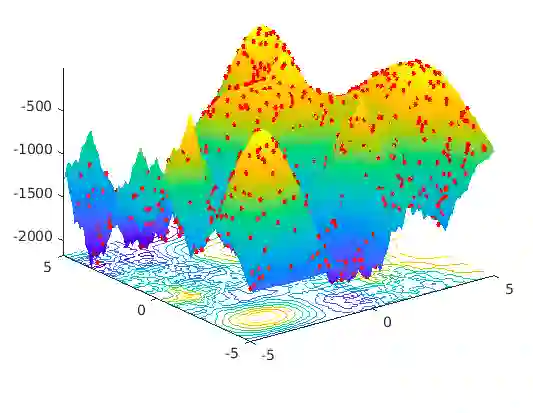
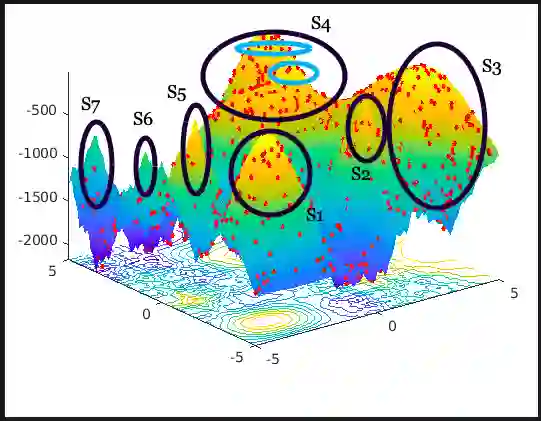
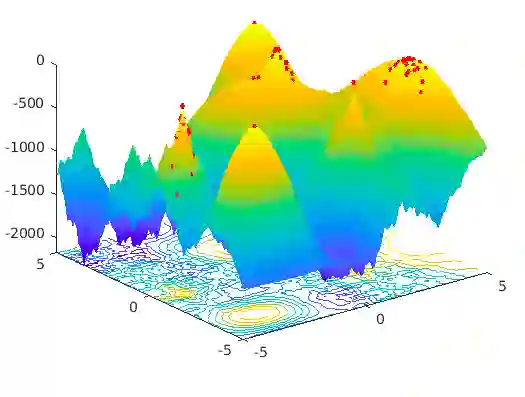
Most of the real-world problems are multimodal in nature that consists of multiple optimum values. Multimodal optimization is defined as the process of finding multiple global and local optima (as opposed to a single solution) of a function. It enables a user to switch between different solutions as per the need while still maintaining the optimal system performance. Classical gradient-based methods fail for optimization problems in which the objective functions are either discontinuous or non-differentiable. Evolutionary Algorithms (EAs) are able to find multiple solutions within a population in a single algorithmic run as compared to classical optimization techniques that need multiple restarts and multiple runs to find different solutions. Hence, several EAs have been proposed to solve such kinds of problems. However, Differential Evolution (DE) algorithm is a population-based heuristic method that can solve such optimization problems, and it is simple to implement. The potential challenge in Multi-Modal Optimization Problems (MMOPs) is to search the function space efficiently to locate most of the peaks accurately. The optimization problem could be to minimize or maximize a given objective function and we aim to solve the maximization problems on multimodal functions in this study. Hence, we have proposed an algorithm known as Enhanced Opposition Differential Evolution (EODE) algorithm to solve the MMOPs. The proposed algorithm has been tested on IEEE Congress on Evolutionary Computation (CEC) 2013 benchmark functions, and it achieves competitive results compared to the existing state-of-the-art approaches.
翻译:现实世界的大多数问题都是由多种最佳价值构成的多式联运问题。多模式优化被定义为找到多种全球和本地的功能选择(而不是单一的解决方案)的过程。它使用户能够根据需要而转换不同的解决方案,同时保持最佳系统性能。经典的梯度法在优化问题上失败,其中目标功能要么不连续,要么没有差异。进化性演算法(EAs)能够在人群中找到多种解决方案,与需要多重重新启动和多重运行以找到不同解决方案的典型优化技术相比,在一个单一的算法运行中找到多种解决方案。因此,一些EA被提议解决这类问题。然而,差异性演进(DE)算法是一种基于人口、可以解决这种优化问题且易于执行的超理论方法。多模式优化性优化调算法问题(MMOP)的潜在挑战是寻找功能空间,以便准确定位大多数现有峰值。优化问题可能是最大限度地减少或最大限度地优化一个特定的目标功能,我们的目标是解决这类类型的问题。我们提出的升级的进化(IMOFAL-R)的进化算法功能是用来解决进化的进化和进化的进化的进化方法。我们所了解的进化的进化的进化方法的进化的进化的进化方法。在研究中,对改进的进化的进化法的进化法的进化法的进化法的进化(进化方法进行了进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化学的进化学的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的进化法的