Mean-field Behaviour of Neural Tangent Kernel for Deep Neural Networks

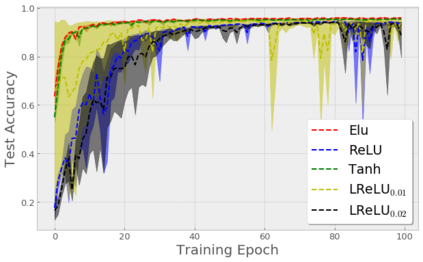
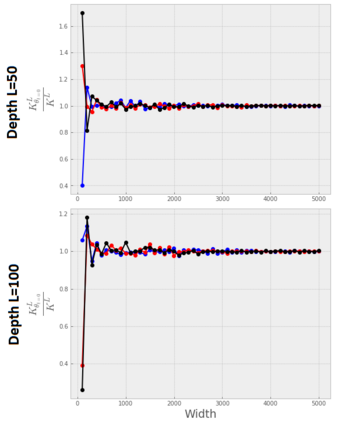
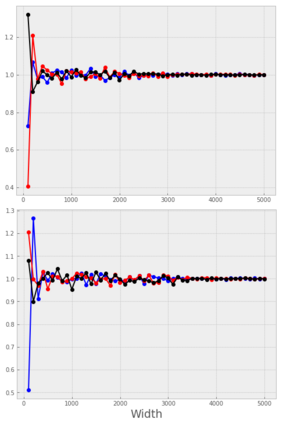
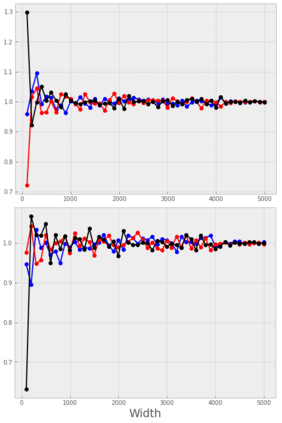
Recent work by Jacot et al. (2018) has showed that training a neural network of any kind with gradient descent in parameter space is equivalent to kernel gradient descent in function space with respect to the Neural Tangent Kernel (NTK). Lee et al. (2019) built on this result to show that the output of a neural network trained using full batch gradient descent can be approximated by a linear model for wide networks. In parallel, a recent line of studies (Schoenholz et al. (2017), Hayou et al. (2019)) suggested that a special initialization known as the Edge of Chaos leads to good performance. In this paper, we bridge the gap between these two concepts and show the impact of the initialization and the activation function on the NTK as the network depth becomes large. We provide experiments illustrating our theoretical results.