Bayesian sequential data assimilation for COVID-19 forecasting

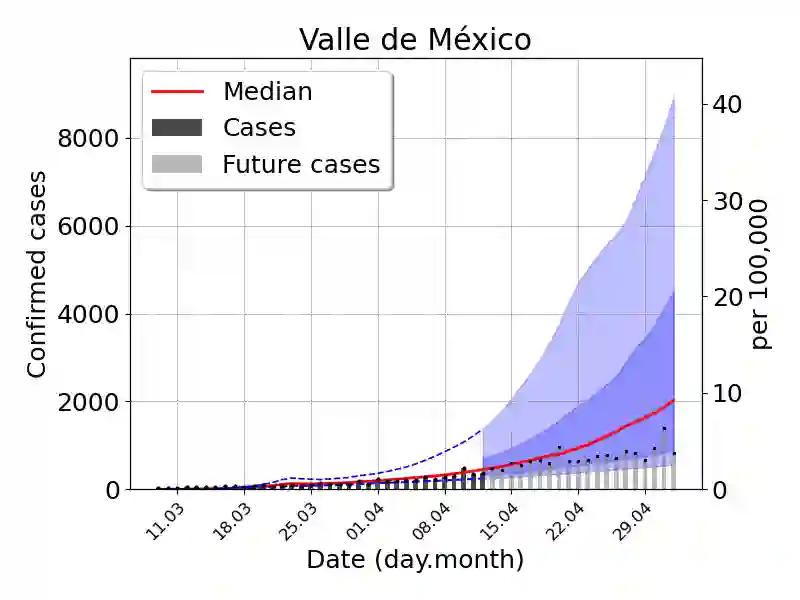
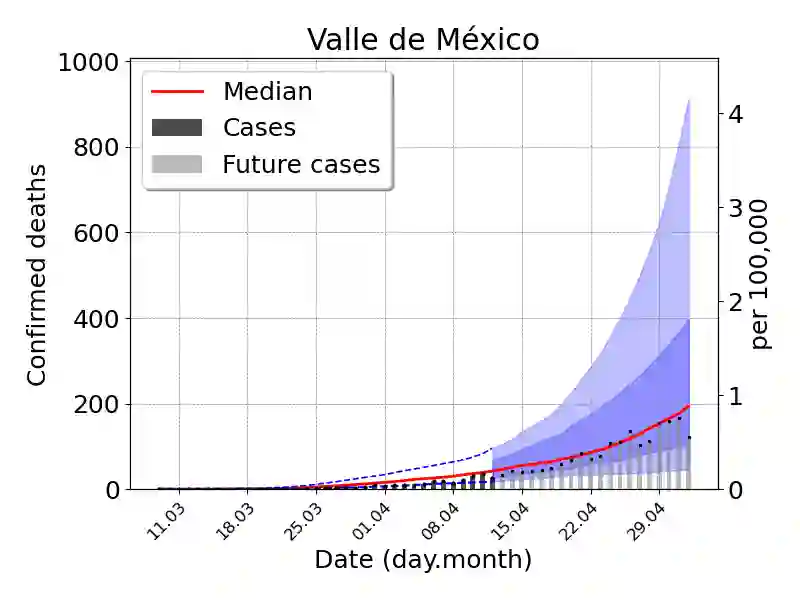
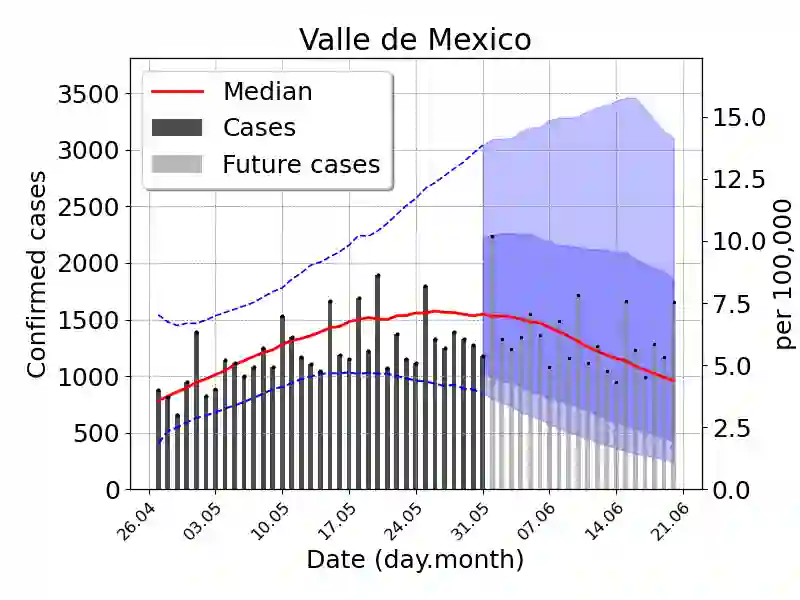
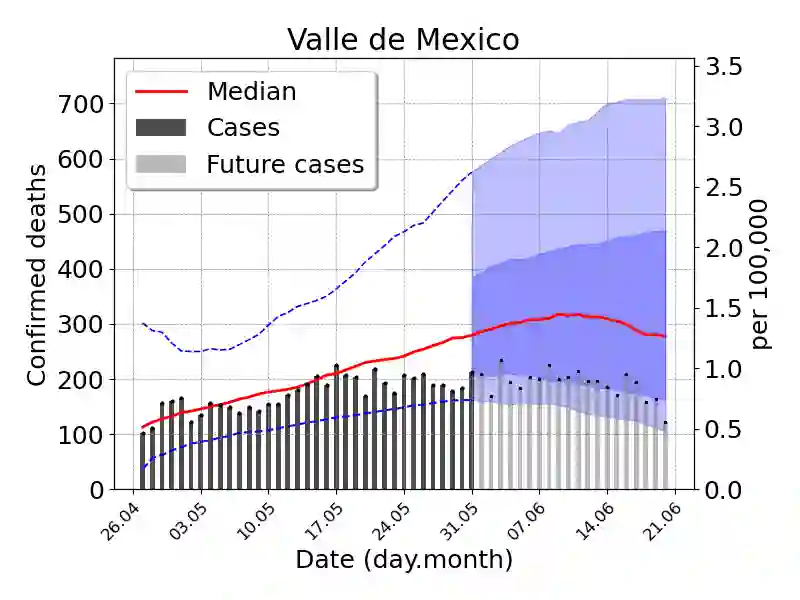
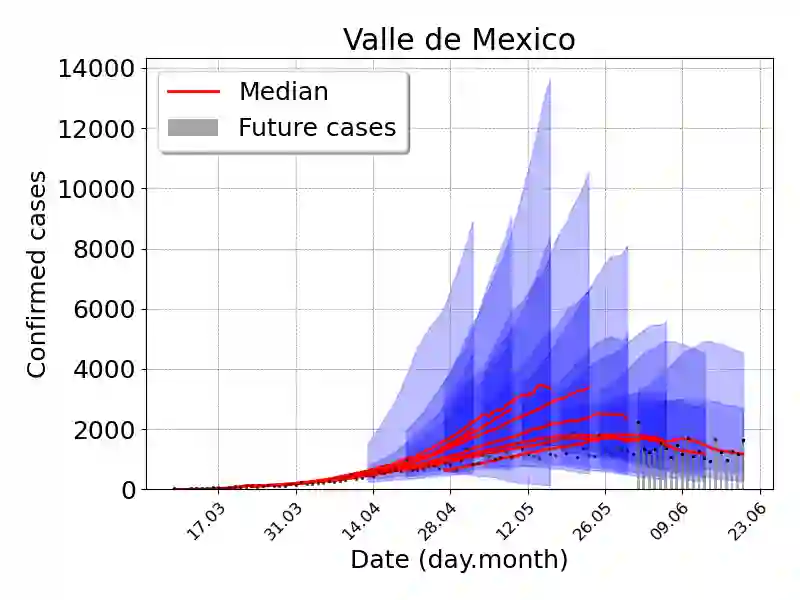
We introduce a Bayesian sequential data assimilation method for COVID-19 forecasting. It is assumed that suitable transmission, epidemic and observation models are available and previously validated and the transmission and epidemic models are coded into a dynamical system. The observation model depends on the dynamical system state variables and parameters, and is cast as a likelihood function. We elicit prior distributions of the effective population size, the dynamical system initial conditions and infectious contact rate, and use Markov Chain Monte Carlo sampling to make inference and prediction of quantities of interest (QoI) at the onset of the epidemic outbreak. The forecast is sequentially updated over a sliding window of epidemic records as new data becomes available. Prior distributions for the state variables at the new forecasting time are assembled using the dynamical system, calibrated for the previous forecast. Moreover, changes in the contact rate and effective population size are naturally introduced through auto-regressive models on the corresponding parameters. We show our forecasting method's performance using a SEIR type model and COVID-19 data from several Mexican localities.