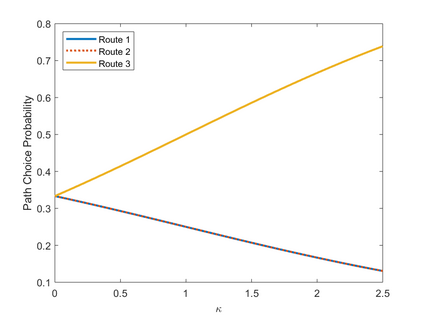
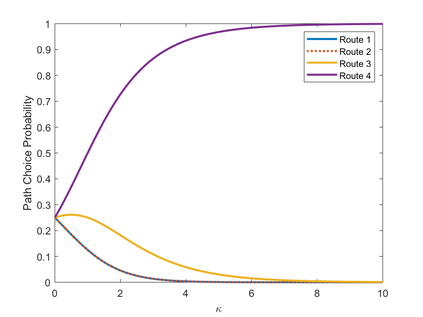
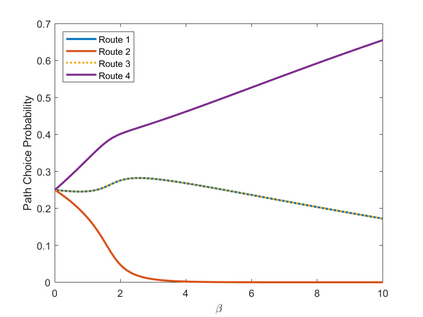
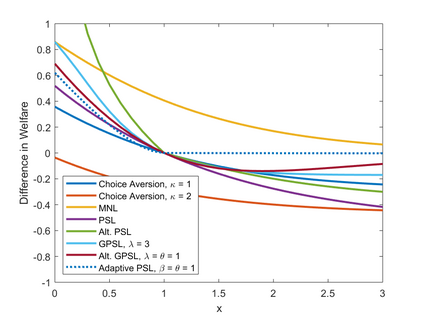
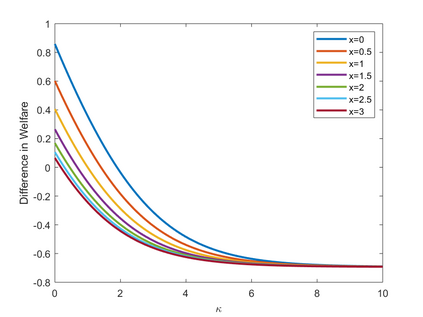
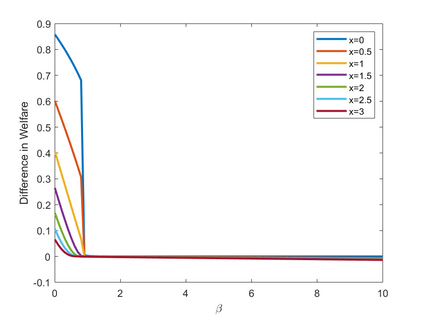
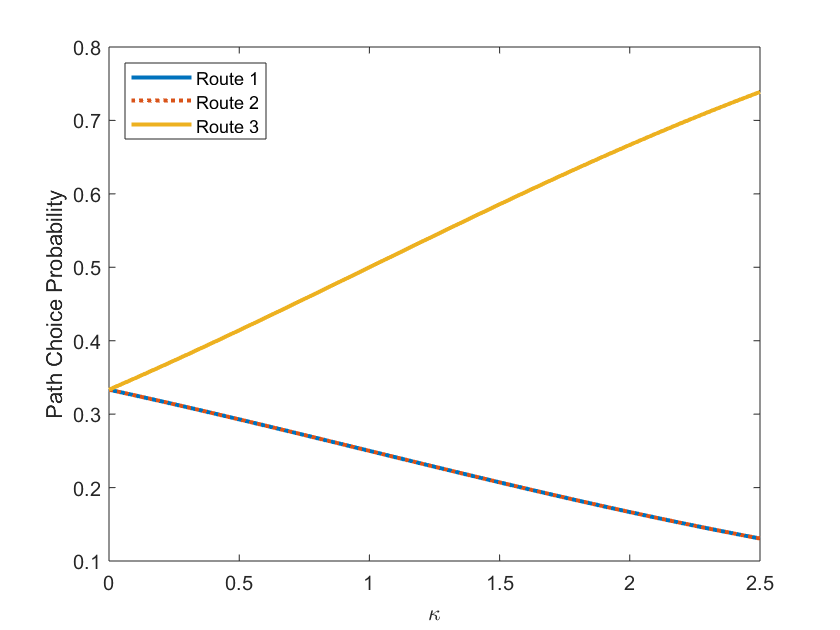
We propose a recursive logit model which captures the notion of choice aversion by imposing a penalty term that accounts for the dimension of the choice set at each node of the transportation network. We make three contributions. First, we show that our model overcomes the correlation problem between routes, a common pitfall of traditional logit models, and that the choice aversion model can be seen as an alternative to these models. Second, we show how our model can generate violations of regularity in the path choice probabilities. In particular, we show that removing edges in the network may decrease the probability for existing paths. Finally, we show that under the presence of choice aversion, adding edges to the network can make users worse off. In other words, a type of Braess's paradox can emerge outside of congestion and can be characterized in terms of a parameter that measures users' degree of choice aversion. We validate these contributions by estimating this parameter over GPS traffic data captured on a real-world transportation network.
翻译:我们提出一个循环逻辑模型,通过对运输网络的每个节点所设定的选择范围实施一个惩罚性术语来说明选择反向的概念。 我们做出了三点贡献。 首先,我们表明我们的模型克服了路线之间的关联问题,传统逻辑模型的共同陷阱,选择反向模型可以被视为这些模型的替代物。 其次,我们展示了我们的模型如何在路径选择概率方面产生违反规则的情况。特别是,我们显示,网络的去除边缘可能会降低现有路径的概率。最后,我们表明,在选择反常的情况下,增加网络的边缘可以使用户更加糟糕。换句话说,一种布拉斯的悖论可以在交通堵塞之外出现,并且可以用一个参数来测量用户选择反向的程度。我们通过估计这个参数来验证这些贡献,而不是在现实世界运输网络上捕获的GPS交通数据。