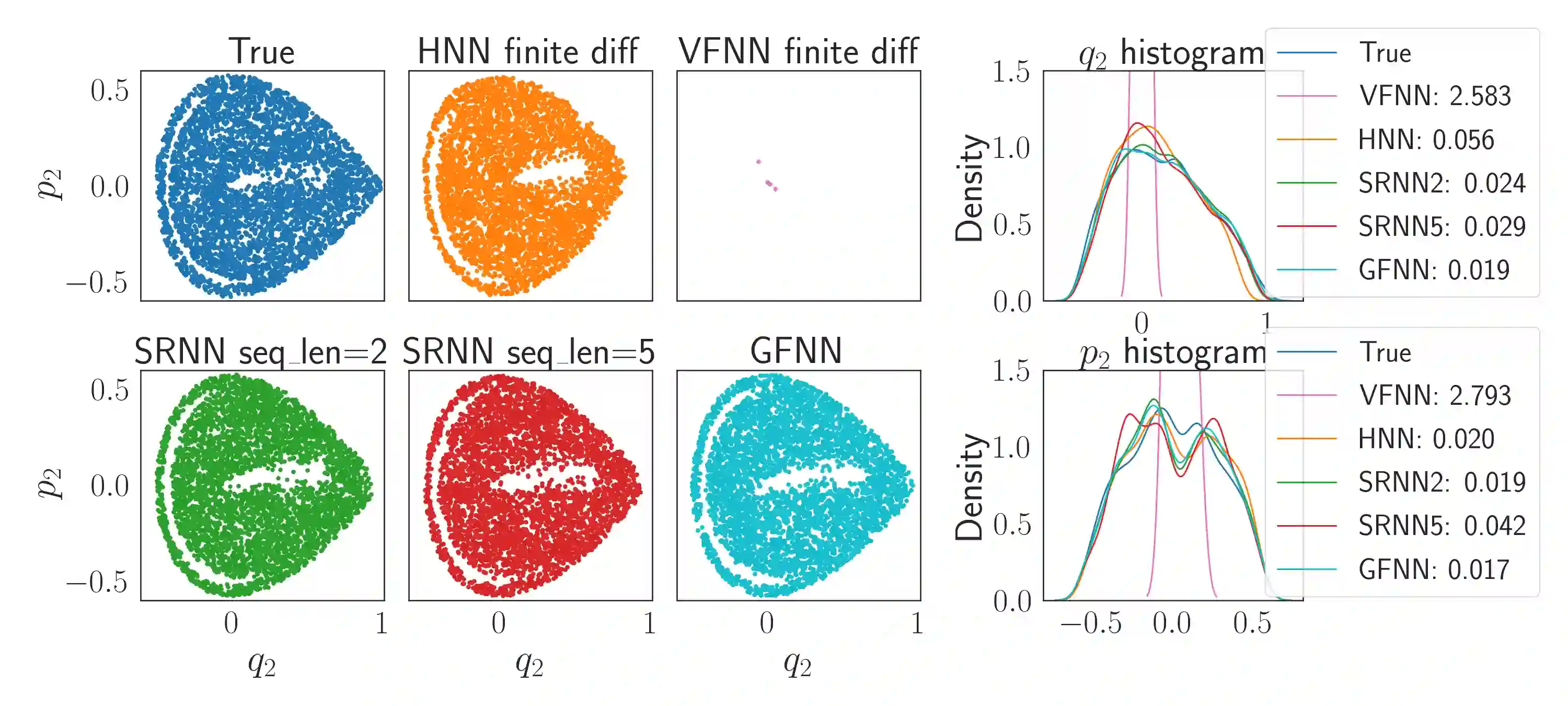
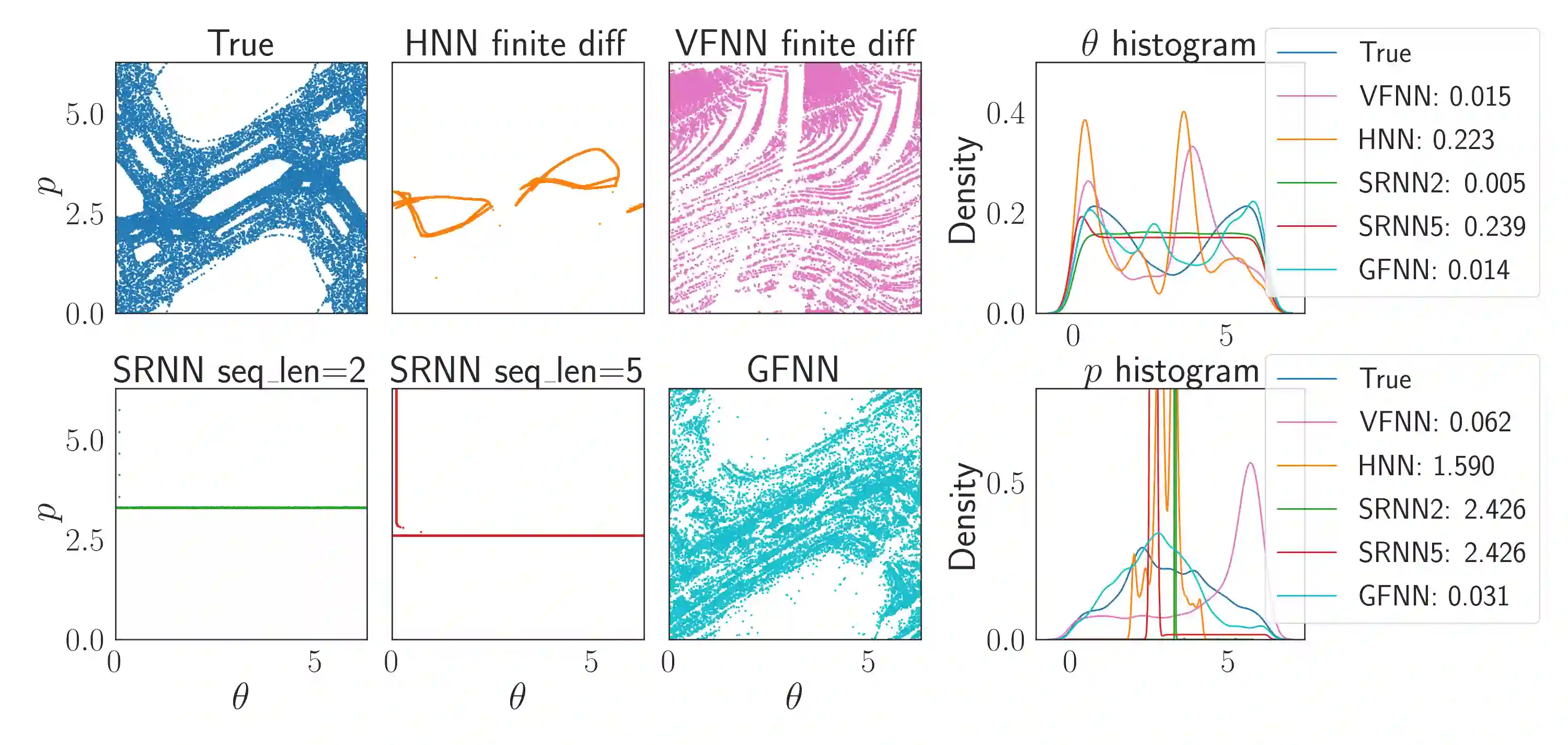
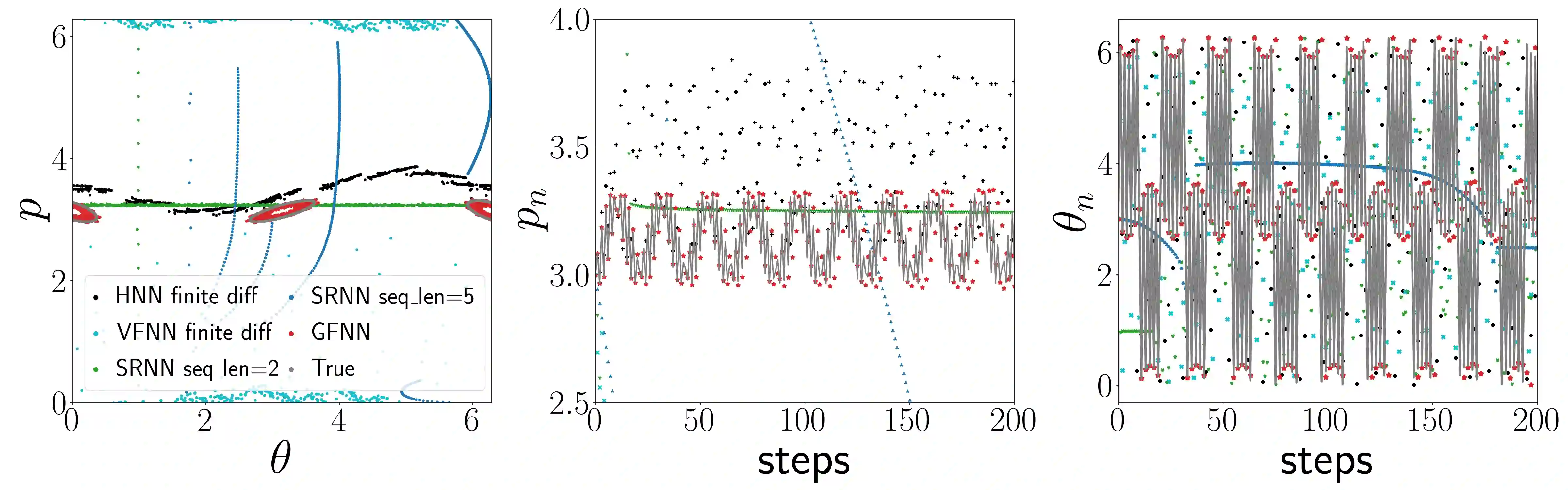
We consider the learning and prediction of nonlinear time series generated by a latent symplectic map. A special case is (not necessarily separable) Hamiltonian systems, whose solution flows give such symplectic maps. For this special case, both generic approaches based on learning the vector field of the latent ODE and specialized approaches based on learning the Hamiltonian that generates the vector field exist. Our method, however, is different as it does not rely on the vector field nor assume its existence; instead, it directly learns the symplectic evolution map in discrete time. Moreover, we do so by representing the symplectic map via a generating function, which we approximate by a neural network (hence the name GFNN). This way, our approximation of the evolution map is always \emph{exactly} symplectic. This additional geometric structure allows the local prediction error at each step to accumulate in a controlled fashion, and we will prove, under reasonable assumptions, that the global prediction error grows at most \emph{linearly} with long prediction time, which significantly improves an otherwise exponential growth. In addition, as a map-based and thus purely data-driven method, GFNN avoids two additional sources of inaccuracies common in vector-field based approaches, namely the error in approximating the vector field by finite difference of the data, and the error in numerical integration of the vector field for making predictions. Numerical experiments further demonstrate our claims.
翻译:我们考虑的是由潜伏的分布式地图产生的非线性时间序列的学习和预测。 一个特例是汉密尔顿系统(不一定分解), 其解决方案流提供了这样的分布式地图。 对于这个特例, 两种基于学习潜伏的 ODE 矢量场的通用方法, 以及基于学习生成矢量场的汉密尔顿人所存在的专门方法。 然而, 我们的方法是不同的, 因为它不依赖矢量场, 也不假定它的存在; 相反, 它直接在离散时间里学习了共性进化进化图。 此外, 我们通过生成功能代表共性地图图, 我们通过一个神经网络( 名称为 GFNN) 的近似。 对于这个特例, 我们进化图的近似总是 emph{ exactly} 符号性方法。 这种额外的地理测量结构使得每一步的本地预测错误可以以控制的方式累积, 并且根据合理的假设, 全球预测误差在大多数 emph{线性 } 来这样做。 我们通过一个长的预测性地图时间来代表共振测测测测图性地图的地图场,, 从而在以不变的 的数值系中, 的数值系中, 的数值系中, 进一步地数据源值的数值系中, 进一步地显示着一个基于的数值系的数值系的数值系的实地的数据源值的数值系中的数据源的 。