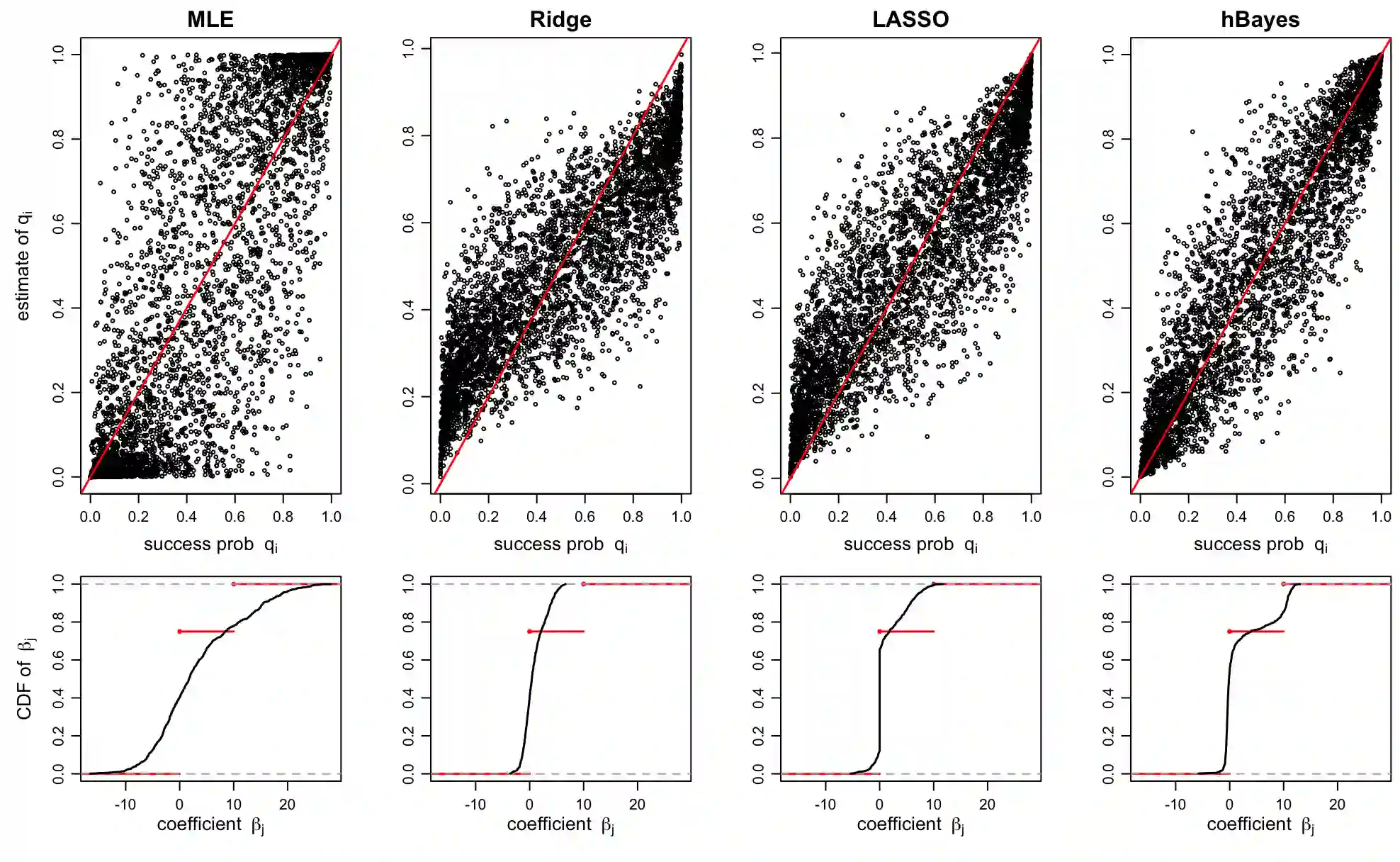
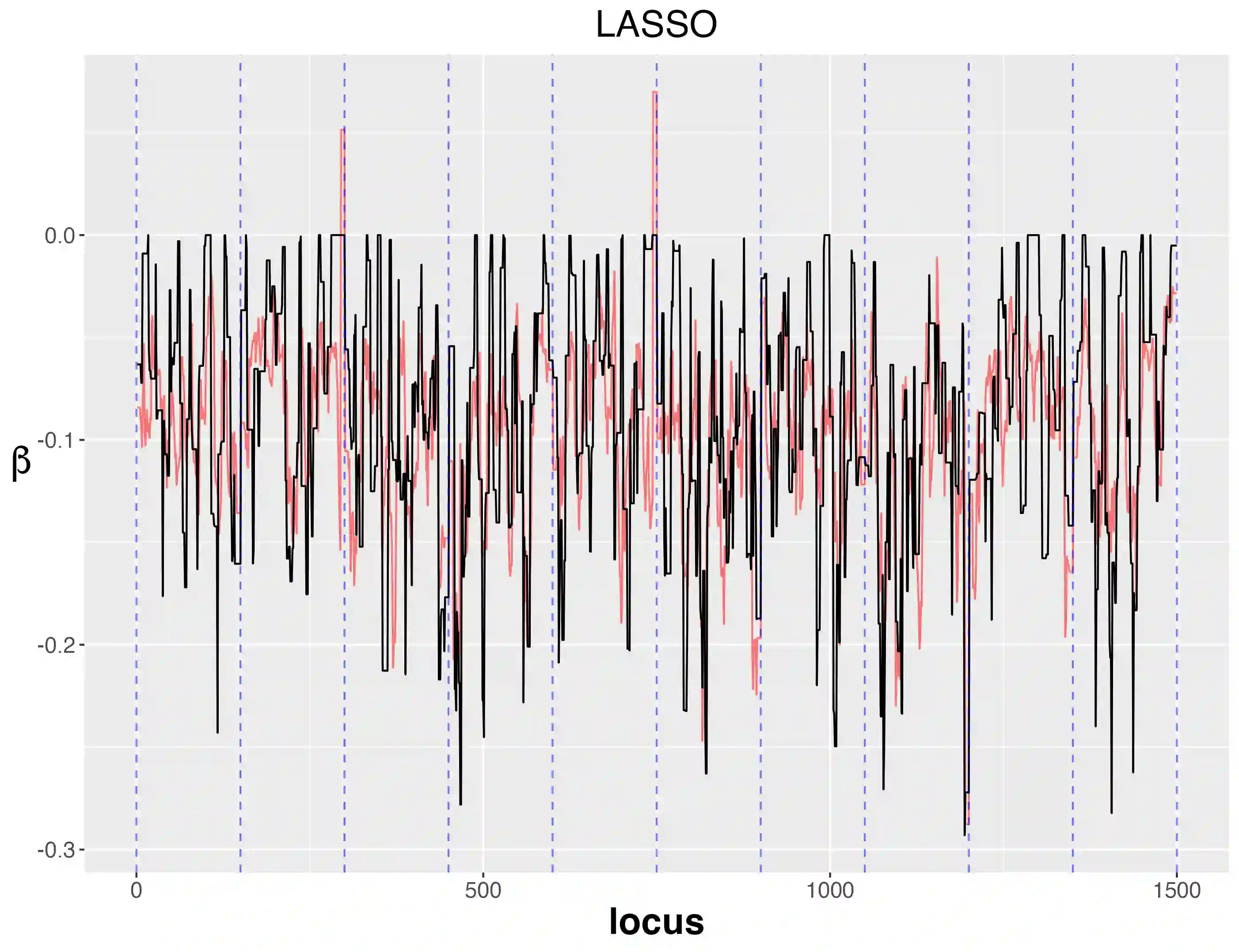
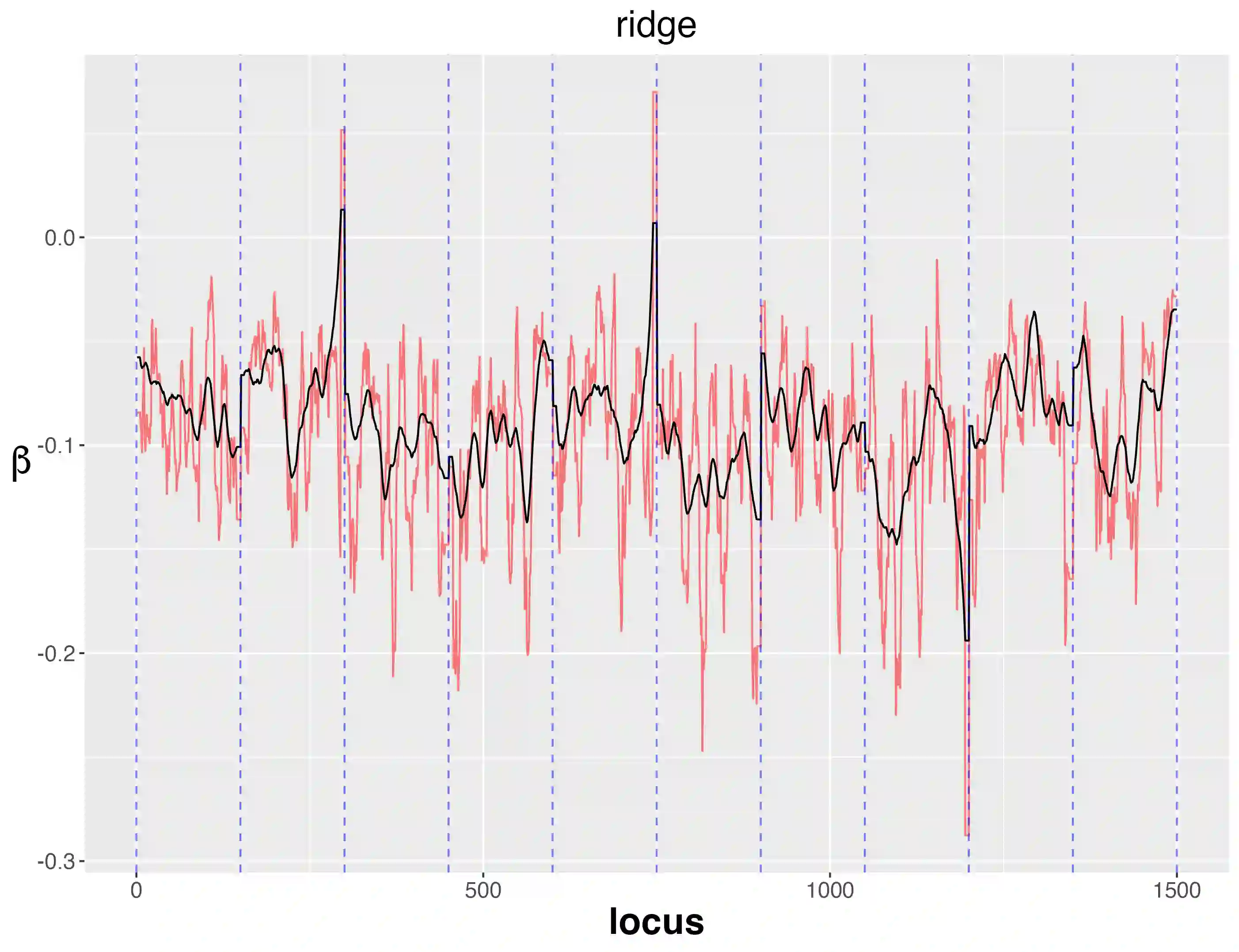
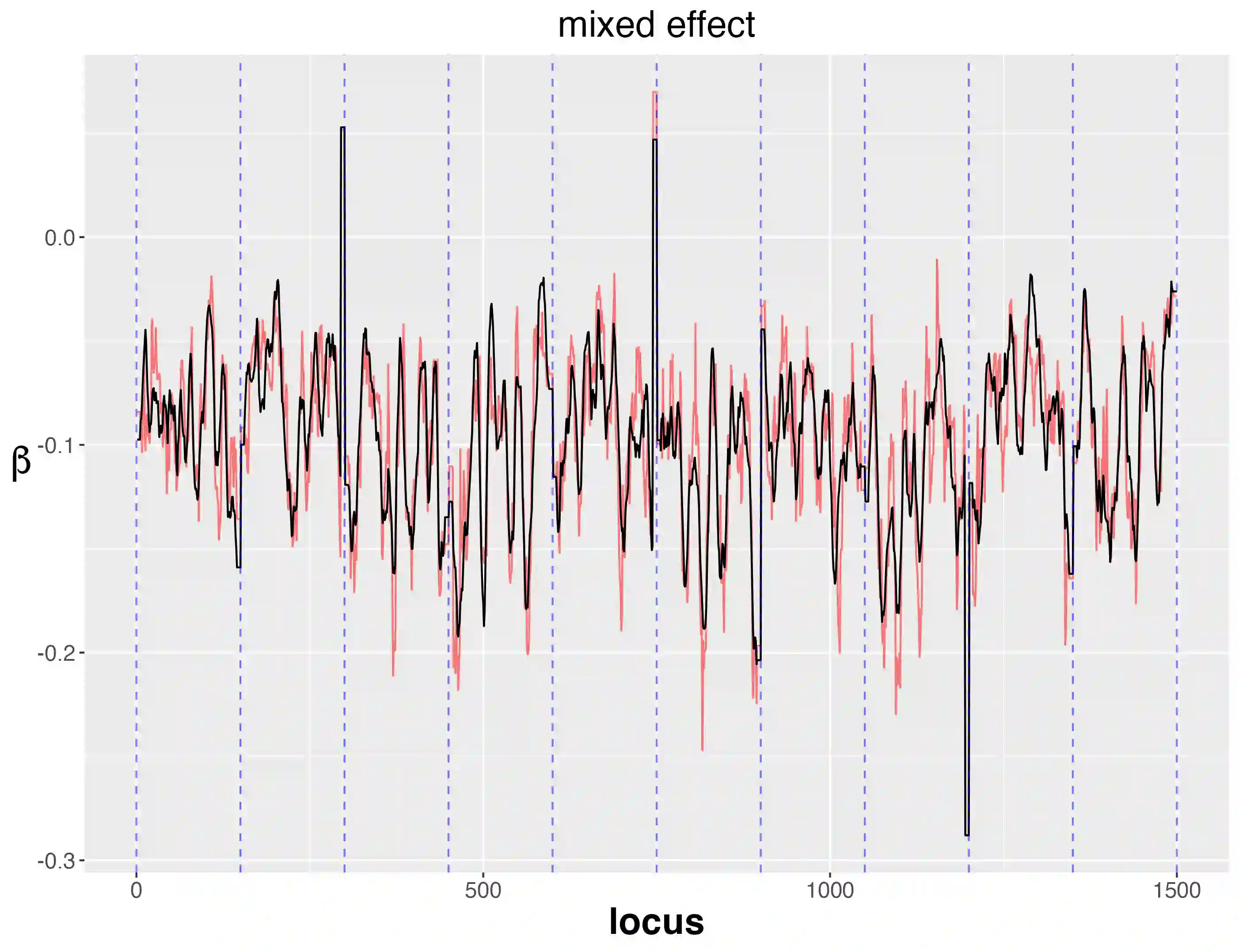
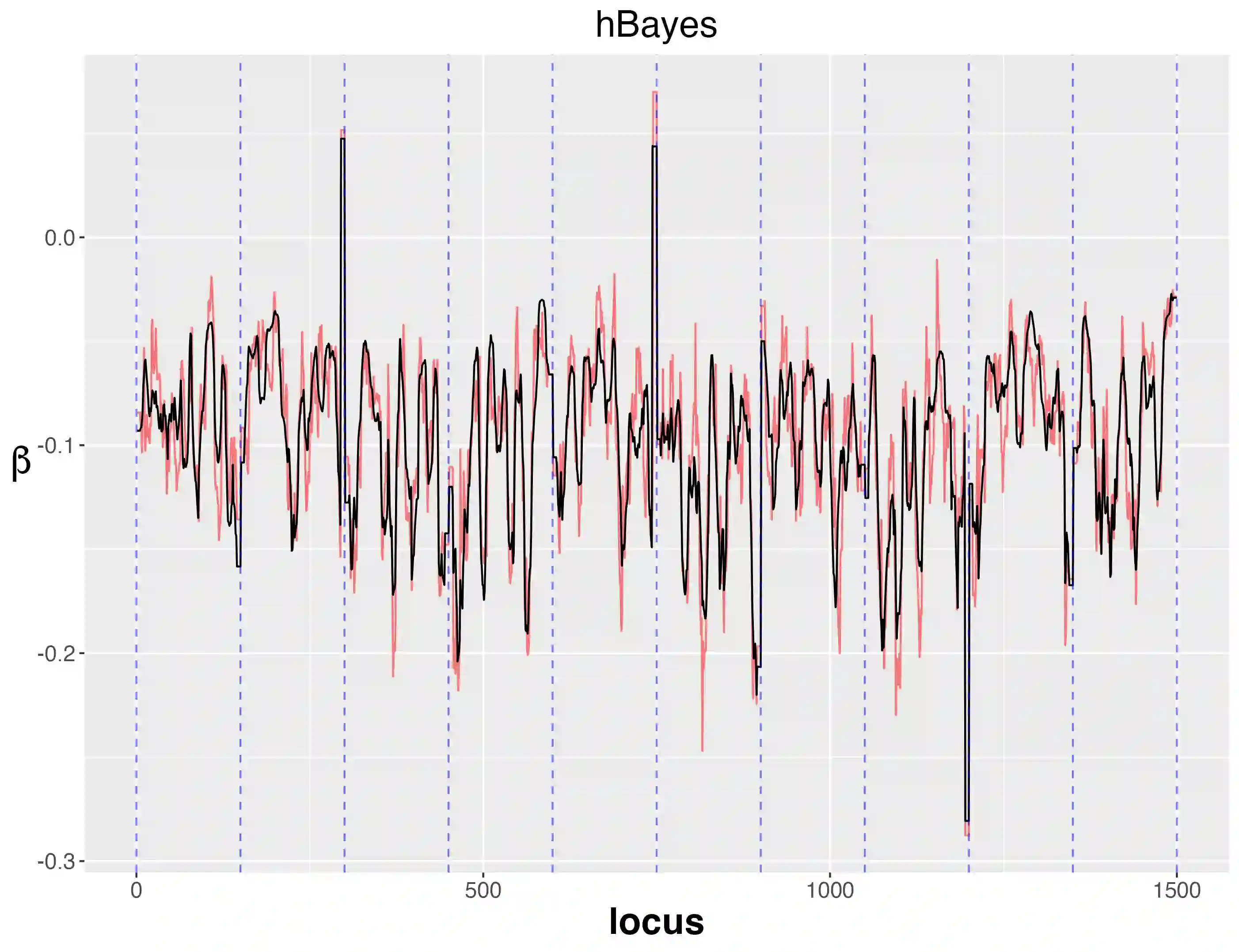
In a given generalized linear model with fixed effects, and under a specified loss function, what is the optimal estimator of the coefficients? We propose as a contender an ideal (oracle) shrinkage estimator, specifically, the Bayes estimator under the particular prior that assigns equal mass to every permutation of the true coefficient vector. We first study this ideal shrinker, showing some optimality properties in both frequentist and Bayesian frameworks by extending notions from Robbins's compound decision theory. To compete with the ideal estimator, taking advantage of the fact that it depends on the true coefficients only through their {\it empirical distribution}, we postulate a hierarchical Bayes model, that can be viewed as a nonparametric counterpart of the usual Gaussian hierarchical model. More concretely, the individual coefficients are modeled as i.i.d.~draws from a common distribution $\pi$, which is itself modeled as random and assigned a Polya tree prior to reflect indefiniteness. We show in simulations that the posterior mean of $\pi$ approximates well the empirical distribution of the true, {\it fixed} coefficients, effectively solving a nonparametric deconvolution problem. This allows the posterior estimates of the coefficient vector to learn the correct shrinkage pattern without parametric restrictions. We compare our method with popular parametric alternatives on the challenging task of gene mapping in the presence of polygenic effects. In this scenario, the regressors exhibit strong spatial correlation, and the signal consists of a dense polygenic component along with several prominent spikes. Our analysis demonstrates that, unlike standard high-dimensional methods such as ridge regression or Lasso, the proposed approach recovers the intricate signal structure, and results in better estimation and prediction accuracy in supporting simulations.
翻译:暂无翻译