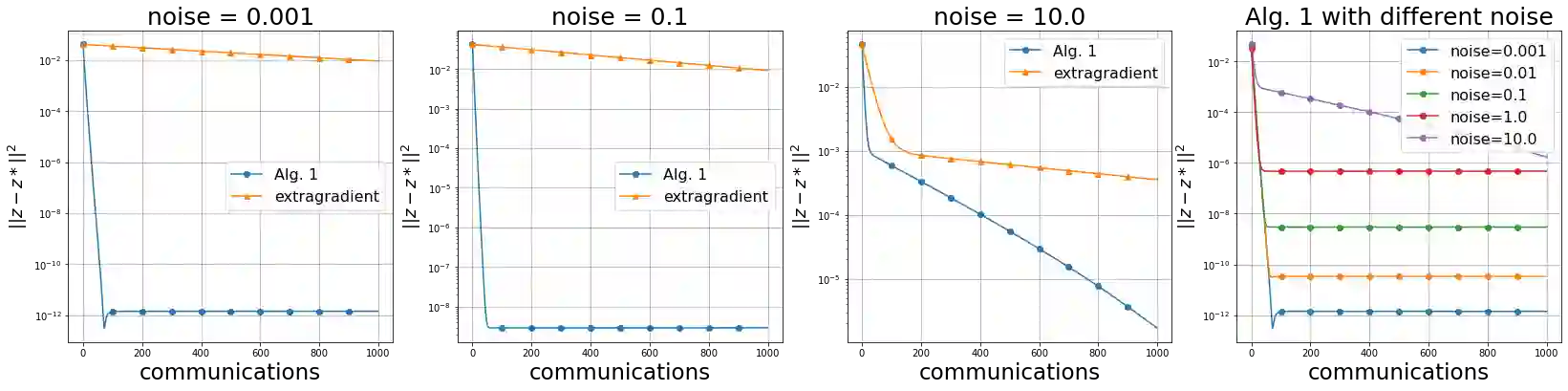
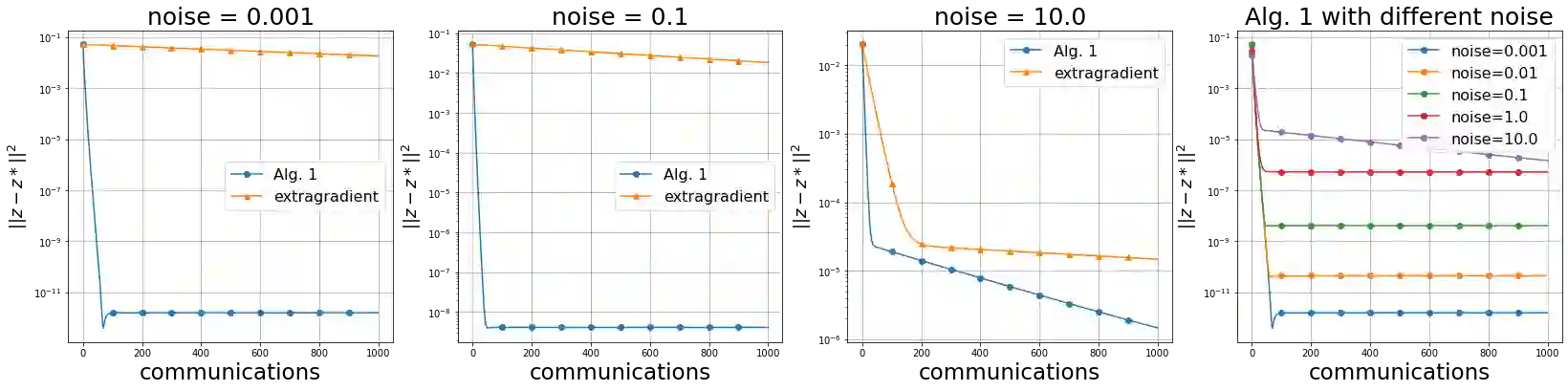
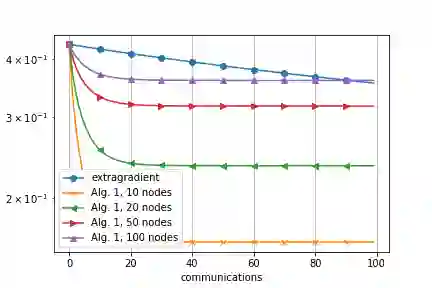
We study solution methods for (strongly-)convex-(strongly)-concave Saddle-Point Problems (SPPs) over networks of two type - master/workers (thus centralized) architectures and meshed (thus decentralized) networks. The local functions at each node are assumed to be similar, due to statistical data similarity or otherwise. We establish lower complexity bounds for a fairly general class of algorithms solving the SPP. We show that a given suboptimality $\epsilon>0$ is achieved over master/workers networks in $\Omega\big(\Delta\cdot \delta/\mu\cdot \log (1/\varepsilon)\big)$ rounds of communications, where $\delta>0$ measures the degree of similarity of the local functions, $\mu$ is their strong convexity constant, and $\Delta$ is the diameter of the network. The lower communication complexity bound over meshed networks reads $\Omega\big(1/{\sqrt{\rho}} \cdot {\delta}/{\mu}\cdot\log (1/\varepsilon)\big)$, where $\rho$ is the (normalized) eigengap of the gossip matrix used for the communication between neighbouring nodes. We then propose algorithms matching the lower bounds over either types of networks (up to log-factors). We assess the effectiveness of the proposed algorithms on a robust logistic regression problem.
翻译:我们研究两种类型网络的(强力) convex-(强力) conculex- concape-podle sadles (SPPs) 的解决方案方法。 由于统计数据相似或其他原因, 我们每个节点的本地功能假定相似。 我们为相当普通的解决 SPP 的算法类别设定了较低的复杂度。 我们显示, $\ epsilon > 0 的给定亚最佳度( Delta\ cdot ) 的主/ 工作网络在 $\ OmegaBig (Delta/ mum\ cdot) 的 Madel- host 结构架构和 mished (1/\ vareplusl) 网络中, $delepreta>0 用于测量本地函数相似度的幅度, $mutreglemental degility, $\\\\ delta$是网络的直径直径。 commetrefer coms rual rual rol roup roup roup $\ weqrmax (1\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ dislislislisl) romax romax rolup roma romax roma roma romax romax romax romax ro) romax roup roma roma romax roup ro) ro) ro) roup roup roup roc) rout ro) romax roc) roc) roc) rocl romabs romas a___ roma roma roclups romax romax rocl roma roma roma roma ro ro ro ro romas roma romas rocl roclup rocl rocl rocl rocl ro ro