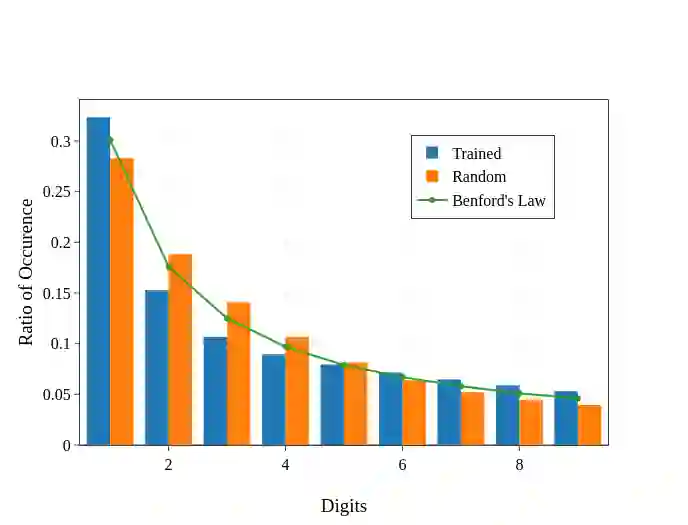
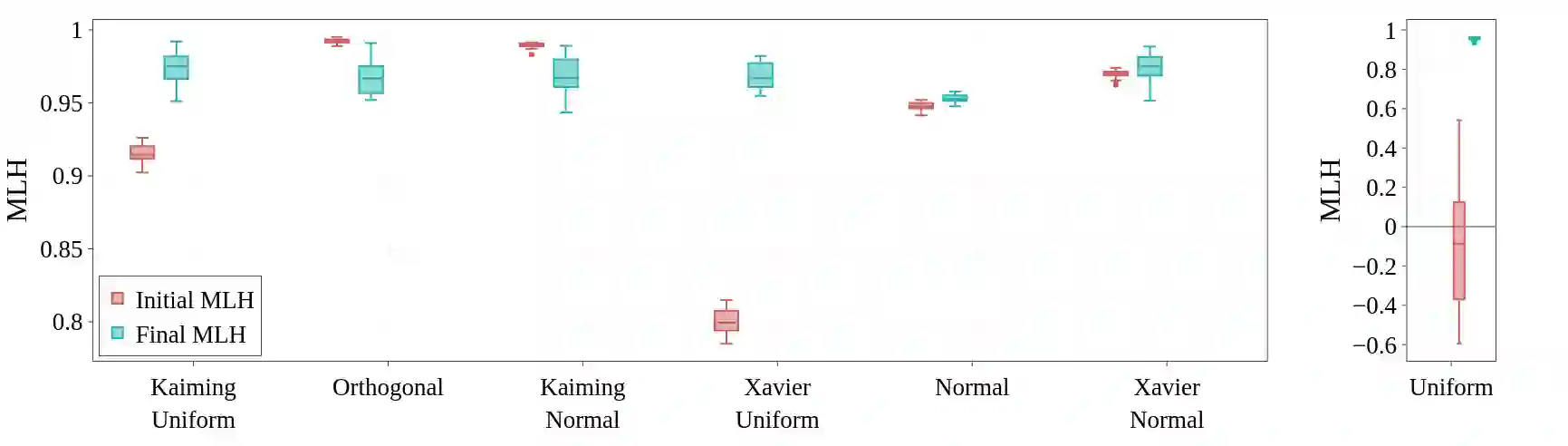
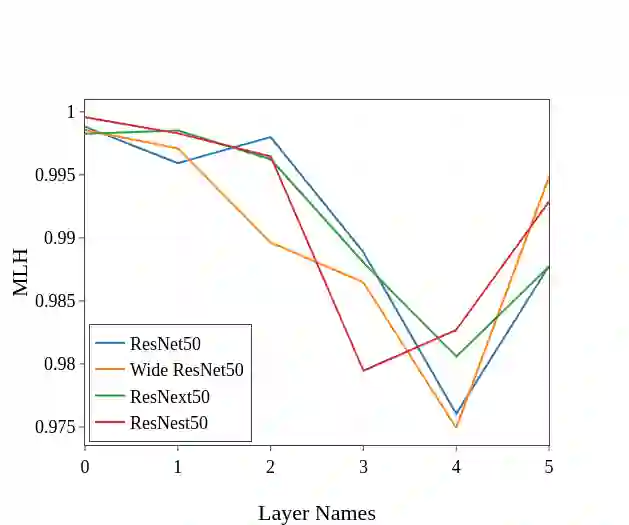
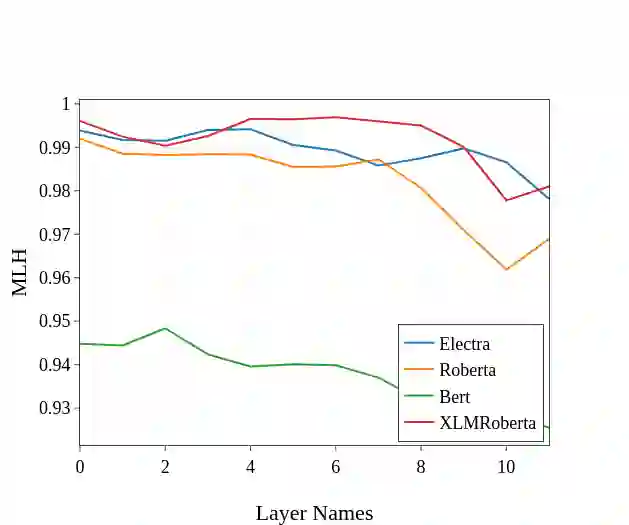
Benford's law, also called Significant Digit Law, is observed in many naturally occurring data-sets. For instance, the physical constants such as Gravitational, Coulomb's Constant, etc., follow this law. In this paper, we define a score, $MLH$, for how closely a Neural Network's Weights match Benford's law. We show that Neural Network Weights follow Benford's Law regardless of the initialization method. We make a striking connection between Generalization and the $MLH$ of the network. We provide evidence that several architectures from AlexNet to ResNeXt trained on ImageNet, Transformers (BERT, Electra, etc.), and other pre-trained models on a wide variety of tasks have a strong correlation between their test performance and the $MLH$. We also investigate the influence of Data in the Weights to explain why NNs possibly follow Benford's Law. With repeated experiments on multiple datasets using MLPs, CNNs, and LSTMs, we provide empirical evidence that there is a connection between $MLH$ while training, overfitting. Understanding this connection between Benford's Law and Neural Networks promises a better comprehension of the latter.
翻译:Benford 的法律, 也称为“ 重大数字法 ”, 在许多自然发生的数据集中都可以看到。 例如, 物理常数, 如重力、 库伦普的常数等, 都遵循此法。 在本文中, 我们定义了一个分数, $MLH$, 用于神经网络的重量与本福特的法律之间的关系。 我们还调查了数据在 Weights 中的影响, 以解释为什么NUS 可能遵循本福德的法律。 我们用MLP、 CNN 和 LSTMS 反复对多个数据集进行了实验。 我们提供证据表明, 从AlexNet到ResNeXt 在图像网络、变换器(BERT、Lectra等)上受过训练的几个建筑, 以及其他经过预先训练的任务种类广泛的模型, 它们的测试性能和美元与BenMLH$H 之间有很强的关联性关系。 我们还调查了数据在Weights 中的影响, 解释为什么NUS 可能遵循本福德法律。 我们反复用MLPs、 和LSTMMMMS, 我们提供了实验性证据表明, 在Binalforlation之间有更好的理解 。