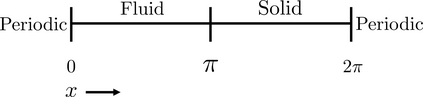
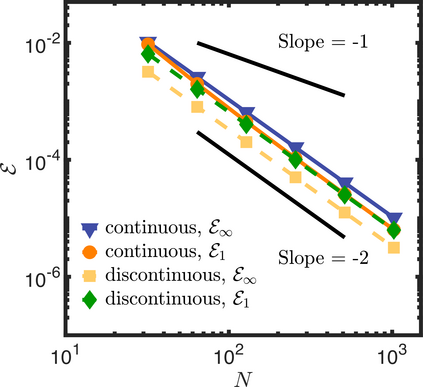
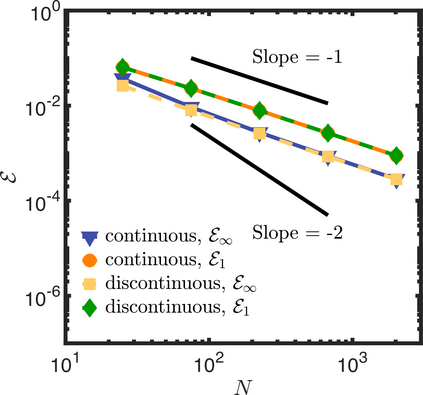
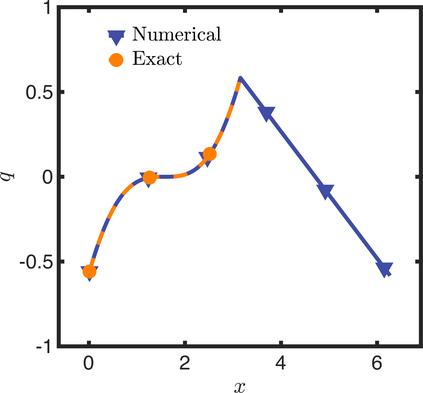
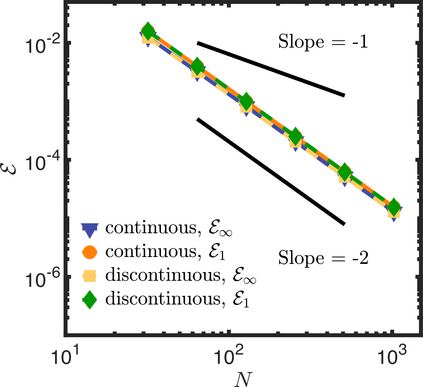
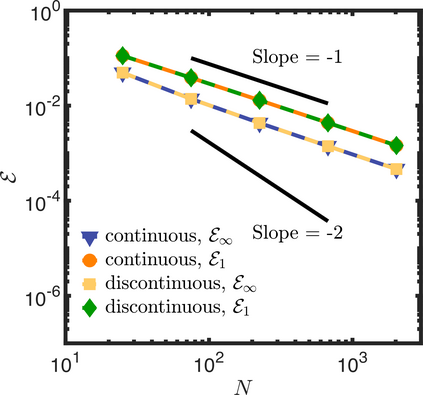
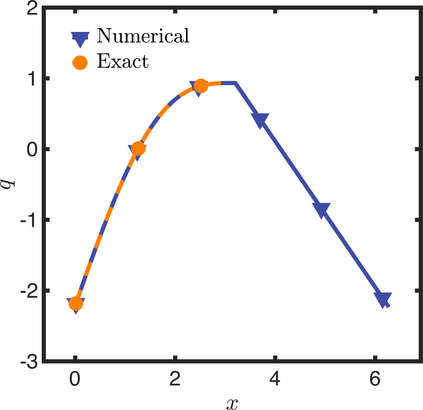
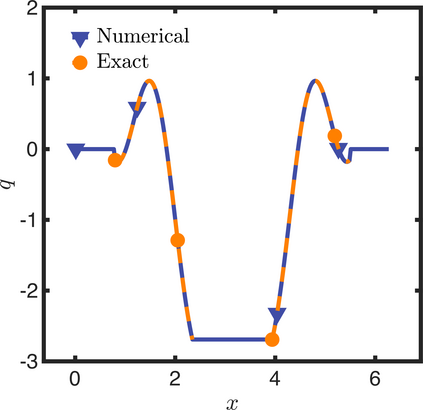
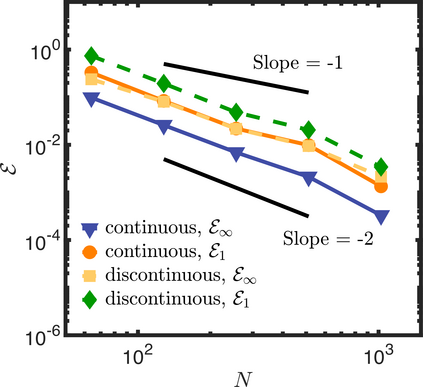
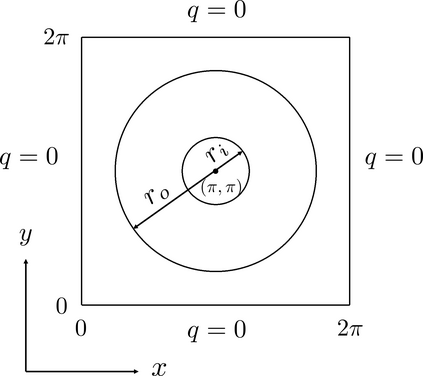
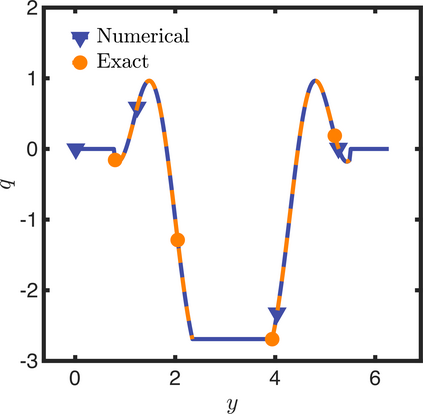
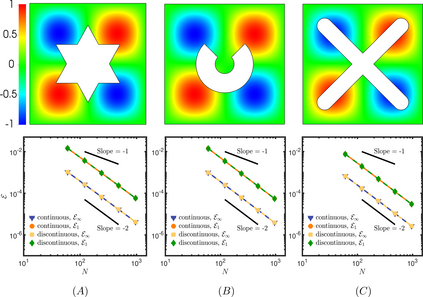
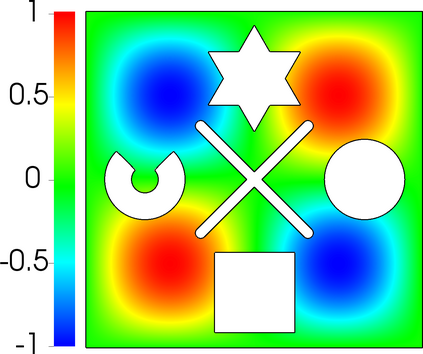
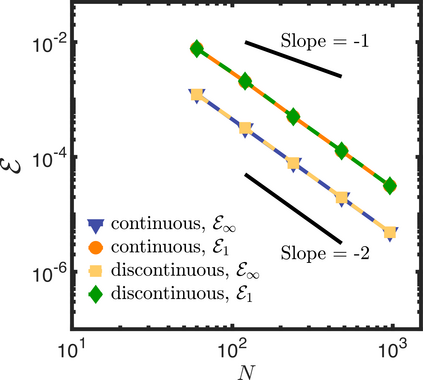
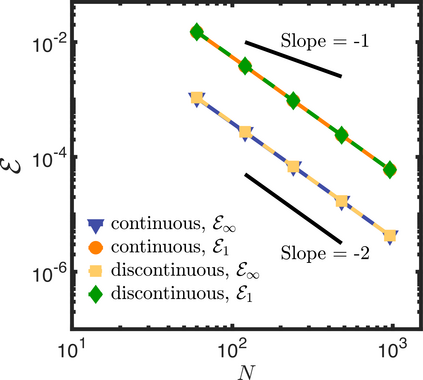
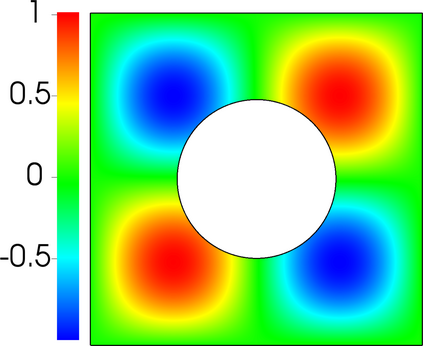
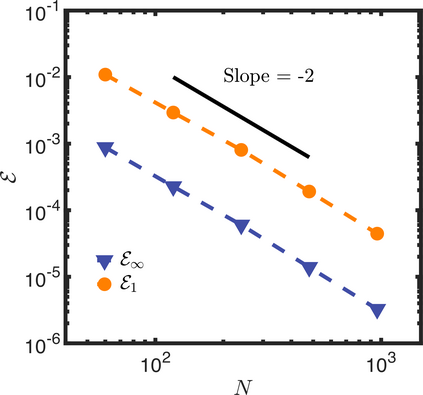
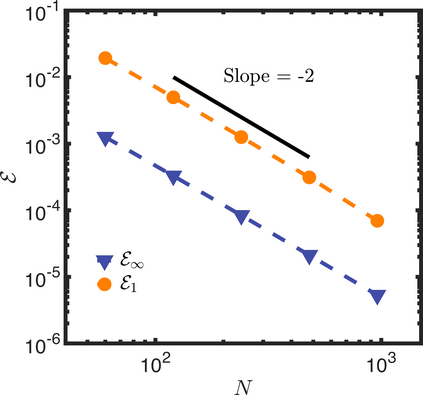
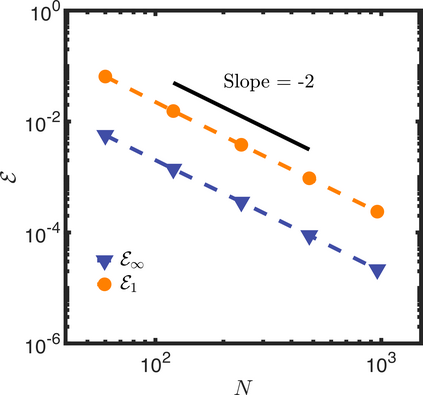
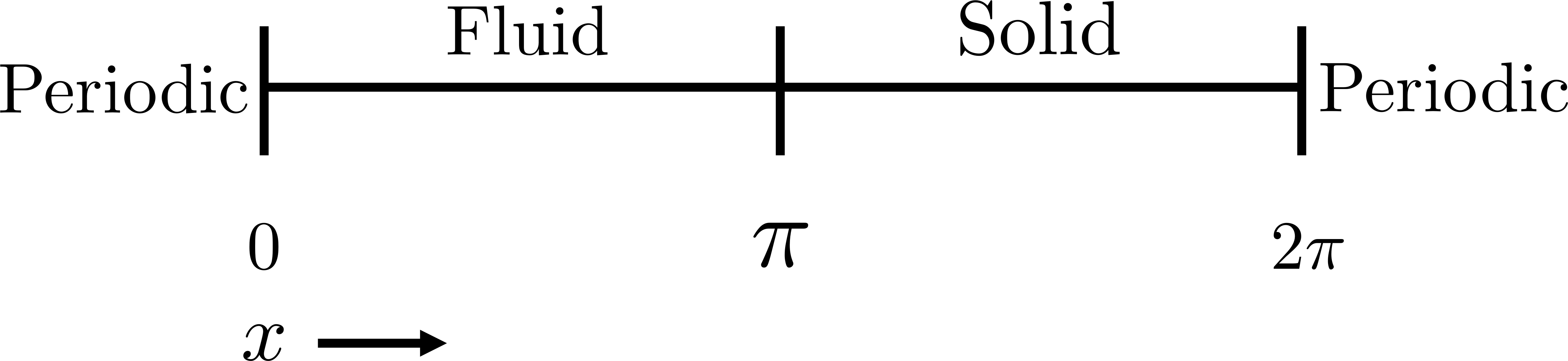
In this letter, we provide counter-examples to demonstrate that it is possible to retain second-order accuracy using Sakurai et al.'s method, even when different flux boundary conditions are imposed on multiple interfaces that do not conform to the Cartesian grid. We consider both continuous and discontinuous indicator functions in our test problems. Both indicator functions yield a similar convergence rate for the problems considered here. We also find that the order of accuracy results for some of the cases presented in Sakurai et al. are not reproducible. This is demonstrated by re-considering the same one- and two-dimensional Poisson problems solved in Sakurai et al. in this letter. The results shown in this letter demonstrate that the spatial order of accuracy of the flux-based VP approach of Sakurai et al. is between $\mathcal{O}$(1) and $\mathcal{O}$(2), and it depends on the underlying problem/model. The spatial order of accuracy cannot simply be deduced a priori based on the imposed flux values, shapes, or grid-conformity of the interfaces, as concluded in Sakurai et al. Further analysis is required to understand the spatial convergence rate of the flux-based VP method.
翻译:在本信中,我们提供了反抽样,以证明有可能使用Sakurai等人的方法保留二阶精确度,即使对不符合笛卡尔网格的多个界面规定了不同的通量边界条件,我们也考虑连续和不连续的指标功能。我们考虑测试问题中的连续和不连续指标功能。两个指标函数对这里考虑的问题产生类似的趋同率。我们还发现,Sakurai等人提出的某些案例的准确性结果顺序无法再复制。本信对Sakurai等人解决的同一一维和二维Poisson问题进行重新思考就证明了这一点。本信中显示的结果表明,Sakurai等人基于通量的VP方法的准确性空间顺序在$\mascal{O}(1)和$\mathcal{O}(2)之间,这取决于根本问题/模式。根据强加的通量值、形状或界面的电格化性,无法简单地根据Sakurai等的先前推算出准确度。根据Sakura等人的通量值、形状或电解度分析,进一步理解Sakura等人的通量分析中所需的V-qura 等方法所需的空间趋同率。