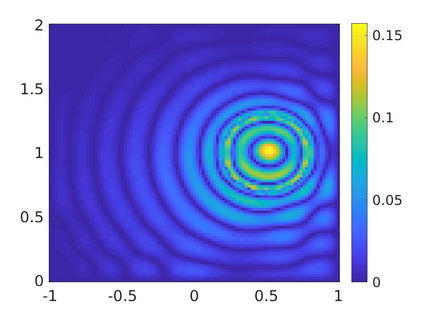
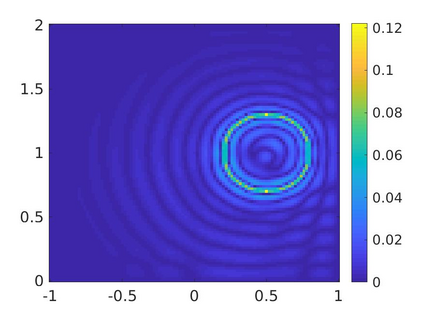
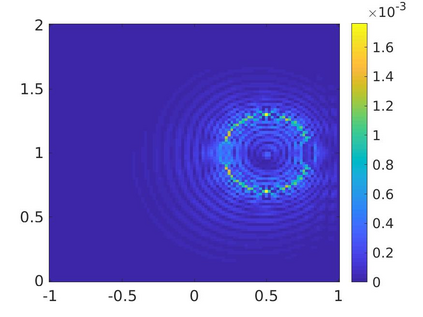
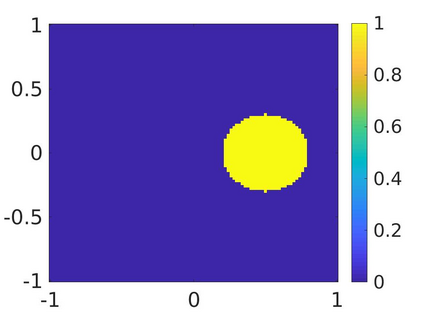
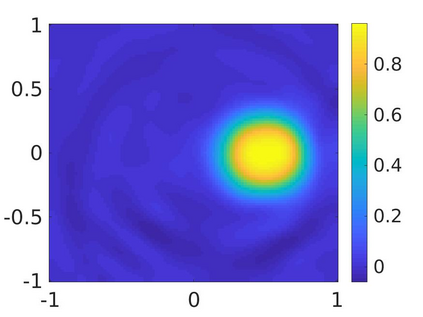
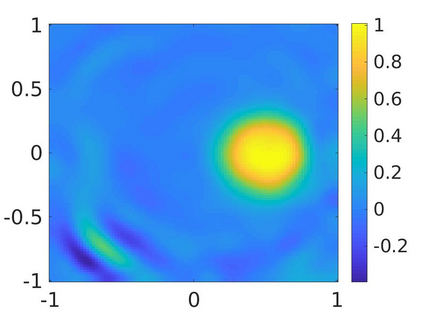
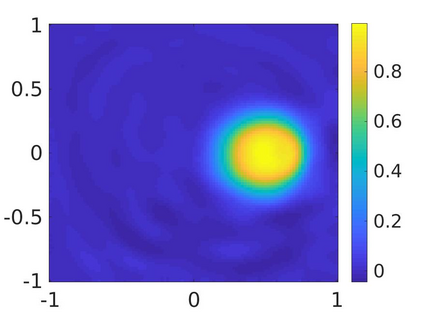
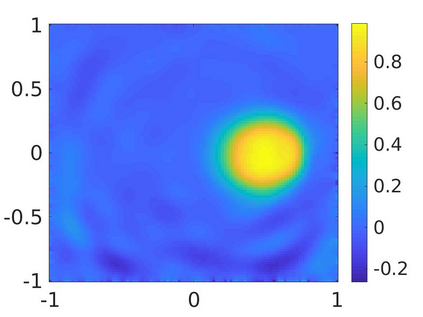
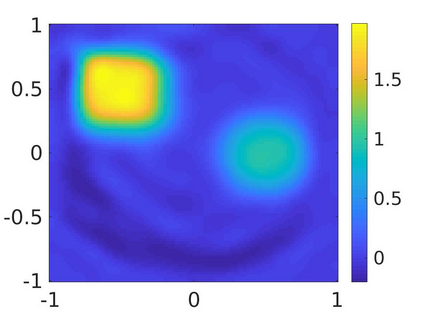
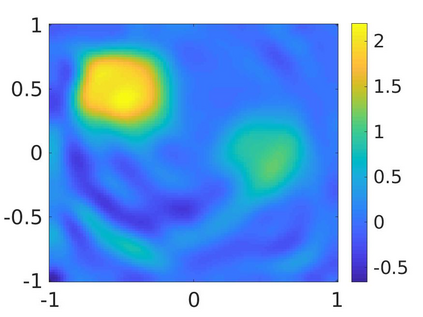
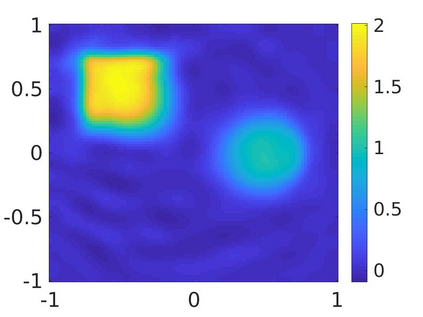
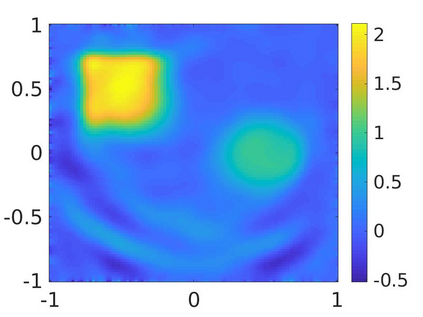
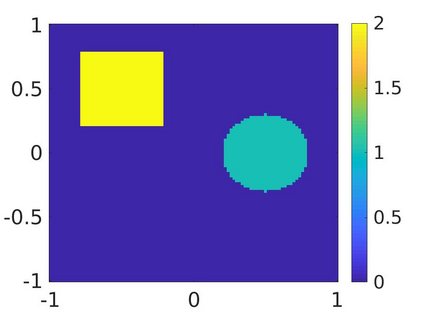
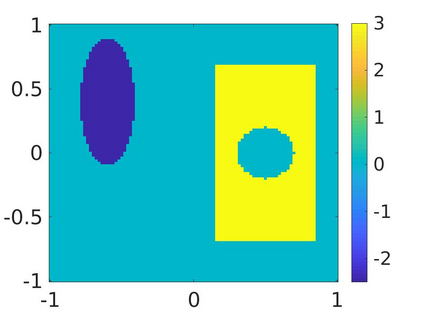
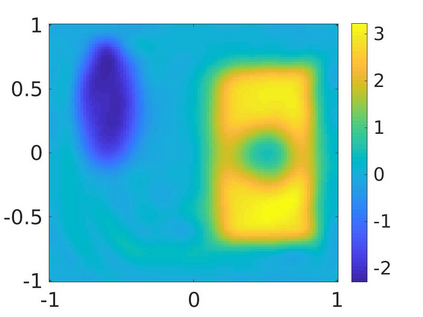
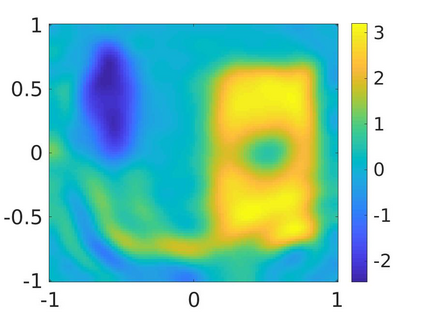
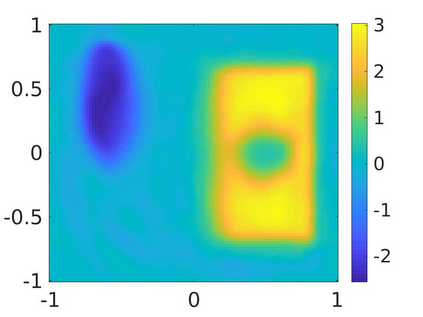
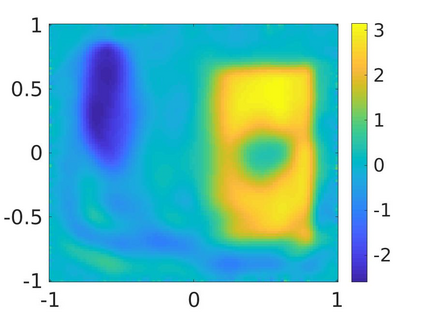
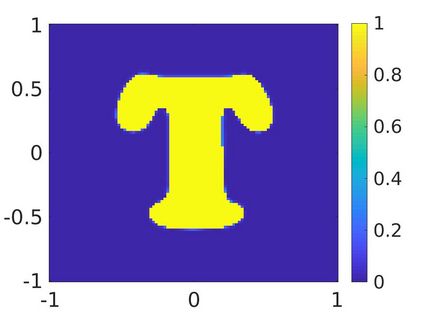
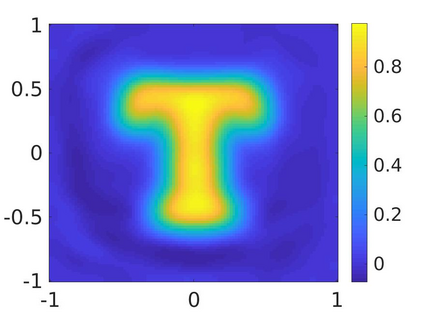
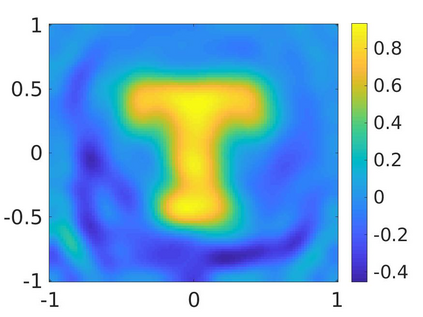
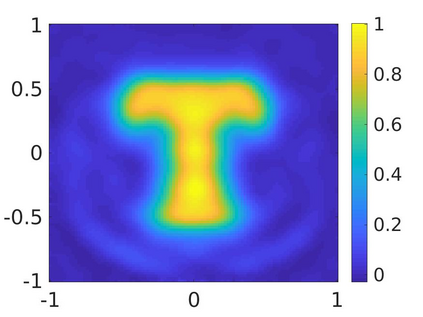
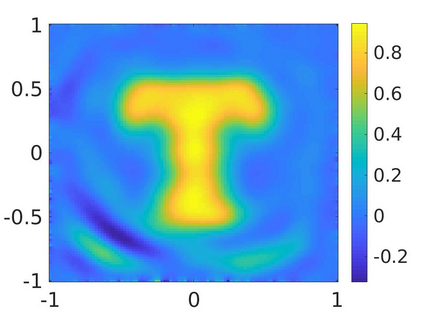
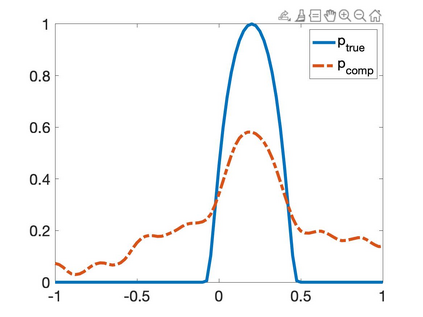
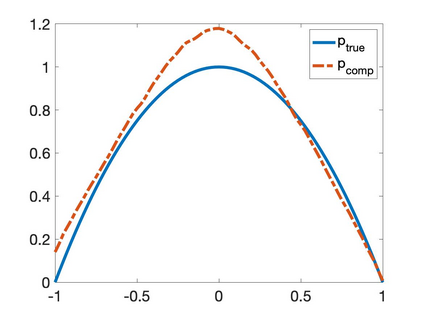
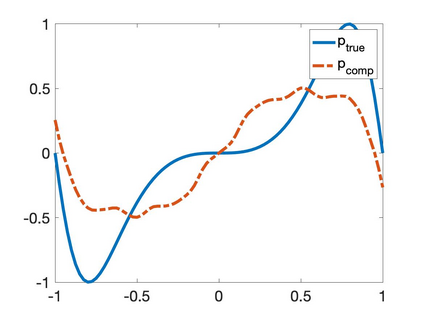
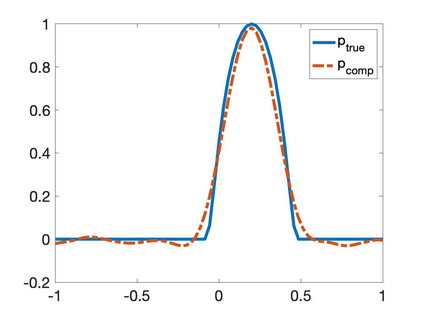
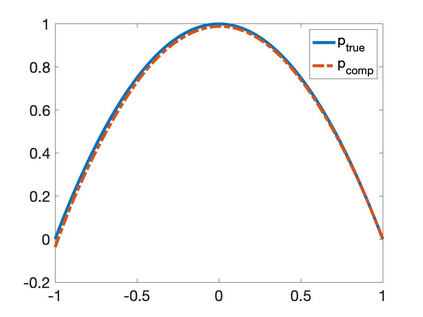
We propose a numerical method to solve an inverse source problem of computing the initial condition of hyperbolic equations from the measurements of Cauchy data. This problem arises in thermo- and photo- acoustic tomography in a bounded cavity, in which the reflection of the wave makes the widely-used approaches, such as the time reversal method, not applicable. In order to solve this inverse source problem, we approximate the solution to the hyperbolic equation by its Fourier series with respect to a special orthogonal basis of $L^2$. Then, we derive a coupled system of elliptic equations for the corresponding Fourier coefficients. We solve it by the quasi-reversibility method. The desired initial condition follows. We rigorously prove the convergence of the quasi-reversibility method as the noise level tends to 0. Some numerical examples are provided. In addition, we numerically prove that the use of the special basic above is significant.
翻译:我们建议了一个数字方法来解决从测量Cauchy数据中计算双曲方程式初始状态的反源问题。 这个问题出现在一个封闭的洞穴中的热声和光声断声仪中, 其中波的反射使得广泛使用的方法, 如时间倒转方法, 并不适用。 为了解决这一反源问题, 我们用它的Fourier系列来比较对双曲方程式的解决方案, 其特殊正方圆基值为$L ⁇ 2美元。 然后, 我们为相应的 Fourier 系数生成一个混合的椭圆方程系统。 我们用准反转性方法解决这个问题。 理想的初始条件是随后。 我们严格地证明准反转法的趋同性方法, 因为噪音水平一般为0。 提供了一些数字实例。 此外, 我们用数字来证明上述特殊基本系数的使用很重要。