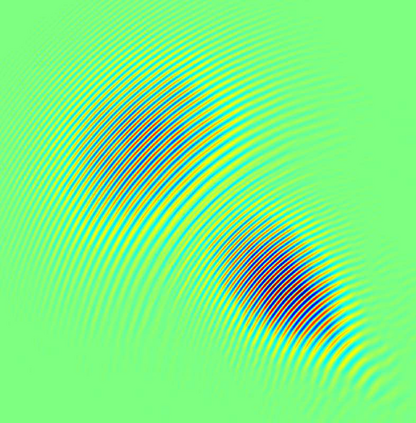
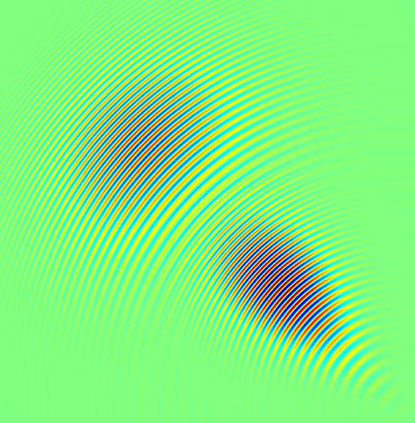
In this article, we introduce the frozen Gaussian sampling (FGS) algorithm to solve the scalar wave equation in the high-frequency regime. The FGS algorithm is a Monte Carlo sampling strategy based on the frozen Gaussian approximation, which greatly reduces the computation workload in the wave propagation and reconstruction. In this work, we propose feasible and detailed procedures to implement the FGS algorithm to approximate scalar wave equations with Gaussian initial conditions and WKB initial conditions respectively. For both initial data cases, we rigorously analyze the error of applying this algorithm to wave equations of dimensionality $d \geq 3$. In Gaussian initial data cases, we prove that the sampling error due to the Monte Carlo method is independent of the typical wave number. We also derive a quantitative bound of the sampling error in WKB initial data cases. Finally, we validate the performance of the FGS and the theoretical estimates about the sampling error through various numerical examples, which include using the FGS to solve wave equations with both Gaussian and WKB initial data of dimensionality $d = 1, 2$, and $3$.
翻译:在本篇文章中,我们引入了冻结的高斯取样算法(FGS), 以解决高频系统中的斜波方程式。 FGS 算法是一种基于冻结的高斯近似值的蒙特卡洛取样战略, 大大降低了波传播和重建过程中的计算工作量。 在这项工作中, 我们提出了实施FGS算法的可行和详细的程序, 以分别与高斯初始条件和WKB初始条件相近的斜波方程式相近。 对于这两个初始数据案例, 我们严格分析将这一算法应用于维度波方程式$d\geq 3美元的错误。 在高斯初步数据案例中, 我们证明因蒙特卡洛方法造成的取样错误独立于典型的波数数字。 我们还提出了WKB初始数据案例中取样错误的定量组合。 最后, 我们通过各种数字实例来验证 FGS的性能和取样错误的理论估计值, 其中包括使用高斯和WKB初始数据, 美元= 1, 2美元和3美元。