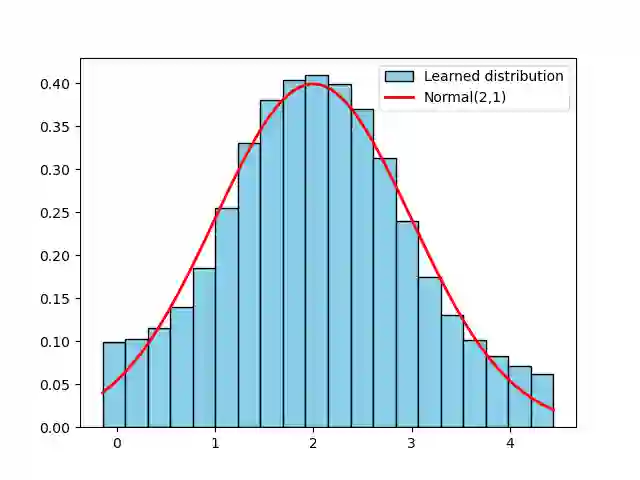
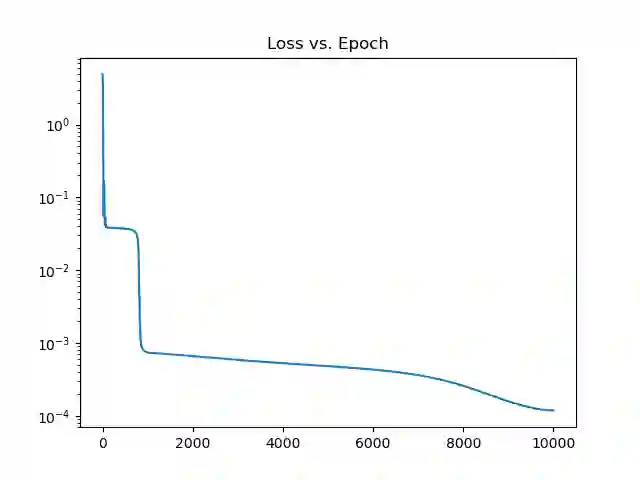
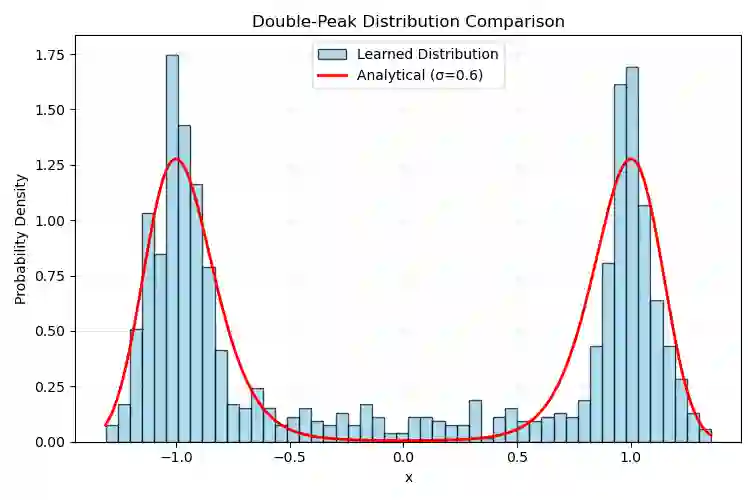
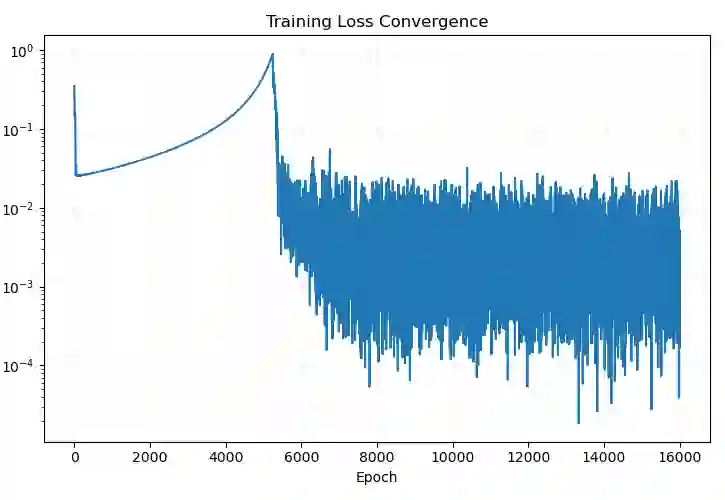
This paper presents a new method for solving Fokker-Planck equations (FPE) by learning a neural sampler for the distribution given by the FPE via an adversarial training based on a weak formulation of the FPE where the adjoint operator of FPE acts on the test function. Such a weak formulation transforms the PDE solution problem into a Monte Carlo importance sampling problem where the FPE solution-distribution is learned through a neural pushforward map, avoiding some of the limitations of direct PDE based methods. Moreover, by using simple plane-wave test functions, derivatives on the test functions can be explicitly computed. This approach produces a natural importance sampling strategy for the FPE solution distribution with probability conservation, from which the FPE solution can be easily constructed.
翻译:本文提出了一种求解福克-普朗克方程的新方法,该方法通过基于FPE弱形式的对抗训练来学习FPE所给分布的神经采样器,其中FPE的伴随算子作用于测试函数。这种弱形式将偏微分方程求解问题转化为蒙特卡洛重要性采样问题,通过神经前推映射学习FPE的解分布,从而规避了基于直接PDE方法的一些局限性。此外,通过使用简单的平面波测试函数,可以显式计算测试函数的导数。该方法为具有概率守恒性的FPE解分布生成了一种自然的重要性采样策略,从而可以轻松构建FPE的解。