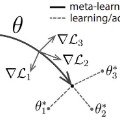
We study the personalized federated learning problem under asynchronous updates. In this problem, each client seeks to obtain a personalized model that simultaneously outperforms local and global models. We consider two optimization-based frameworks for personalization: (i) Model-Agnostic Meta-Learning (MAML) and (ii) Moreau Envelope (ME). MAML involves learning a joint model adapted for each client through fine-tuning, whereas ME requires a bi-level optimization problem with implicit gradients to enforce personalization via regularized losses. We focus on improving the scalability of personalized federated learning by removing the synchronous communication assumption. Moreover, we extend the studied function class by removing boundedness assumptions on the gradient norm. Our main technical contribution is a unified proof for asynchronous federated learning with bounded staleness that we apply to MAML and ME personalization frameworks. For the smooth and non-convex functions class, we show the convergence of our method to a first-order stationary point. We illustrate the performance of our method and its tolerance to staleness through experiments for classification tasks over heterogeneous datasets.
翻译:我们在非同步更新中研究个人化的联邦学习问题。 在这个问题中,每个客户都寻求获得一个个人化的模式,该模式同时优于本地和全球模式。我们考虑两个基于优化的个人化框架:(一) 模型-不可知元学习(MAML)和(二) Moreau Envelope (ME)。MAML 涉及通过微调学习适合每个客户的联合模式,而ME 则需要双级优化问题,即隐含的梯度,以通过正常化损失强制实现个人化。我们侧重于通过消除同步通信假设来改进个人化的联邦化学习的可扩展性。此外,我们通过去除梯度规范上的界限假设来扩展所研究的功能类。我们的主要技术贡献是统一证明我们适用于MAML和ME 个化框架的无节点。对于平滑和非凝固函数类,我们展示了我们的方法与第一个顺序固定点的趋同。我们的方法的性表现及其通过对数据分类的实验来容忍性。