Towards end-to-end ASP computation

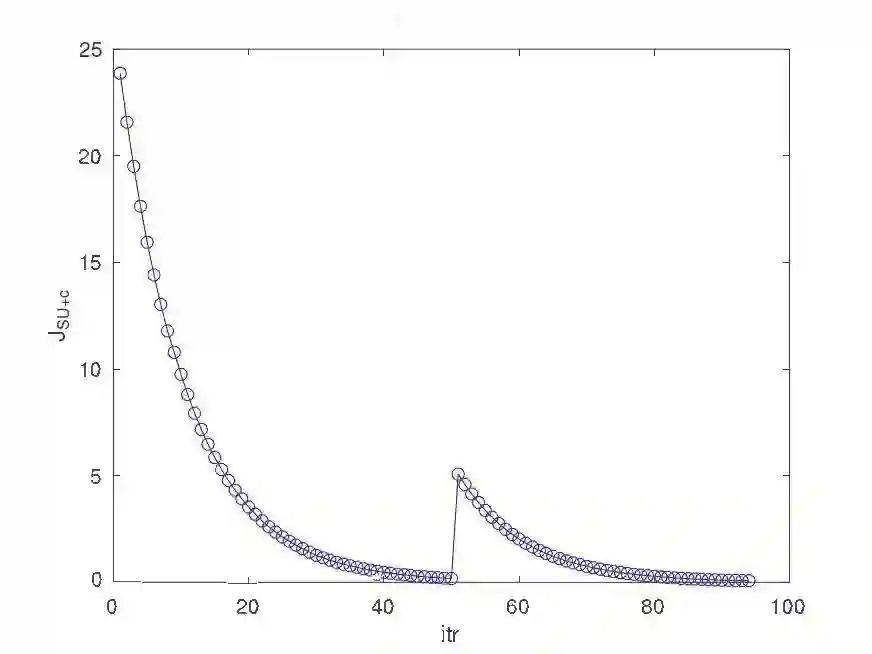
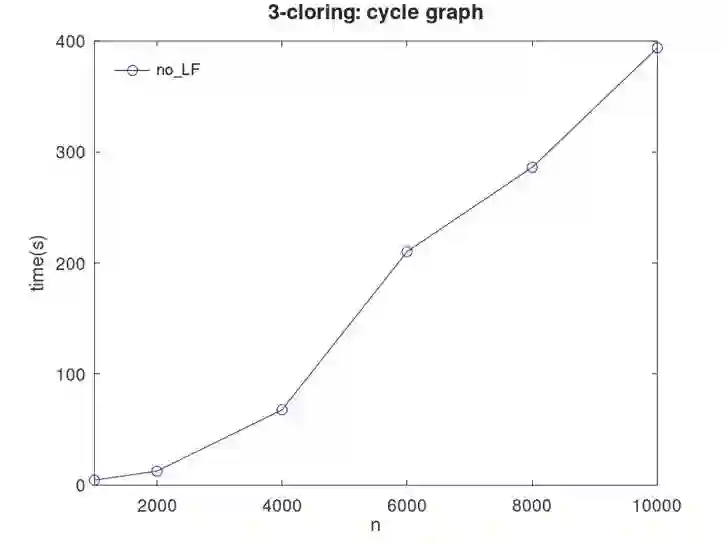
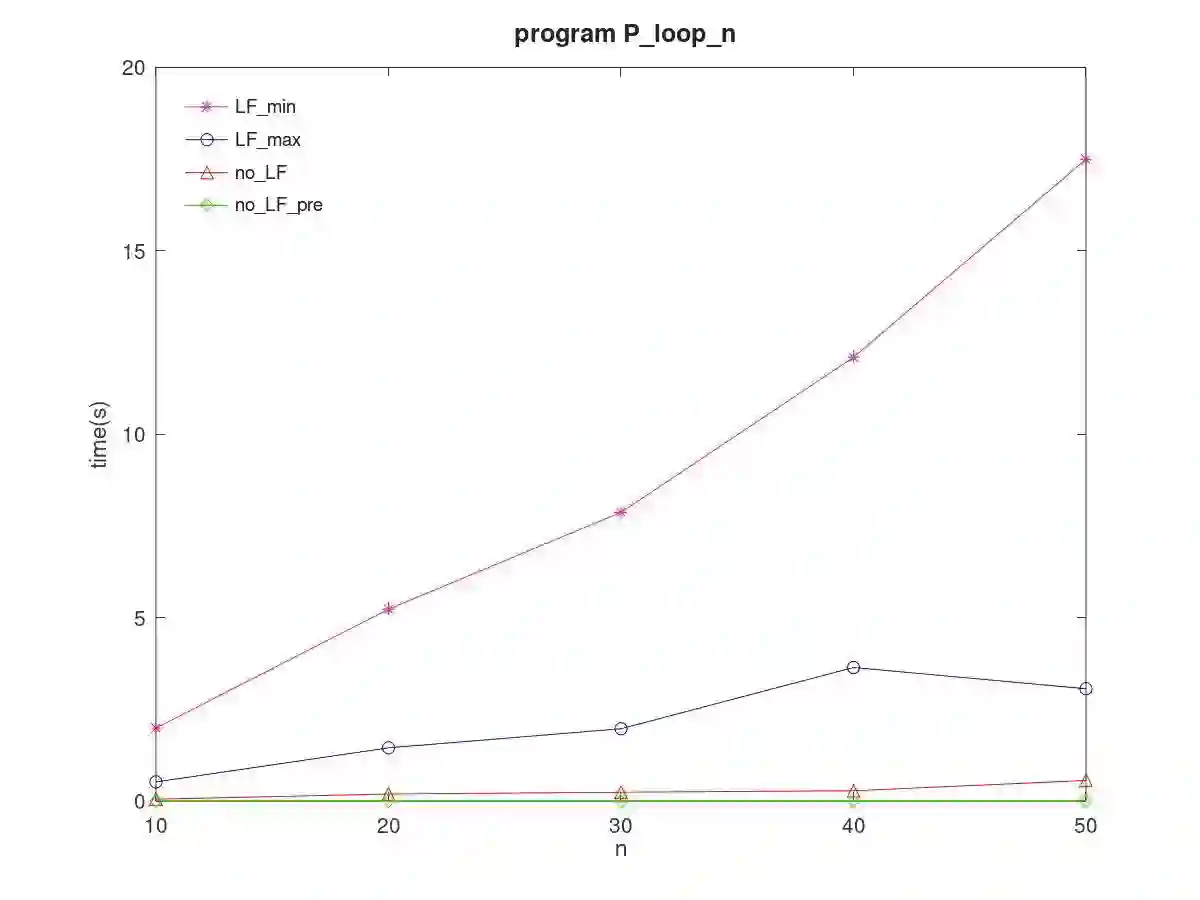
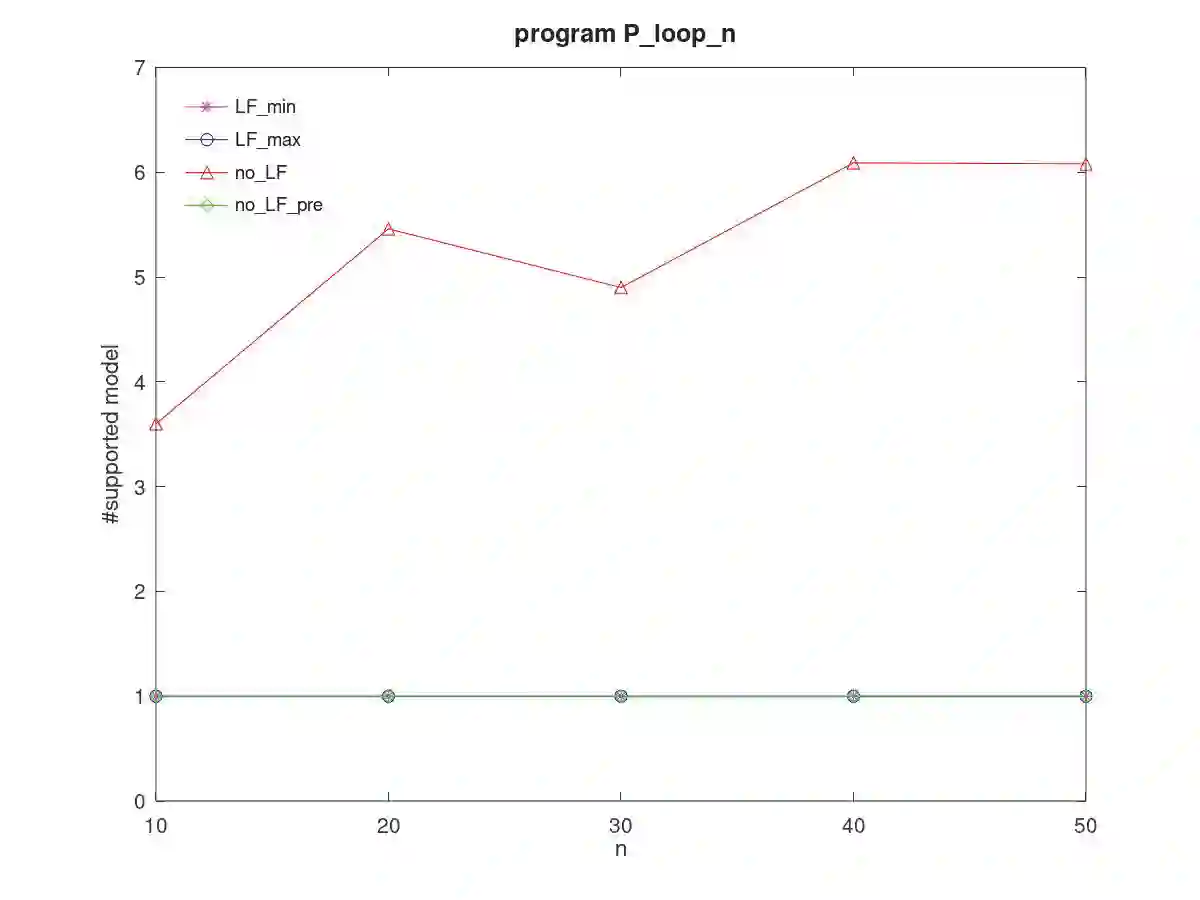
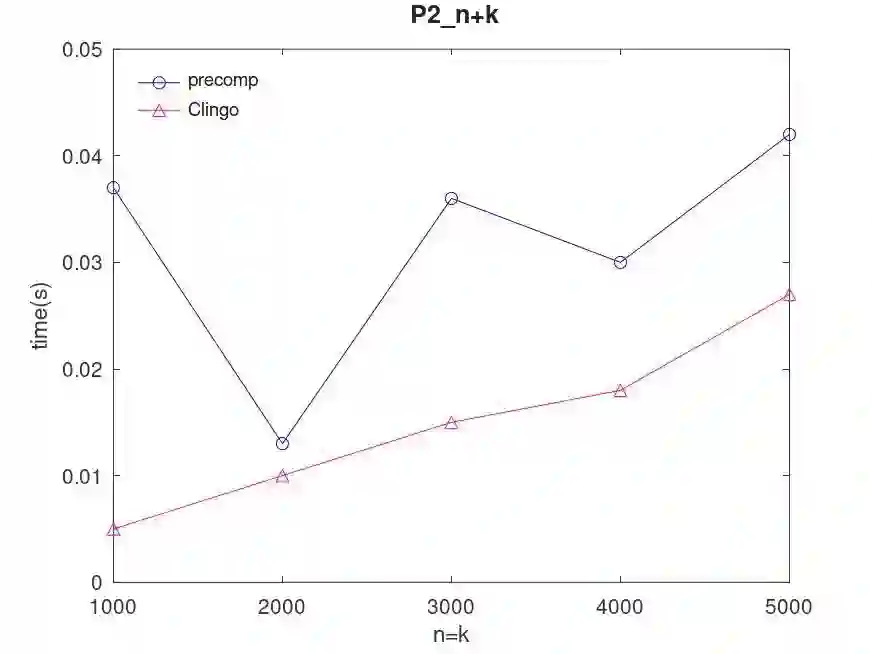
We propose an end-to-end approach for Answer Set Programming (ASP) and linear algebraically compute stable models satisfying given constraints. The idea is to implement Lin-Zhao's theorem together with constraints directly in vector spaces as numerical minimization of a cost function constructed from a matricized normal logic program, loop formulas in Lin-Zhao's theorem and constraints, thereby no use of symbolic ASP or SAT solvers involved in our approach. We also propose precomputation that shrinks the program size and heuristics for loop formulas to reduce computational difficulty. We empirically test our approach with programming examples including the 3-coloring and Hamiltonian cycle problems.