Parameter estimation for many-particle models from aggregate observations: A Wasserstein distance based sequential Monte Carlo sampler

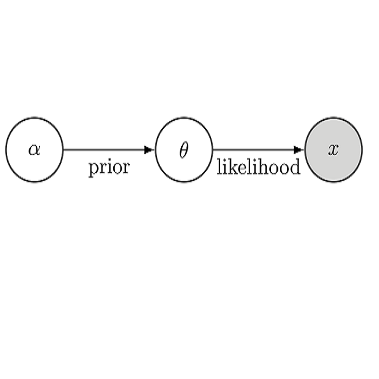
In this work we study systems consisting of a group of moving particles. In such systems, often some important parameters are unknown and have to be estimated from observed data. Such parameter estimation problems can often be solved via a Bayesian inference framework. However in many practical problems, only data at the aggregate level is available and as a result the likelihood function is not available, which poses challenge for Bayesian methods. In particular, we consider the situation where the distributions of the particles are observed. We propose a Wasserstein distance based sequential Monte Carlo sampler to solve the problem: the Wasserstein distance is used to measure the similarity between the observed and the simulated particle distributions and the sequential Monte Carlo samplers is used to deal with the sequentially available observations. Two real-world examples are provided to demonstrate the performance of the proposed method.