Isogeometric discretizations of the Stokes problem on trimmed geometries

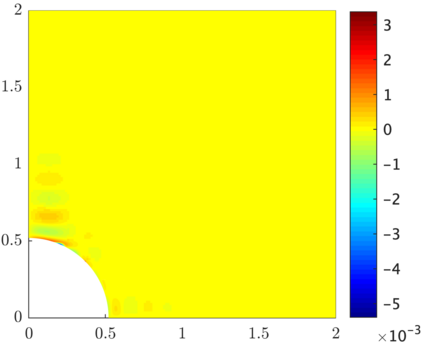
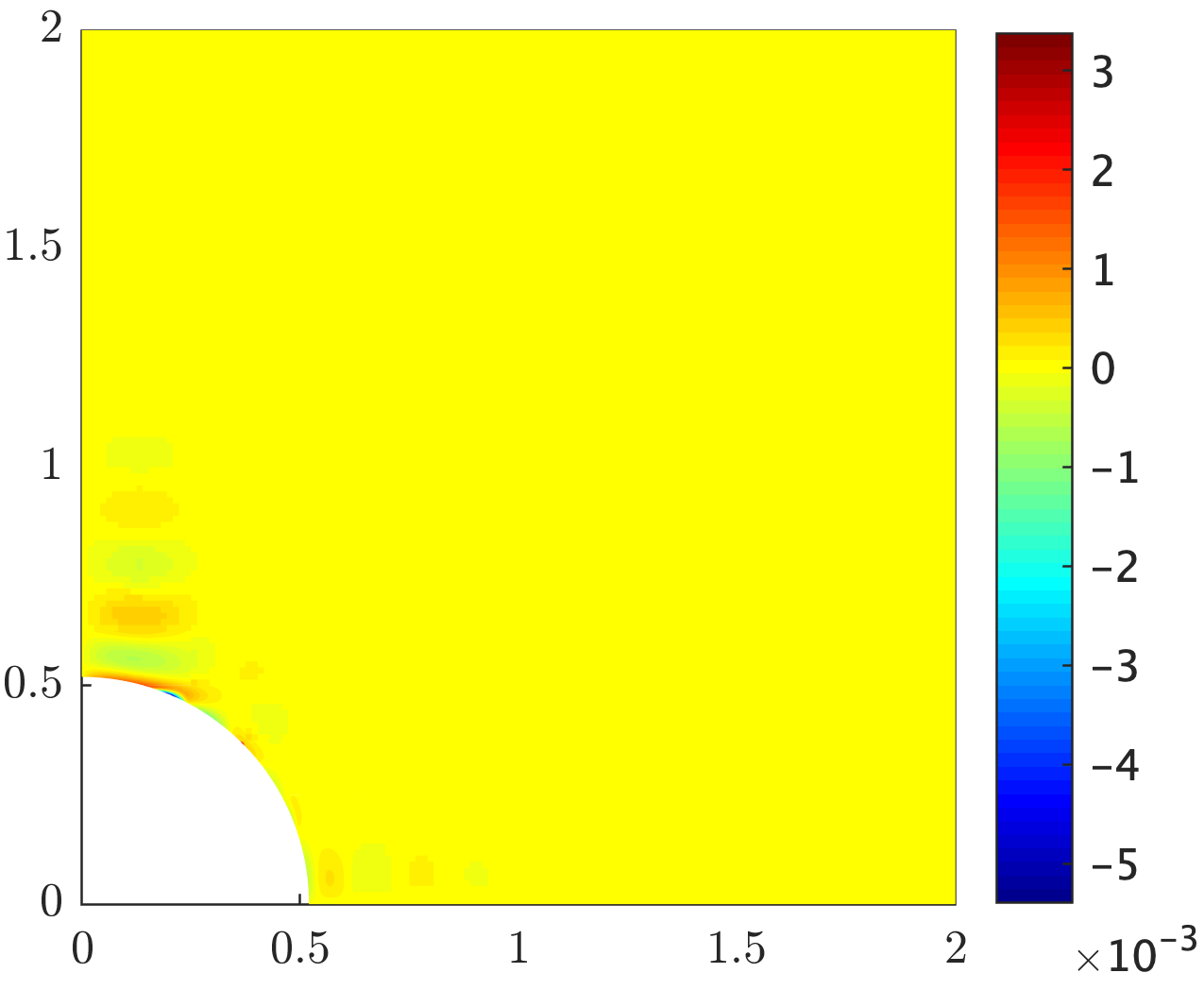
The isogeometric approximation of the Stokes problem in a trimmed domain is studied. This setting is characterized by an underlying mesh unfitted with the boundary of the physical domain making the imposition of the essential boundary conditions a challenging problem. A very popular strategy is to rely on the so-called Nitsche method [22]. We show with numerically examples that in some degenerate trimmed domain configurations there is a lack of stability of the formulation, potentially polluting the computed solutions. After extending the stabilization procedure of [17] to incompressible flow problems, we theoretically prove that, combined with the Raviart-Thomas isogeometric element, we are able to recover the well-posedness of the formulation and, consequently, optimal a priori error estimates. Numerical results corroborating the theory and extending it for the case of the isogeometric N\'ed\'elec and Taylor-Hood elements are provided.