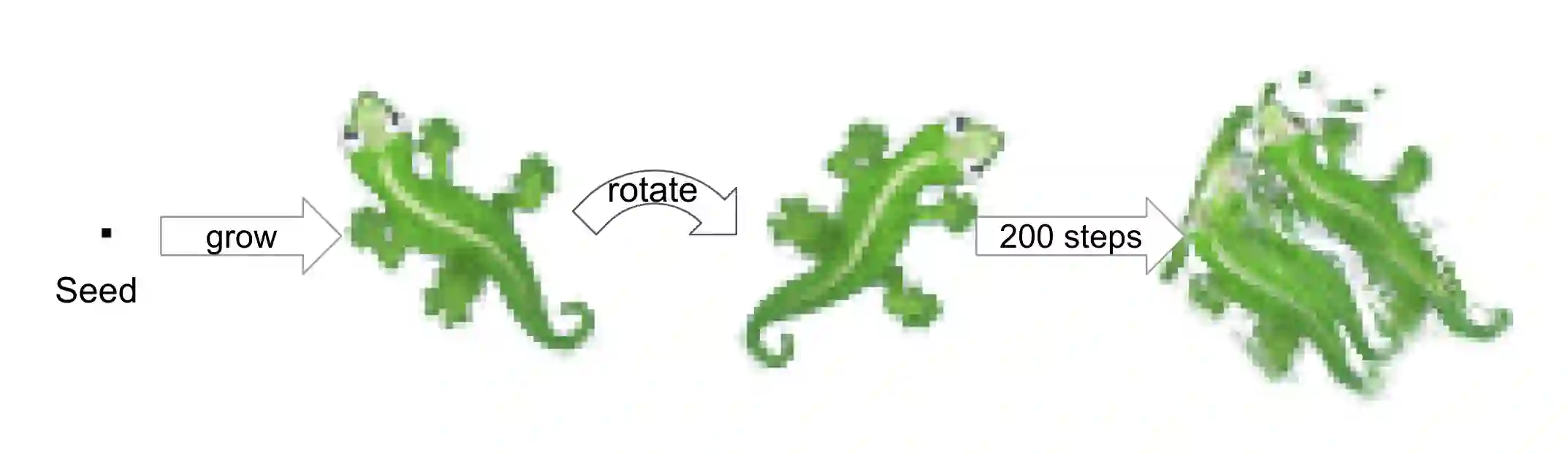
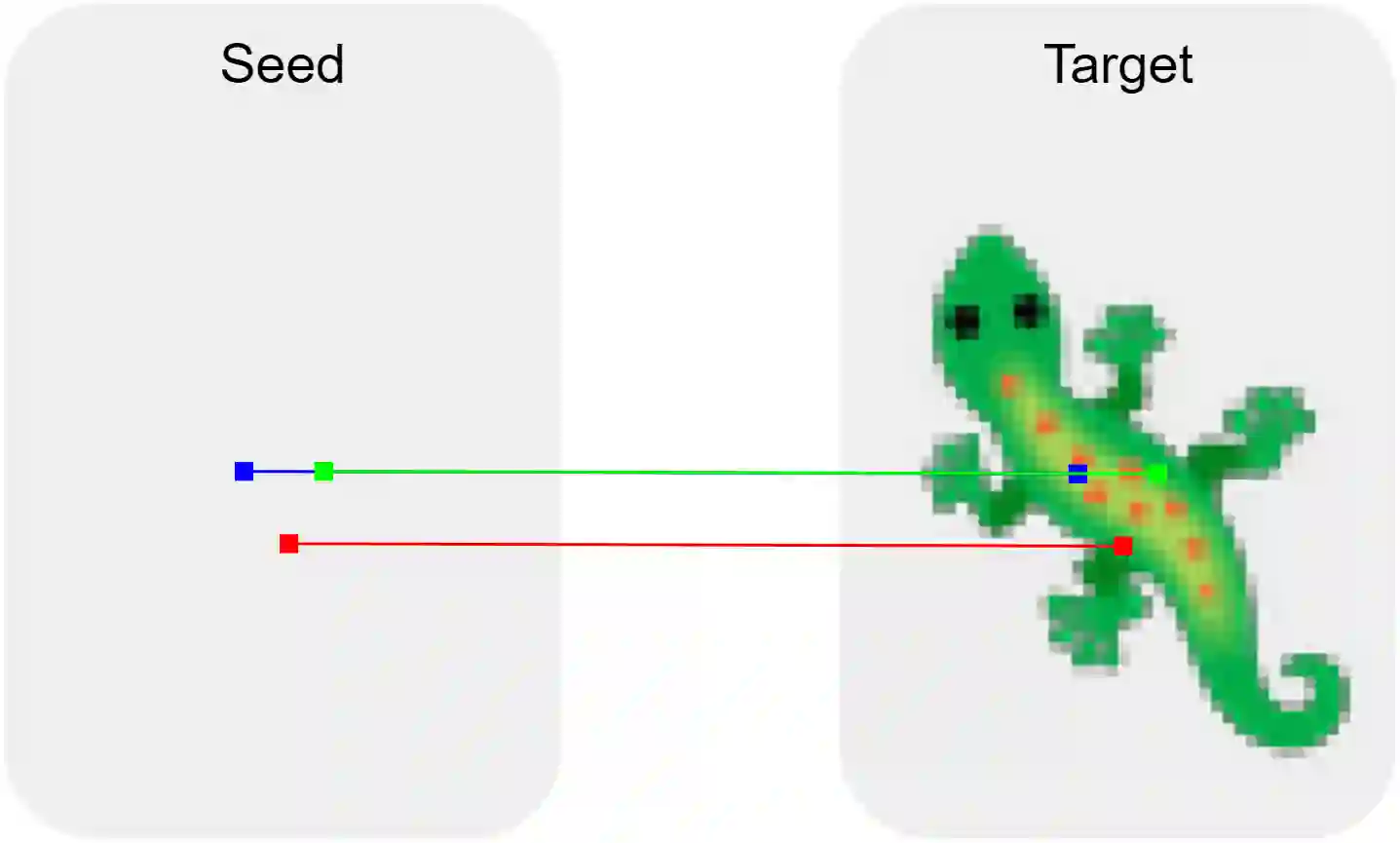
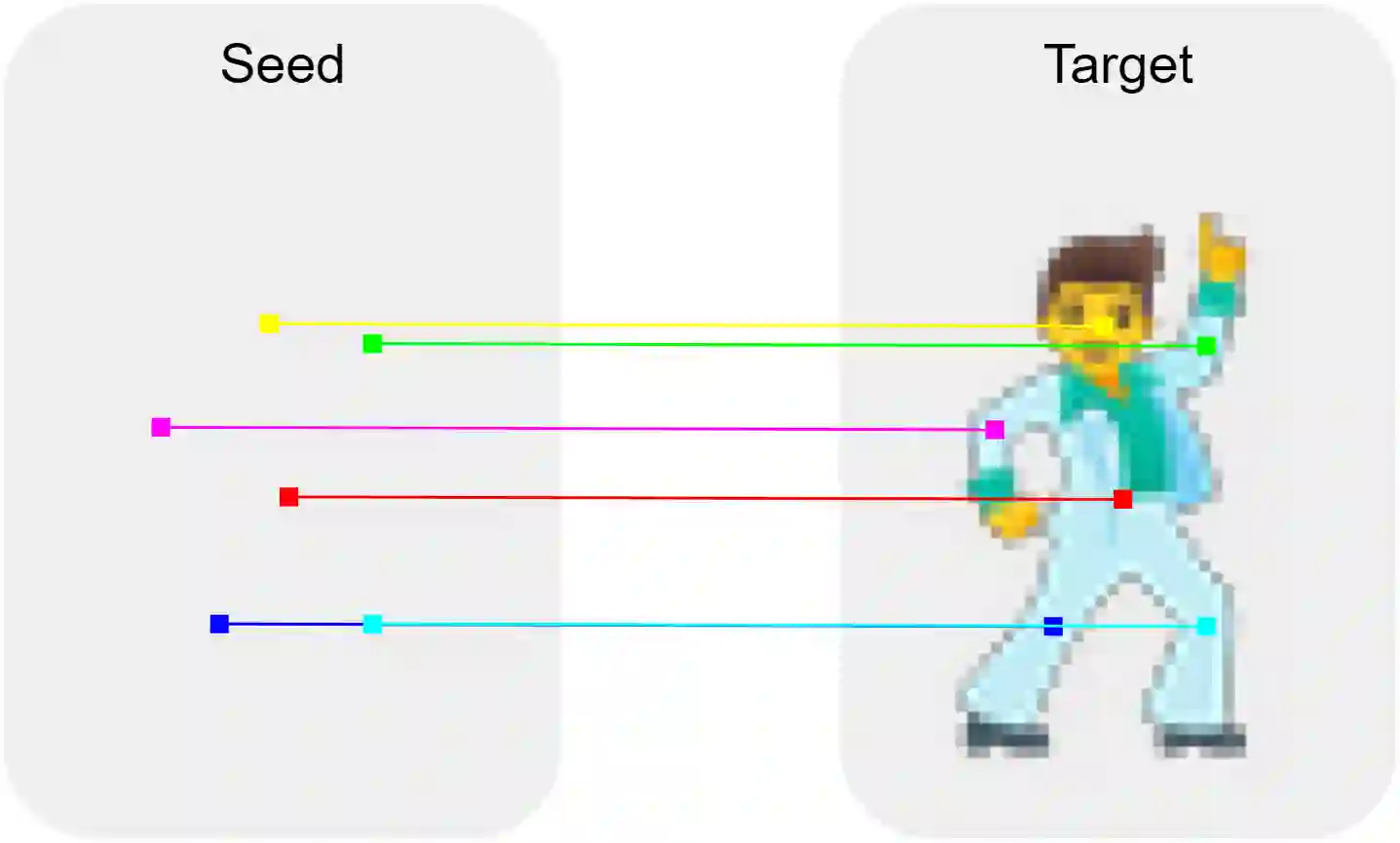
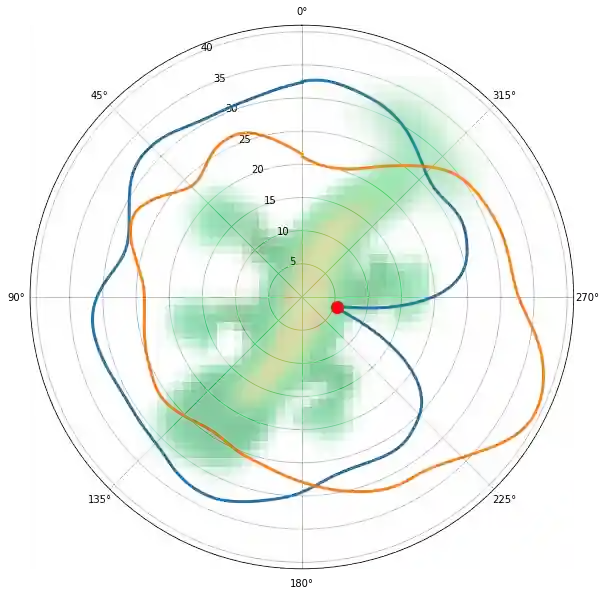
Modeling the ability of multicellular organisms to build and maintain their bodies through local interactions between individual cells (morphogenesis) is a long-standing challenge of developmental biology. Recently, the Neural Cellular Automata (NCA) model was proposed as a way to find local system rules that produce a desired global behaviour, such as growing and persisting a predefined target pattern, by repeatedly applying the same rule over a grid starting from a single cell. In this work, we argue that the original Growing NCA model has an important limitation: anisotropy of the learned update rule. This implies the presence of an external factor that orients the cells in a particular direction. In other words, "physical" rules of the underlying system are not invariant to rotation, thus prohibiting the existence of differently oriented instances of the target pattern on the same grid. We propose a modified Isotropic NCA (IsoNCA) model that does not have this limitation. We demonstrate that such cell systems can be trained to grow accurate asymmetrical patterns through either of two methods: (1) by breaking symmetries using structured seeds or (2) by introducing a rotation-reflection invariant training objective and relying on symmetry-breaking caused by asynchronous cell updates.
翻译:通过个体细胞(形态形成)之间的局部互动模拟多细胞有机体建立和保持其身体的能力是发展生物学的长期挑战。最近,提出了神经细胞自动模型(NCA)模式,作为寻找产生理想全球行为的本地系统规则的一种方法,例如通过反复对从单一细胞开始的网格适用相同的规则,从而形成一个预设的目标模式。在这项工作中,我们争辩说,最初的成长中NCA模式有一个重要的局限性:学习更新规则的反向性。这意味着存在一个外部因素,使细胞转向某一特定方向。换句话说,基础系统的“物理”规则并非易变,因此禁止同一电网存在目标模式的不同方向。我们建议采用一个没有这种限制的经修改的Isotopic NCA(IsoNCA)模式。我们证明,这种细胞系统可以通过两种方法来训练如何形成准确的对称模式:(1)用结构的种子打破对称,或者(2)通过采用对目标进行旋转式分析的方式,通过对目标进行硬性分析,对细胞进行自转式分析,从而对目标进行自我调节。