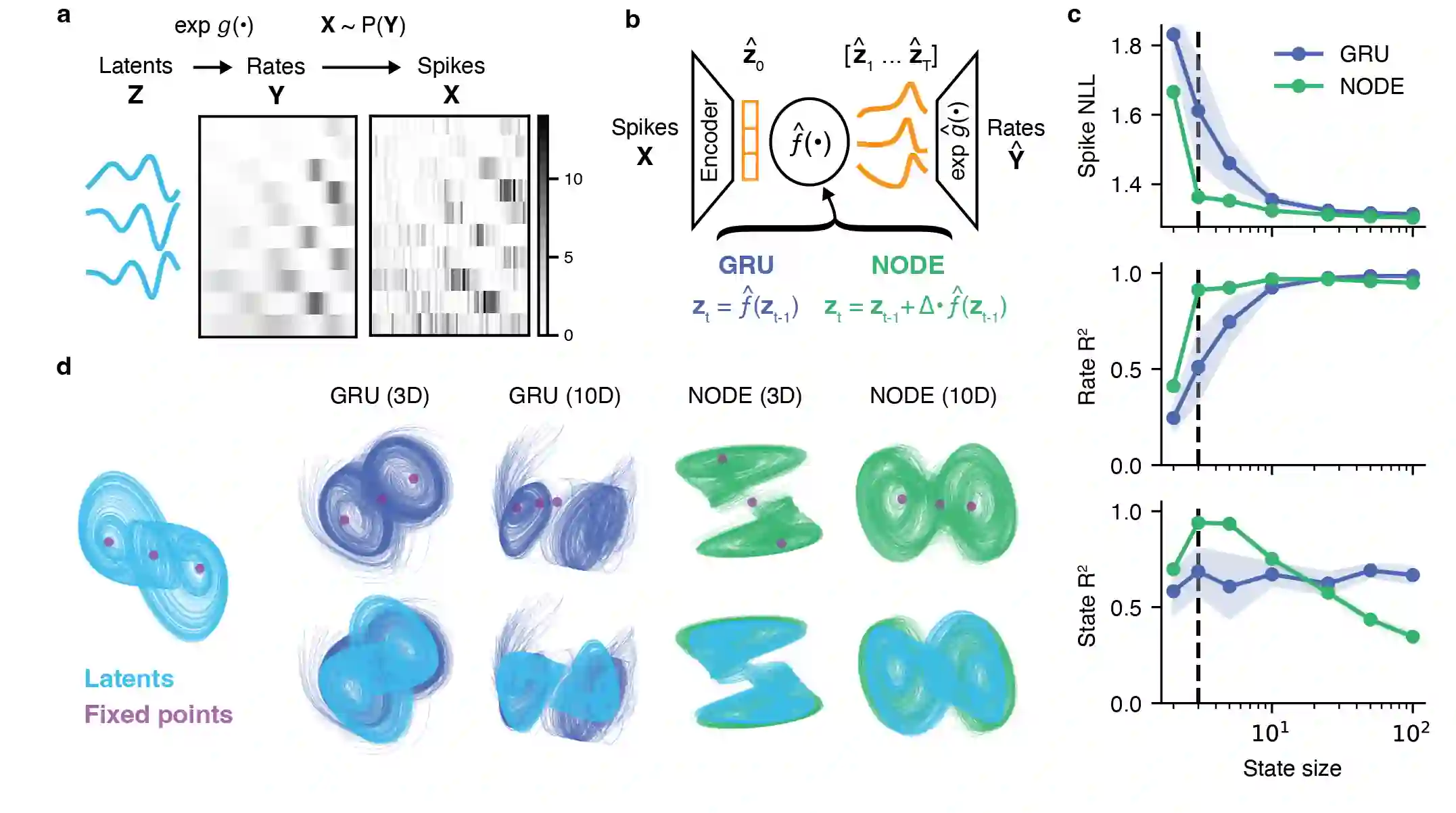
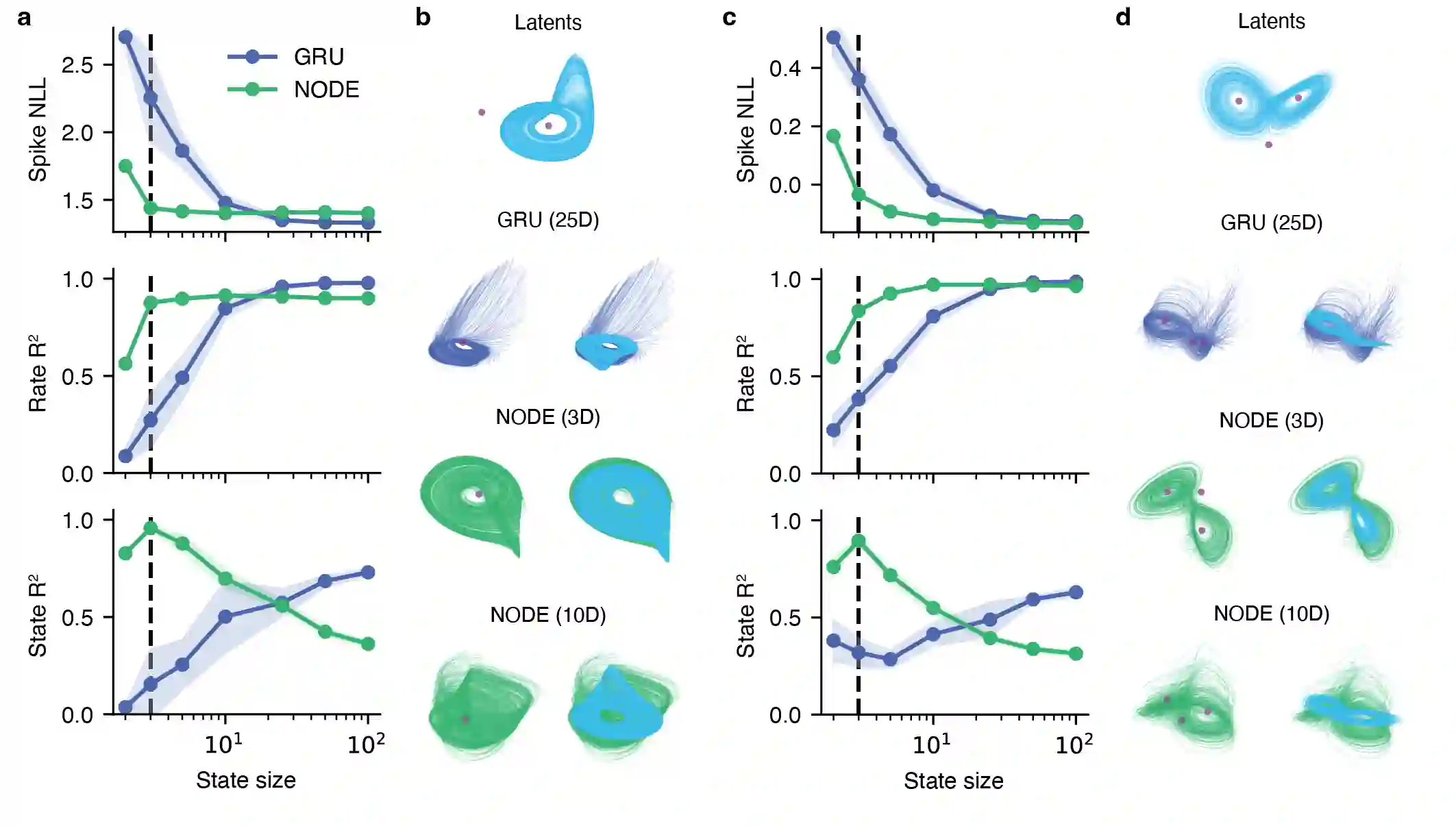
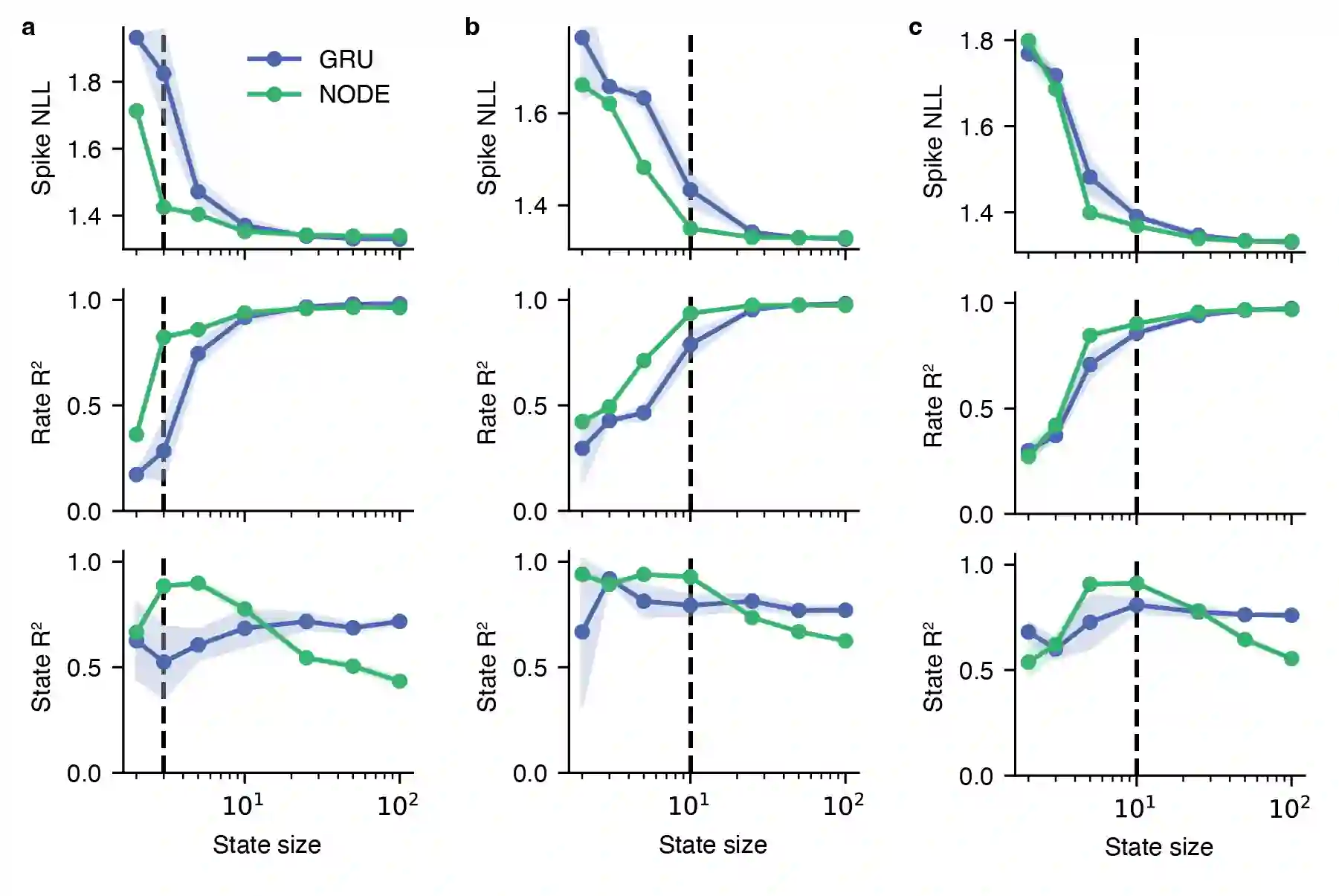
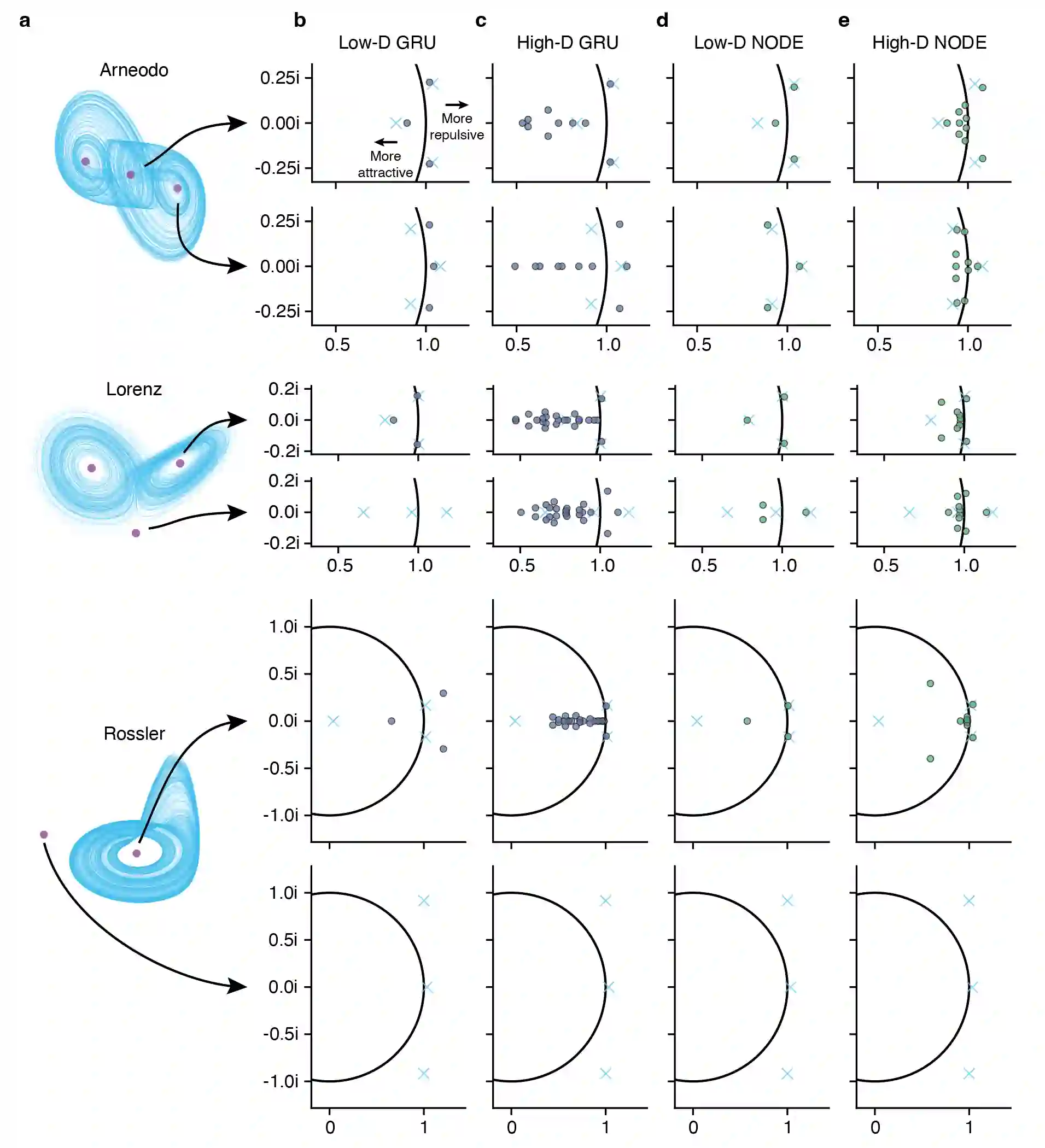
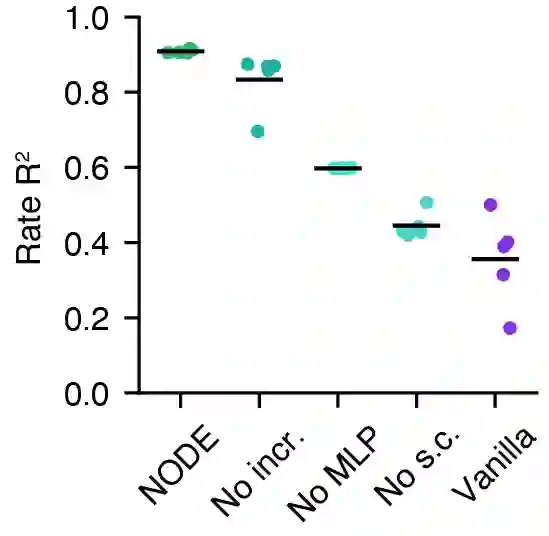
Artificial neural networks that can recover latent dynamics from recorded neural activity may provide a powerful avenue for identifying and interpreting the dynamical motifs underlying biological computation. Given that neural variance alone does not uniquely determine a latent dynamical system, interpretable architectures should prioritize accurate and low-dimensional latent dynamics. In this work, we evaluated the performance of sequential autoencoders (SAEs) in recovering latent chaotic attractors from simulated neural datasets. We found that SAEs with widely-used recurrent neural network (RNN)-based dynamics were unable to infer accurate firing rates at the true latent state dimensionality, and that larger RNNs relied upon dynamical features not present in the data. On the other hand, SAEs with neural ordinary differential equation (NODE)-based dynamics inferred accurate rates at the true latent state dimensionality, while also recovering latent trajectories and fixed point structure. Ablations reveal that this is mainly because NODEs (1) allow use of higher-capacity multi-layer perceptrons (MLPs) to model the vector field and (2) predict the derivative rather than the next state. Decoupling the capacity of the dynamics model from its latent dimensionality enables NODEs to learn the requisite low-D dynamics where RNN cells fail. Additionally, the fact that the NODE predicts derivatives imposes a useful autoregressive prior on the latent states. The suboptimal interpretability of widely-used RNN-based dynamics may motivate substitution for alternative architectures, such as NODE, that enable learning of accurate dynamics in low-dimensional latent spaces.
翻译:暂无翻译