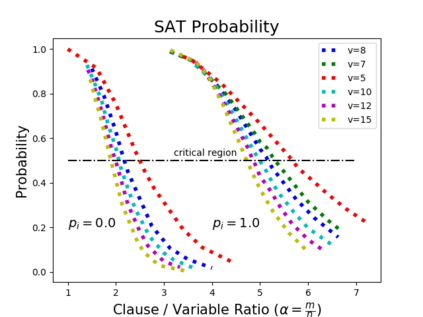
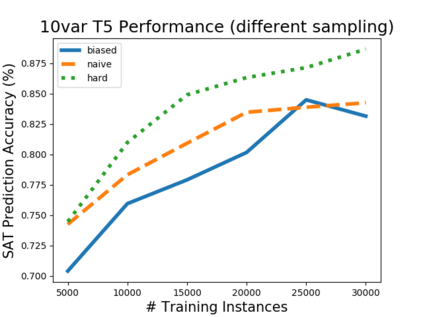
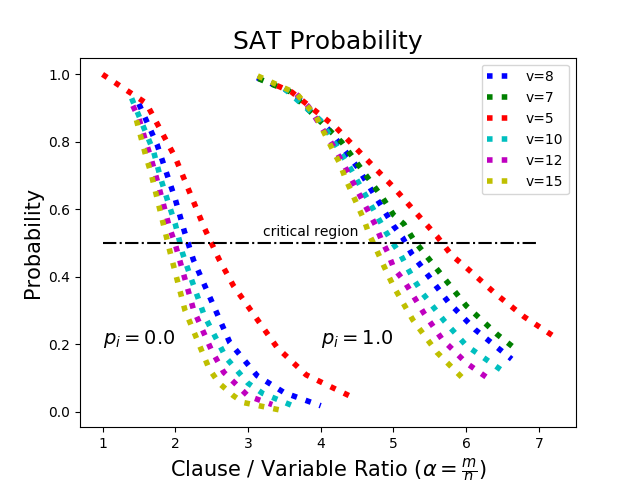
Investigating the reasoning abilities of transformer models, and discovering new challenging tasks for them, has been a topic of much interest. Recent studies have found these models to be surprisingly strong at performing deductive reasoning over formal logical theories expressed in natural language. A shortcoming of these studies, however, is that they do not take into account that logical theories, when sampled uniformly at random, do not necessarily lead to hard instances. We propose a new methodology for creating challenging algorithmic reasoning datasets that focus on natural language satisfiability (NLSat) problems. The key idea is to draw insights from empirical sampling of hard propositional SAT problems and from complexity-theoretic studies of language. This methodology allows us to distinguish easy from hard instances, and to systematically increase the complexity of existing reasoning benchmarks such as RuleTaker. We find that current transformers, given sufficient training data, are surprisingly robust at solving the resulting NLSat problems of substantially increased difficulty. They also exhibit some degree of scale-invariance - the ability to generalize to problems of larger size and scope. Our results, however, reveal important limitations too: a careful sampling of training data is crucial for building models that generalize to larger problems, and transformer models' limited scale-invariance suggests they are far from learning robust deductive reasoning algorithms.
翻译:调查变压器模型的推理能力并发现对变压器模型的新的具有挑战性的任务,这是一个非常令人感兴趣的专题。最近的研究发现,这些模型在对自然语言表达的正式逻辑理论进行推理推理学的实验性推理方面,令人惊讶地表现出很强的强力。然而,这些研究的一个缺点是,它们没有考虑到逻辑理论,当统一随机抽样时,并不一定会导致困难的出现。我们提出了一种新的方法,以创建具有挑战性的算法推理数据集,侧重于自然语言可比较性问题。关键的想法是从硬性理论SAT问题和语言复杂理论研究的实验性抽样中提取洞见。这种方法使我们能够很容易地区分困难的实例,并系统地提高现有推理基准的复杂性,例如规则实验仪。我们发现,由于有足够的培训数据,目前的变压器在解决由此产生的NLSat系统问题方面,难度大得多,令人惊讶。它们也表现出某种程度的偏差,即能够将问题概括到更大的规模和范围。然而,我们的结果也揭示了重要的局限性:仔细地对培训数据进行抽样分析,对于构建更稳健的模型来说,从更精确的推论到更广义的推论,意味着是更大规模的推论问题。