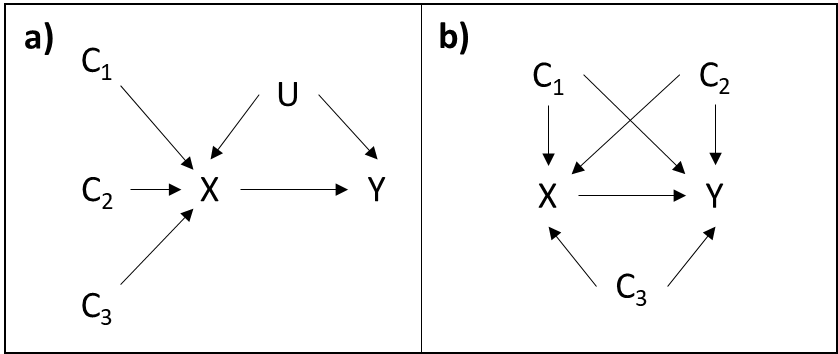
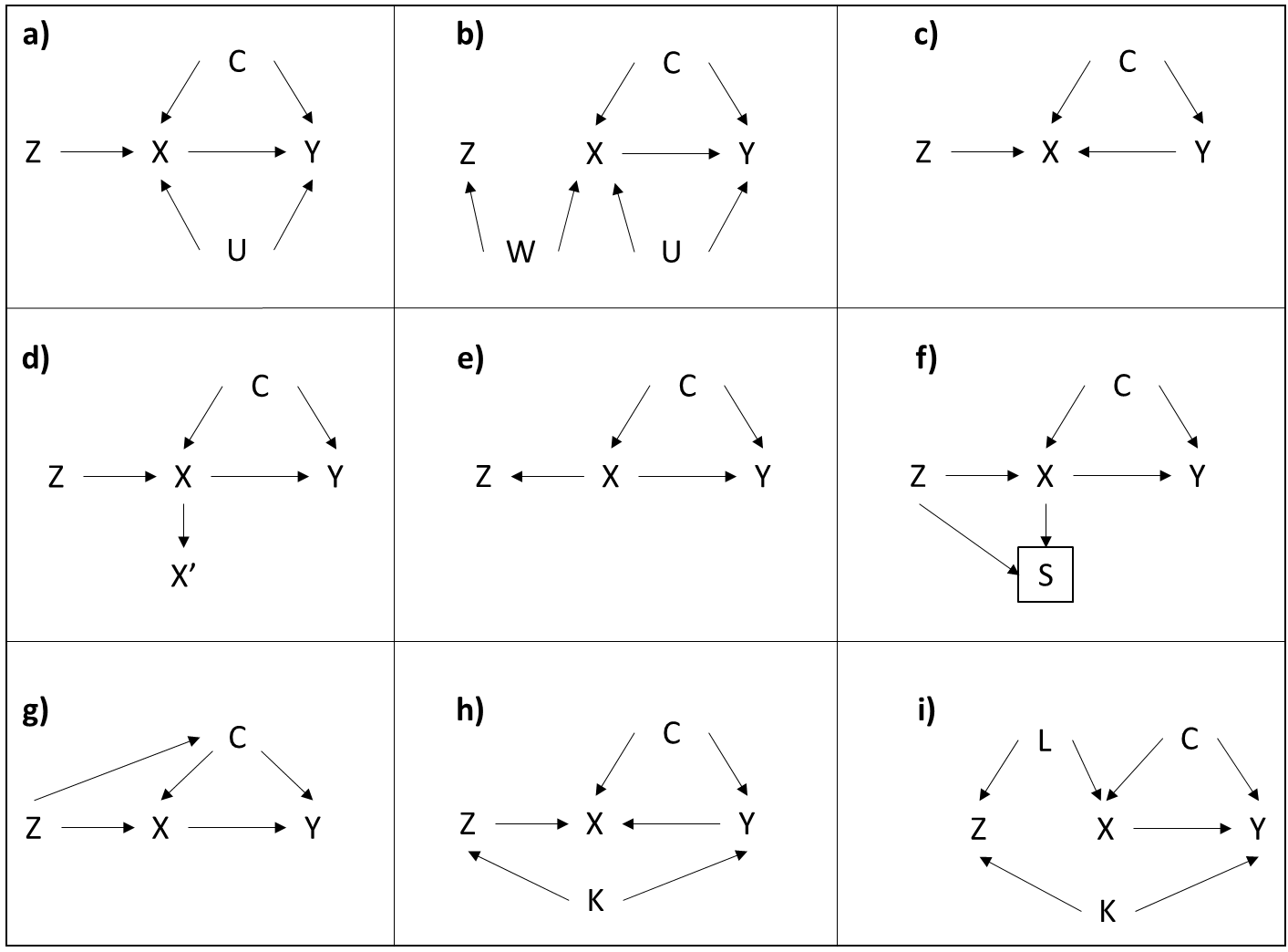
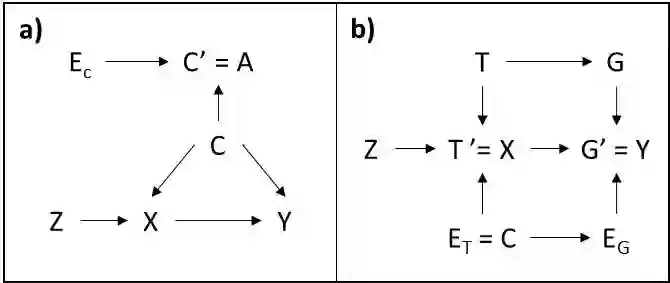
The possibility of unmeasured confounding is one of the main limitations for causal inference from observational studies. There are different methods for partially empirically assessing the plausibility of unconfoundedness. However, most currently available methods require (at least partial) assumptions about the confounding structure, which may be difficult to know in practice. In this paper we describe a simple strategy for empirically assessing the plausibility of conditional unconfoundedness (i.e., whether the candidate set of covariates suffices for confounding adjustment) which does not require any assumptions about the confounding structure, requiring instead assumptions related to temporal ordering between covariates, exposure and outcome (which can be guaranteed by design), measurement error and selection into the study. The proposed method essentially relies on testing the association between a subset of covariates (those associated with the exposure given all other covariates) and the outcome conditional on the remaining covariates and the exposure. We describe the assumptions underlying the method, provide proofs, use simulations to corroborate the theory and illustrate the method with an applied example assessing the causal effect of length-for-age measured in childhood and intelligence quotient measured in adulthood using data from the 1982 Pelotas (Brazil) birth cohort. We also discuss the implications of measurement error and some important limitations.
翻译:暂无翻译