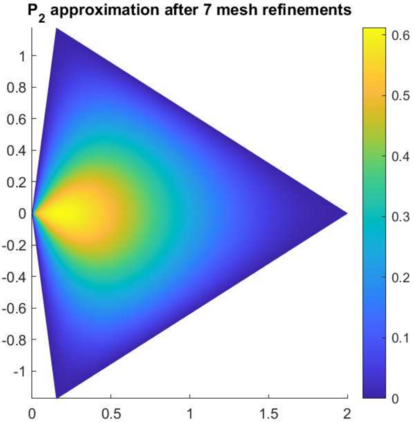
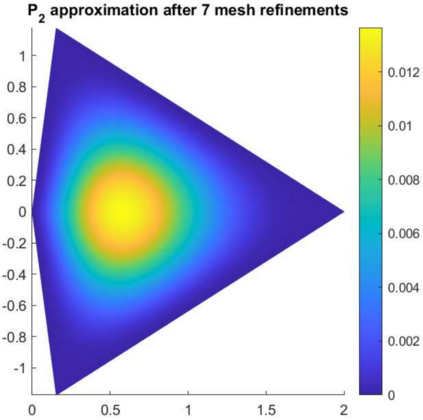
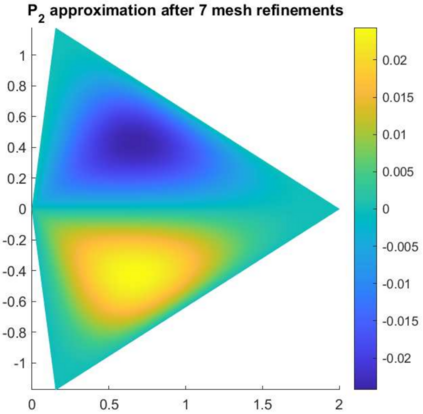
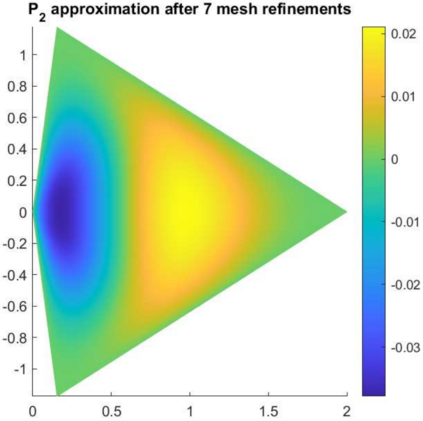
In this paper, we study the biharmonic equation with Dirichlet boundary conditions in a polygonal domain. In particular, we propose a method that effectively decouples the fourth-order problem into a system of two Poison equations and one Stokes equation, or a system of one Stokes equation and one Poisson equation. It is shown that the solution of each system is equivalent to that of the original fourth-order problem on both convex and non-convex polygonal domains. Two finite element algorithms are in turn proposed to solve the decoupled systems. In addition, we show the regularity of the solutions in each decoupled system in both the Sobolev space and the weighted Sobolev space, and we derive the optimal error estimates for the numerical solutions on both quasi-uniform meshes and graded meshes. Numerical test results are presented to justify the theoretical findings.
翻译:在本文中,我们研究了多边形域中Drichlet边界条件的双调方程。 特别是, 我们提出了一种方法, 将第四级问题有效地分解为两个毒性方程式和一个斯托克斯方程式的系统, 或一个斯托克斯方程式和一个Poisson方程式的系统。 这表明每个系统的解决方案都相当于 convex 和非convex 多边形域的最初第四级问题。 两种有限的元素算法又被提出来解决分解的系统。 此外, 我们展示了索博列夫空间和加权索博列夫空间中每个拆解系统中的解决方案的规律性, 并且我们得出了半统一的中间体和分级的中间体数字解决方案的最佳误差估计值。 数字测试结果被提出来证明理论结论的合理性。