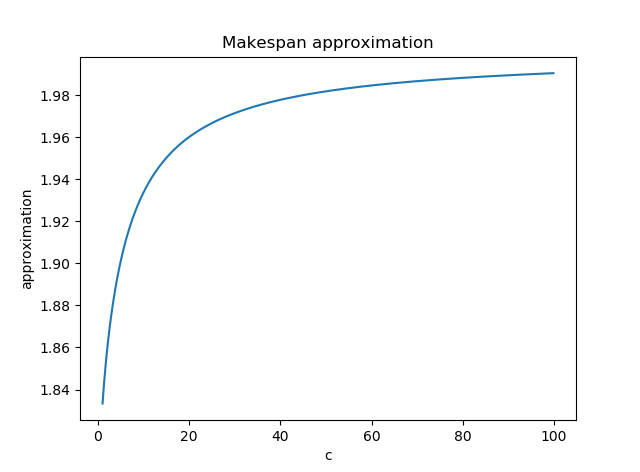
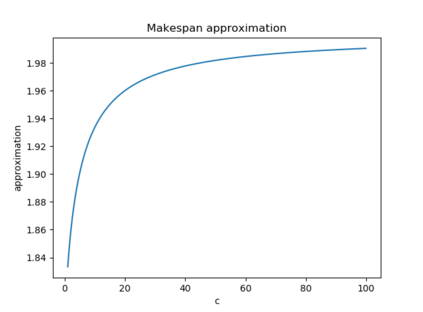
Motivated by the classic Generalized Assignment Problem, we consider the Graph Balancing problem in the presence of orientation costs: given an undirected multi-graph G = (V,E) equipped with edge weights and orientation costs on the edges, the goal is to find an orientation of the edges that minimizes both the maximum weight of edges oriented toward any vertex (makespan) and total orientation cost. We present a general framework for minimizing makespan in the presence of costs that allows us to: (1) achieve bicriteria approximations for the Graph Balancing problem that capture known previous results (Shmoys-Tardos [Math. Progrm. 93], Ebenlendr-Krc\'al- Sgall [Algorithmica 14], and Wang-Sitters [Inf. Process. Lett. 16]); and (2) achieve bicriteria approximations for extensions of the Graph Balancing problem that admit hyperedges and unrelated weights. Our framework is based on a remarkably simple rounding of a strengthened linear relaxation. We complement the above by presenting bicriteria lower bounds with respect to the linear programming relaxations we use that show that a loss in the total orientation cost is required if one aims for an approximation better than 2 in the makespan.
翻译:以典型的通用任务问题为动力,我们考虑了在定向成本面前的平衡问题:鉴于在边缘上装有边缘重量和定向成本的未定向多光学G = (V,E) = (V,E) 的多光学G = (V,E) = (V,E) 的边缘,目标是找到一个边缘方向,将面向任何顶点(Makespan)的边缘的最大重量和总方向成本降低到最低程度;我们提出了一个在成本上最大限度地减少平衡问题的总体框架,使我们能够:(1) 达到双标准近似于平衡问题的双向近似值,从而捕捉到已知的先前结果(Shmoys-Tardos [Matth.Progrm. 93], Ebenlendr-Krc\'al-Sgarll [Algorithmica 14] 和Wang-Sritters [Inf. procroc.Lett. 16] ;以及(2) 实现双标准近似近似值的扩展线性近似度,如果在2项目标上提出比线性调整更符合要求的成本的话,则更接近,则更接近于线性地展示成本。