Tilting the playing field: Dynamical loss functions for machine learning

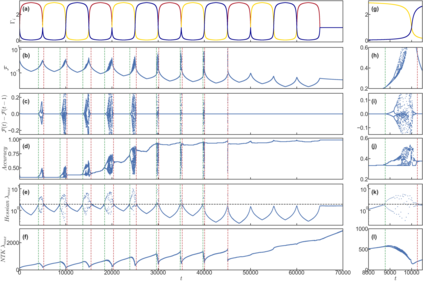
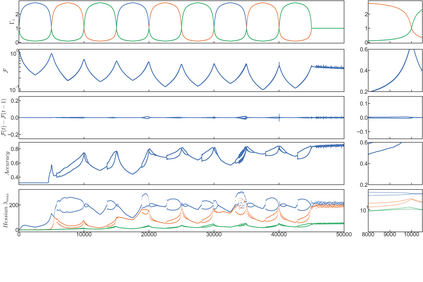
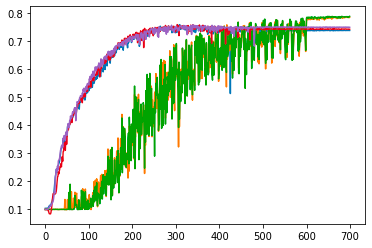
We show that learning can be improved by using loss functions that evolve cyclically during training to emphasize one class at a time. In underparameterized networks, such dynamical loss functions can lead to successful training for networks that fail to find a deep minima of the standard cross-entropy loss. In overparameterized networks, dynamical loss functions can lead to better generalization. Improvement arises from the interplay of the changing loss landscape with the dynamics of the system as it evolves to minimize the loss. In particular, as the loss function oscillates, instabilities develop in the form of bifurcation cascades, which we study using the Hessian and Neural Tangent Kernel. Valleys in the landscape widen and deepen, and then narrow and rise as the loss landscape changes during a cycle. As the landscape narrows, the learning rate becomes too large and the network becomes unstable and bounces around the valley. This process ultimately pushes the system into deeper and wider regions of the loss landscape and is characterized by decreasing eigenvalues of the Hessian. This results in better regularized models with improved generalization performance.