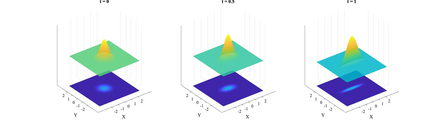
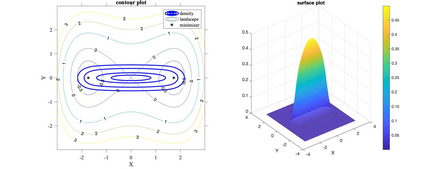
We initiate the study of quantum algorithms for escaping from saddle points with provable guarantee. Given a function $f\colon\mathbb{R}^{n}\to\mathbb{R}$, our quantum algorithm outputs an $\epsilon$-approximate second-order stationary point using $\tilde{O}(\log^{2} n/\epsilon^{1.75})$ queries to the quantum evaluation oracle (i.e., the zeroth-order oracle). Compared to the classical state-of-the-art algorithm by Jin et al. with $\tilde{O}(\log^{6} n/\epsilon^{1.75})$ queries to the gradient oracle (i.e., the first-order oracle), our quantum algorithm is polynomially better in terms of $n$ and matches its complexity in terms of $1/\epsilon$. Our quantum algorithm is built upon two techniques: First, we replace the classical perturbations in gradient descent methods by simulating quantum wave equations, which constitutes the polynomial speedup in $n$ for escaping from saddle points. Second, we show how to use a quantum gradient computation algorithm due to Jordan to replace the classical gradient queries by quantum evaluation queries with the same complexity. Finally, we also perform numerical experiments that support our quantum speedup.
翻译:我们开始研究量子算法, 以便以可变保证来逃离马鞍点。 根据一个函数 $f\ cron\ mathb{R ⁇ n ⁇ to\mathb{R}$, 我们的量子算法输出了一个 $\ epsilon$- 近二阶固定点, 使用$\ tilde{O} (log ⁇ 2} n/\\\\ epsilon} n1. 75}, 我们的量子算法在质子评估或质子( e., e., 零顺序) 的质子算法查询。 与金等人的典型最新水平算法相比, 我们用 $\ talde{O} (log_6} n/\ e/\ epsilon}\ 1. 75} 我们的量子运算算算算算法, 以1/\ eqolon=clegal 递增量级算法, 我们的量级级算算算法, 以最终的量级级算算法, 以美元取代了我们的量级级级算。