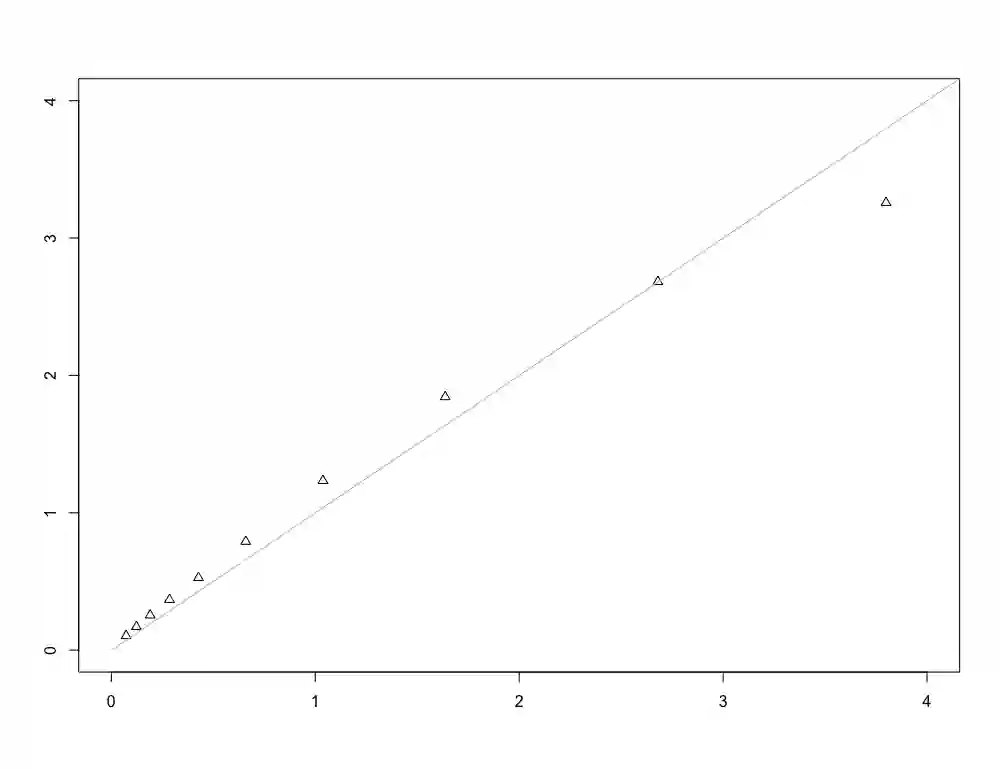
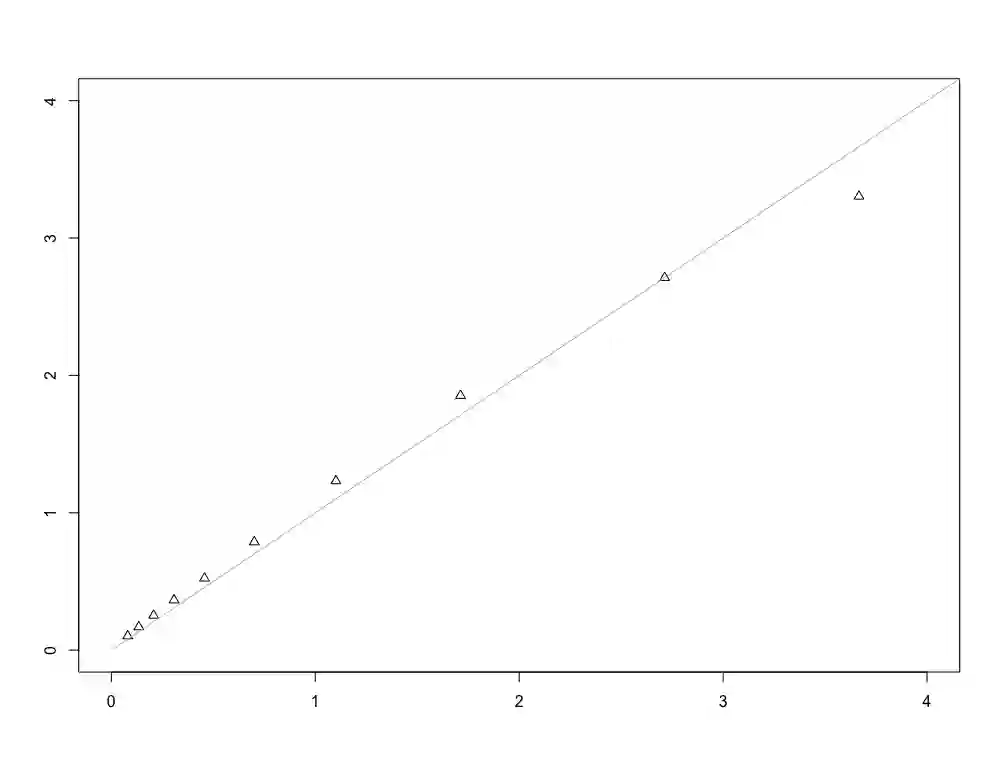
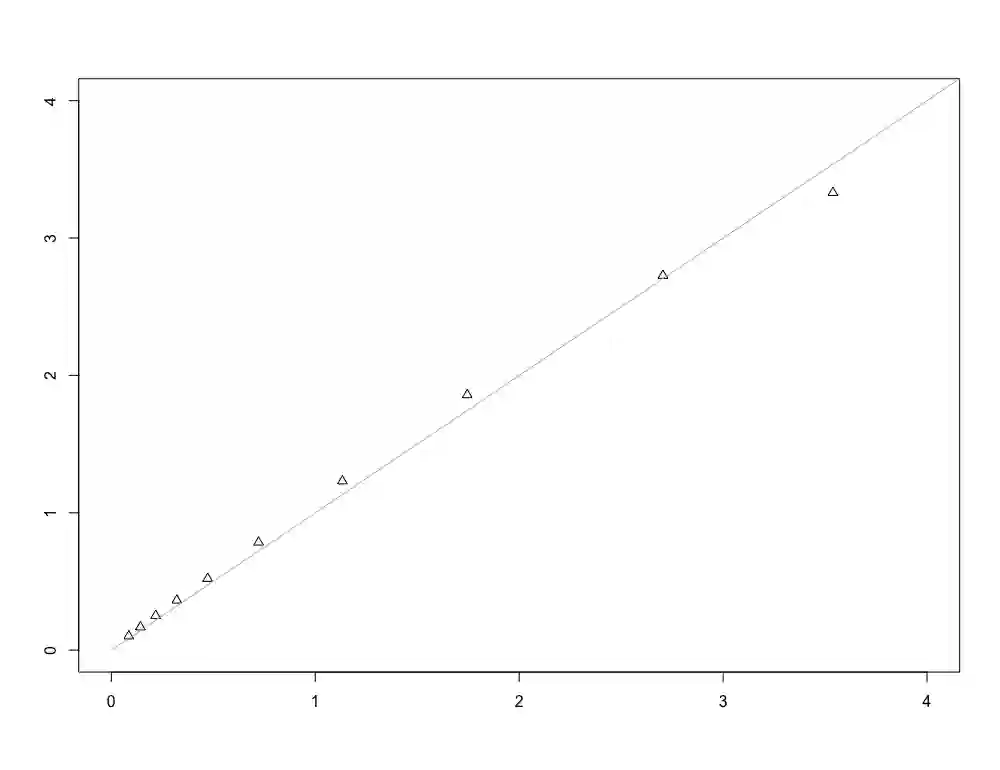
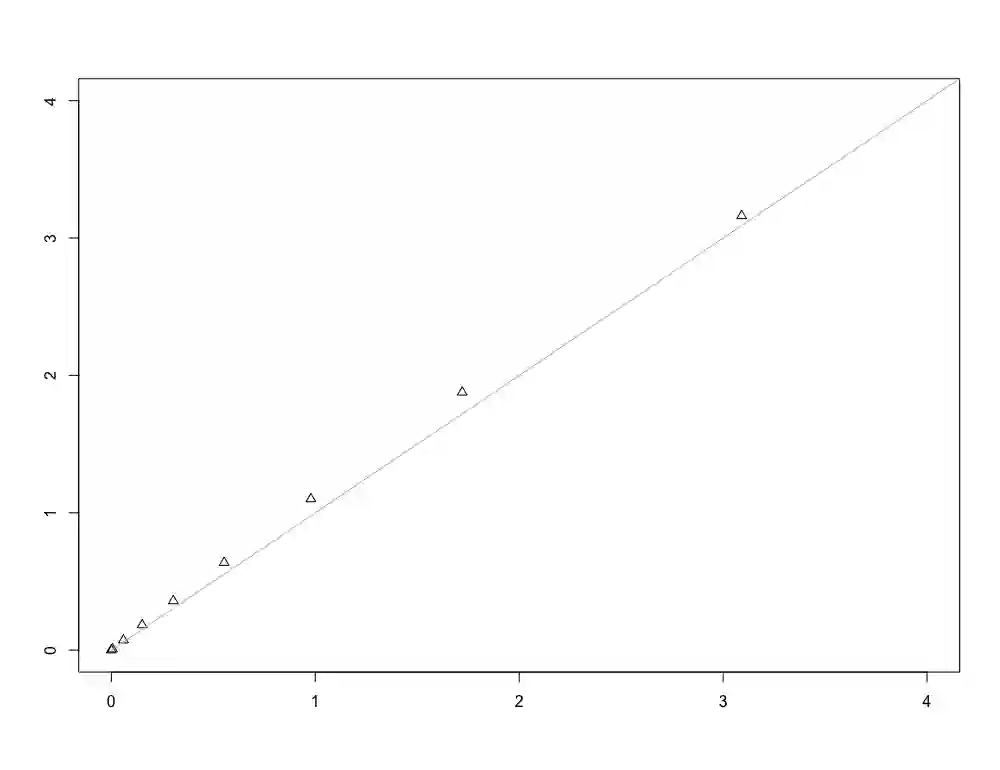
In this paper, we consider the empirical spectral distribution of the sample correlation matrix and investigate its asymptotic behavior under mild assumptions on the data's distribution, when dimension and sample size increase at the same rate. First, we give a characterization for the limiting spectral distribution to follow a Marchenko-Pastur law assuming that the underlying data matrix consists of i.i.d. entries. Subsequently, we provide the limiting spectral distribution of the sample correlation matrix when allowing for a dependence structure within the columns of the data matrix. In contrast to previous works, the fourth moment of the data may be infinite, resulting in a fundamental structural difference. More precisely, the standard argument of approximating the sample correlation matrix by its sample covariance companion breaks down and novel techniques for tackling the challenging dependency structure of the sample correlation matrix are introduced.
翻译:在本文中,我们考虑抽样相关矩阵的经验光谱分布,并根据对数据分布的轻度假设调查其无症状行为,当尺寸和样本规模以同样速度增加时。首先,我们按照马肯科-帕斯图尔法对限制光谱分布进行定性,假设基本数据矩阵包括一.d.条目。随后,我们提供样本相关矩阵的有限光谱分布,以允许数据矩阵各栏内依赖结构。与以往的工程不同,数据第四刻可能无穷无尽,造成根本性的结构差异。更确切地说,我们提出标准的论点,即通过样本共变式伴体对样本相关矩阵进行近似比对样本相关矩阵进行对比,并采用新的技术处理样本相关矩阵具有挑战性的依赖结构。