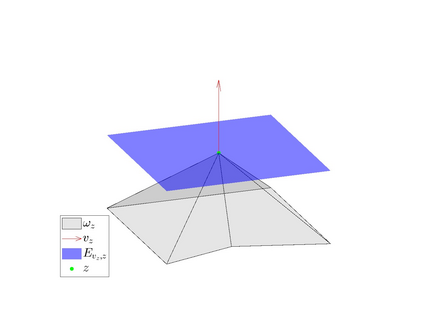
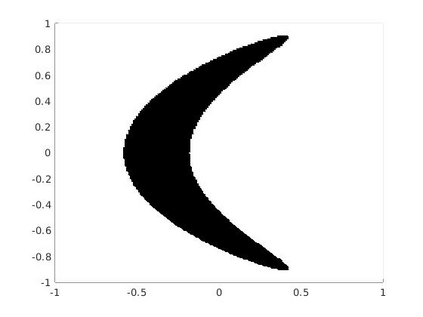
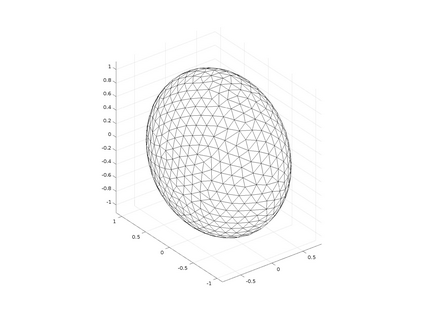
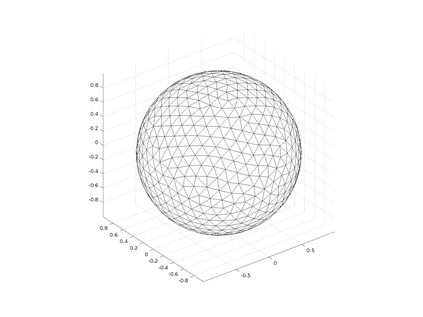
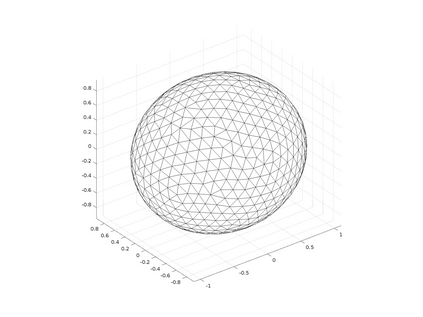
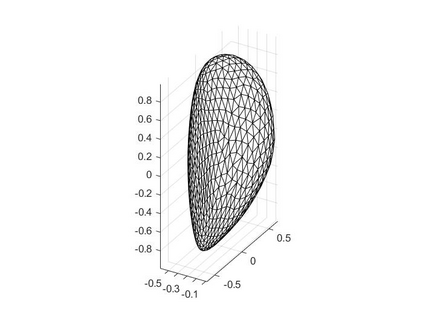
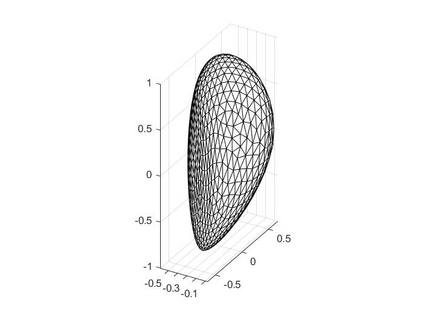
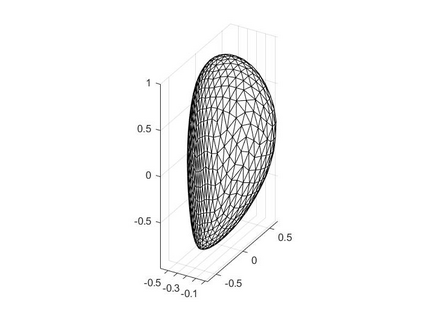
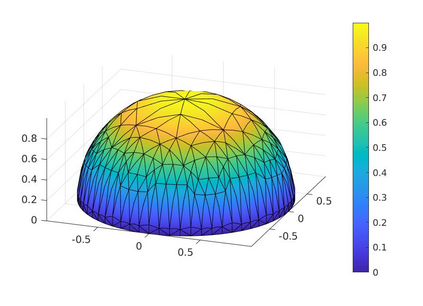
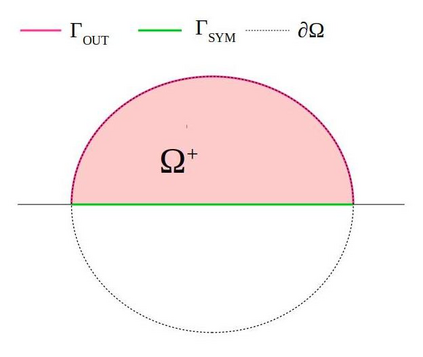
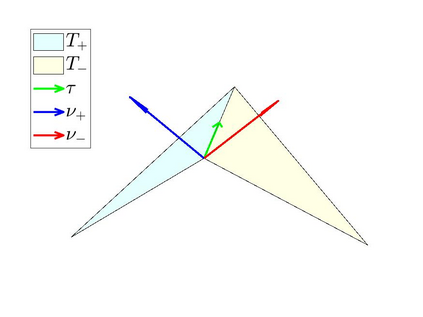
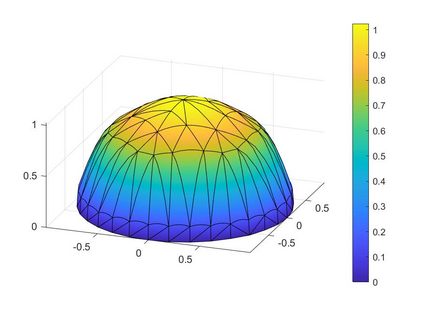
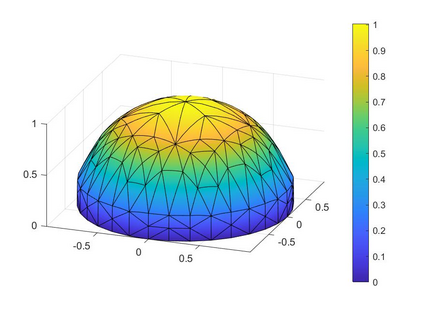
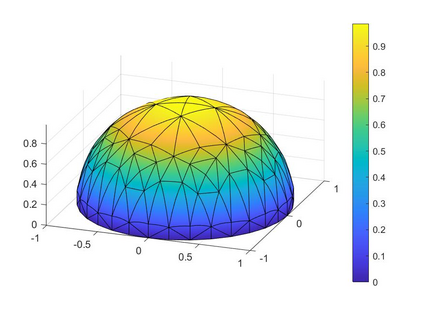
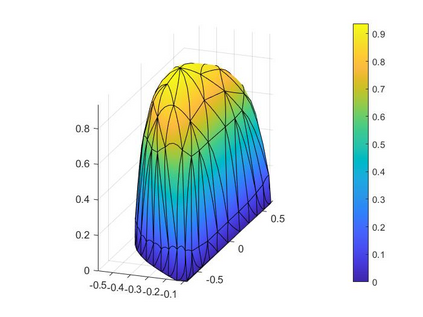
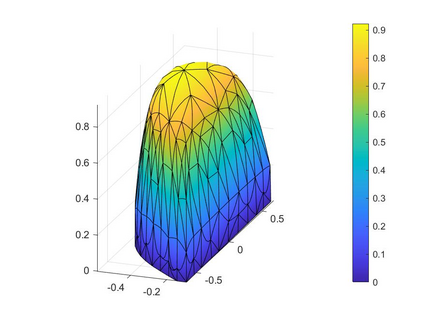
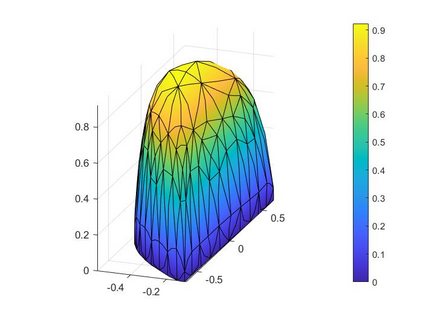
In the optimization of convex domains under a PDE constraint numerical difficulties arise in the approximation of convex domains in $\mathbb{R}^3$. Previous research used a restriction to rotationally symmetric domains to reduce shape optimization problems to a two-dimensional setting. In the current research, two approaches for the approximation in $\mathbb{R}^3$ are considered. First, a notion of discrete convexity allows for a nearly convex approximation with polyhedral domains. An alternative approach is based on the recent observation that higher order finite elements can approximate convex functions conformally. As a second approach these results are used to approximate optimal convex domains with isoparametric convex domains. The proposed algorithms were tested on shape optimization problems constrained by a Poisson equation and both algorithms achieved similar results.
翻译:暂无翻译