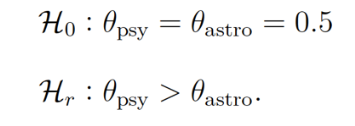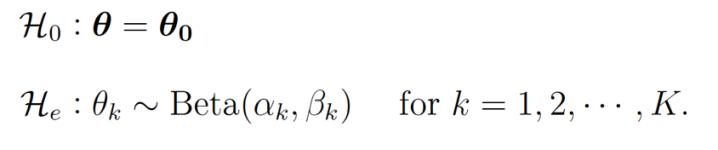Current developments in the statistics community suggest that modern statistics education should be structured holistically, that is, by allowing students to work with real data and to answer concrete statistical questions, but also by educating them about alternative frameworks, such as Bayesian inference. In this article, we describe how we incorporated such a holistic structure in a Bayesian research project on ordered binomial probabilities. The project was conducted with a group of three undergraduate psychology students who had basic knowledge of Bayesian statistics and programming, but lacked formal mathematical training. The research project aimed to (1) convey the basic mathematical concepts of Bayesian inference; (2) have students experience the entire empirical cycle including collection, analysis, and interpretation of data and (3) teach students open science practices.
翻译:统计界目前的发展情况表明,现代统计教育的结构应该整体化,即允许学生使用真实数据,回答具体的统计问题,但也让他们了解替代框架,如贝耶斯推断。我们在本篇文章中描述了我们如何将这种整体结构纳入巴伊斯研究的有顺序的二元概率项目。该项目是与三名本科心理学学生一起进行的,他们基本了解巴耶斯统计和方案编制,但缺乏正式的数学培训。研究项目旨在(1) 传达巴耶斯推论的基本数学概念;(2) 使学生体验整个经验周期,包括数据的收集、分析和解释,(3) 教育学生开放科学实践。