游戏 |《数学女孩》:在青春故事中走近数学

在动人的故事中走近数学
在青春的浪漫中理解数学
《数学女孩》系列是日本知名技术作家结城浩的数学科普作品。不同于一般的数学科普书,《数学女孩》以青春小说的方式讲解数学难题,形式新颖,引人入胜,吸引了一大批热爱数学的粉丝。也有很多读者表示,这套书使他们重新燃起对数学的兴趣。
主人公“我”是一名高中男生,喜爱数学,兴趣是讨论计算公式,经常独自在书桌前思考数学问题。进入高中后,先后结识了擅长数学、聪明机敏的天才少女米尔嘉,好奇心旺盛、活力十足又努力认真的学妹泰朵拉,以及沉默寡言的计算机高手理纱,再加上头脑灵活,在“我”的带动下逐渐喜欢上数学的表妹尤里,几个年轻人一起在数学的世界中畅游,发现数学之美!

[遇见] 根据《数学女孩4:随机算法》前 2 章制作了一个 AVG 游戏短篇. 小编也是边做边学制作, 各位大触轻拍. 游戏在线运行即可, 链接请见文末或扫描上面二维码.
如果对制作类似 AVG 游戏感兴趣, 欢迎加入即将建立的 [遇见数游社团], 不论想找分享精彩剧本, 寻找制作合作伙伴、或是分享游戏创作心得, 都欢迎加入社团哦!

下面节选书中及游戏部分内容分享给大家:
哈哈
第1个個故事
The first tory
白
1
绝不会输的赌博

“我们来比赛吧,哥哥!”尤里叫我。
“好啊,今天比什么?”我回应道。
“我来出题,咱们认真地决一胜负吧!”

“呃 …… 因为对称性(对称性是说爱丽丝和鲍勃在比赛中的地位相同,谁也不比谁占优势,所以获胜的概率相同。但此处主人公大意遗漏了平局的情况,因此得出了错误的结论。——译者注),爱丽丝获胜的概率不就是 嘛。”我回答说。

“啊,不对。两个人——”
“你漏掉了两个人平局的情况。”尤里接过我的话。
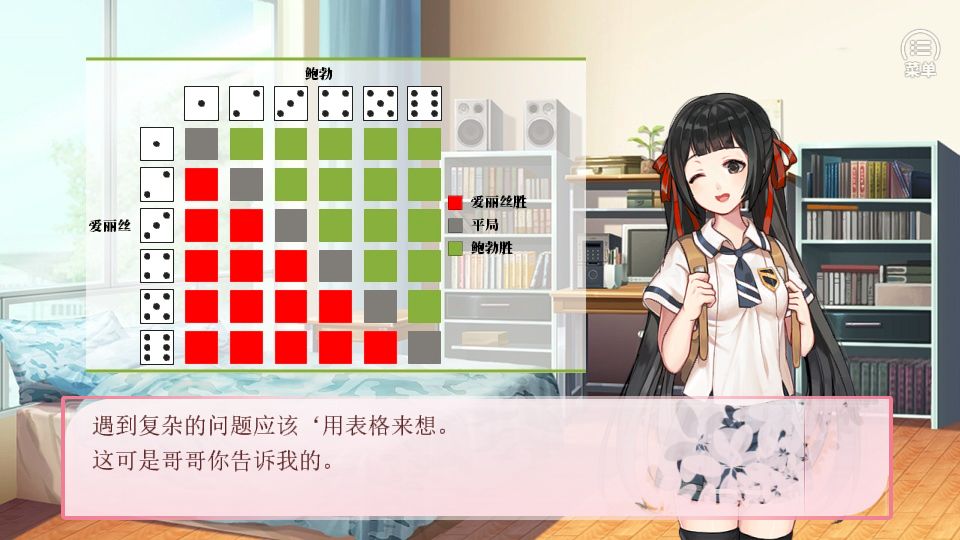
“是我大意了。”我说道,“爱丽丝的骰子的点数有 6 种,与之相对应,鲍勃的骰子的点数也有 6 种。也就是说总共有 6 × 6 = 36 种情况。这 36 种情况中每一种情况发生的概率都相同。”
所有情况数 = 爱丽丝的 6 种 × 鲍勃的 6 种= 36 种
我看着点头的尤里,继续解释。
“36 种情况中,爱丽丝和鲍勃的点数相等的情况有 6 种,此时结果为平局。所以能分出胜负的情况就是 36 − 6 = 30 种。

“嗯嗯。”
“所以,爱丽丝获胜的概率就是这样的。”我接着说。
“这次答对啦。爱丽丝获胜的概率是 。哥哥,你漏掉了两个人平局的情况,没想到哥哥也会犯这种低级错误喵~”尤里用猫语说道。
“我也会有失手的时候呀。”
“遇到复杂的问题应该‘用表格来想’,这可是哥哥你告诉我的。”
……
……
……
<< 滑动查看游戏截图 >>
游戏截图(共4张)
more+
上文节选自《数学女孩 4: 随机算法》, 已获出版社授权许可, [遇见数学] 特此表示感谢! 游戏截图自橙光游戏, 更多内容还请见游戏或书籍吧.
☟ 点击【阅读原文】玩一下《数学女孩 4》的游戏?