为什么K-FAC这种二阶优化方法没有得到广泛的应用？

2019 年 9 月 21 日 极市平台

加入极市专业CV交流群，与6000+来自腾讯，华为，百度，北大，清华，中科院等名企名校视觉开发者互动交流！更有机会与李开复老师等大牛群内互动！

同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总，行业技术交流。关注 极市平台 公众号，回复 加群，立刻申请入群~

本文选自知乎问答，仅用于学术交流，侵删。

为什么K-FAC这种二阶优化方法没有得到广泛的应用？

https://www.zhihu.com/question/305694880

知乎高质量回答

1.作者：李振华

https://www.zhihu.com/question/57532048/answer/153255177

一个优化算法如果没有得到广泛的应用，最大的可能就是这方法效果不太行。

K-FAC是一种针对神经网络的层叠结构的近似自然梯度算法。从想法层面上，K-FAC几乎是一种理想的适合于神经网络的优化算法，即充分利用了神经网络本身层叠结构的特点来近似Fisher矩阵。这样的算法直到近些年才发展出来反而令人惊讶。

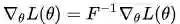
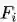
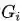
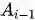
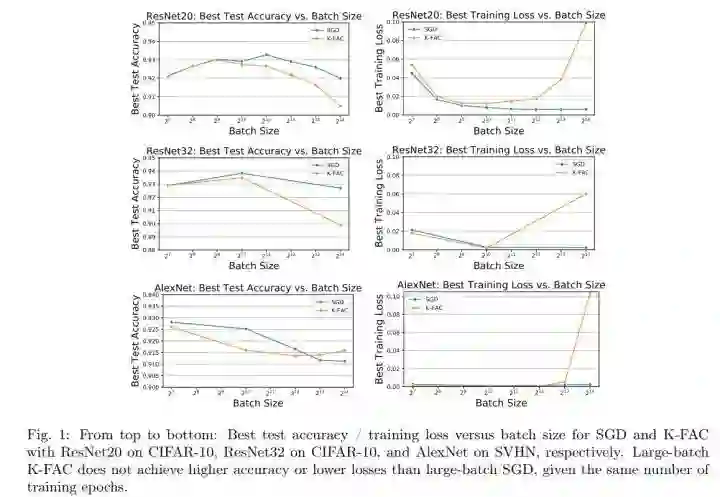
自然梯度定义为：，其中F是分布之间的Fisher Information Matrix。由于神经网络权重数量较大，存储一个完整的F 和计算F的逆会很耗时，这是NG应用到高维问题的一个难点。对于神经网络的分层结构，K-FAC通过神经网络层之间的独立性假设近似，F可以写成一个分块对角结构的矩阵，其第i个块为

其中是第i层对应的 Fisher matrix, 是反向传回来的loss对本层非线性映射之前的输出的梯度，是上一层非线性之后的输出，是Kronecker积. K-FAC通过分块对角的近似F来避免大规模矩阵的存储和矩阵逆的计算。类似二阶算法，K-FAC声称的优势是loss对于运行时间比SGD下降更快。

然而，更多的关于最终accuracy的实验结果是negative的。年初有一篇文章仔细对比了K-FAC和SGD的实验结果，Inefficiency of K-FAC for Large Batch Size Training（链接：https://arxiv.org/abs/1903.06237），其主要的实验观察为：

1、Performance. Even with extensive hyperparameter tuning, K-FAC has comparable, but not superior, train/test performance to SGD (Fig. 1).

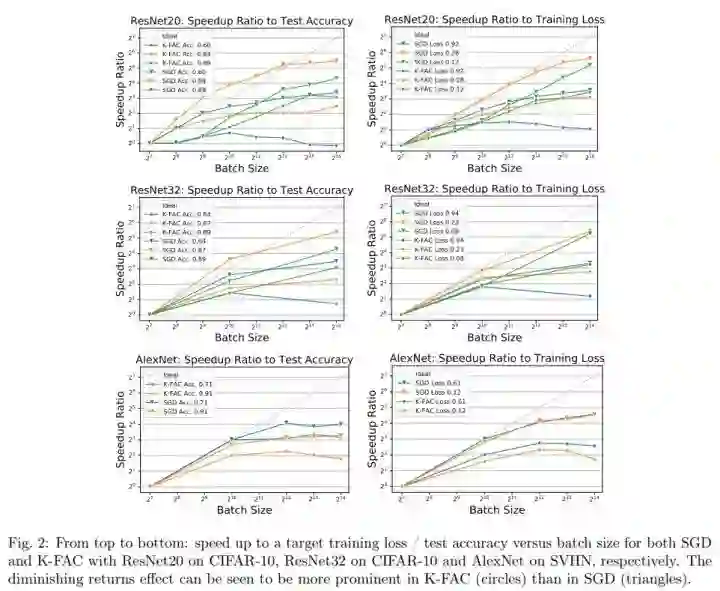
2、Speedup. Both K-FAC and SGD have diminishing returns with the increase of batch size. Increasing batch size for K-FAC yields lower, i.e., less prominent, speedup, as compared with SGD, when measured in terms of iterations (Fig. 2).

3、Hyperparameter Sensitivity. K-FAC hyperparameter sensitivity depends on both batch size and epochs/iterations. For fixed epochs, i.e., running the same number of epochs, larger batch sizes result in greater hyperparameter sensitivity and smaller regions of hyperparameter space which result in “good convergence.” For fixed iterations, i.e., running the same number of iterations, larger batch sizes result in less sensitivity and larger regions of hyperparameter space which result in “good convergence” (Fig. 3, Fig. 4).

二阶方法在确定性问题上通常有收敛速率方面的优势，但是在深度学习问题上的应用总体来说都不太成功，一个可能的原因就是由于梯度本身是通过随机近似估计而来的，使用这个noisy的梯度去近似曲率信息（Hessian 或者 Fisher）都会造成noise的积累和沉淀，高阶信息对noise更敏感，使得Hessian或Fisher很难估计准确。为了提高估计的准确性，增大batch size是一种思路，但是目前结果来看直接增大batch size的有效性很可疑。这不是K-FAC的问题，是自然梯度本就有这样的问题，而K-FAC无法解决这个难点。

目前来说，各种二阶近似方法在DL上都很难战胜SGD，反倒是只保留对角元（如Adam某种程度上可以看成近似Fisher矩阵矩阵的对角元）或者只保留单独的一个方向（类似rank-one 近似的Fisher），对noise的容忍度更高些。

2.作者：信息门下走狗

https://www.zhihu.com/question/305694880/answer/805288399

采用natural gradient的优势可能不是在收敛速度上，也不一定在泛化能力上，毕竟如前面答主所说，统计估计的噪声还是很大的，在实用的意义上，这个二阶信息的优势能否体现出来是很难保证的，恐怕初始值的选择的影响都比这个要大。但是，我觉得从概念上，这个思想是重要的，因为这相当于引入了一个约束，而这个约束的引入对于理解网络的特性非常关键，因为 Fisher metric引入了度量和几何结构，这个度量本身就是为度量随机分布空间的距离量身定造的，而分布是和信息紧密联系的，所以这个东西体现了网络作为信息表述系统的核心特征。

-End-

*延伸阅读

添加极市小助手微信（ID : cv-mart），备注：研究方向-姓名-学校/公司-城市（如：目标检测-小极-北大-深圳），即可申请加入目标检测、目标跟踪、人脸、工业检测、医学影像、三维&SLAM、图像分割等极市技术交流群，更有每月大咖直播分享、真实项目需求对接、干货资讯汇总，行业技术交流，一起来让思想之光照的更远吧~