读懂基础机器学习算法

2017 年 5 月 22 日 产业智能官

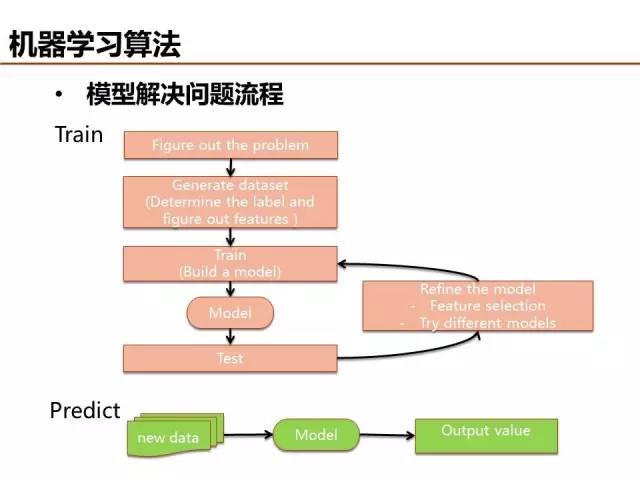
哲学要回答的基本问题是从哪里来、我是谁、到哪里去，寻找答案的过程或许可以借鉴机器学习的套路：组织数据->挖掘知识->预测未来。组织数据即为设计特征，生成满足特定格式要求的样本，挖掘知识即建模，而预测未来就是对模型的应用。

特征设计依赖于对业务场景的理解，可分为连续特征、离散特征和组合高阶特征。本篇重点是机器学习算法的介绍，可以分为监督学习和无监督学习两大类。

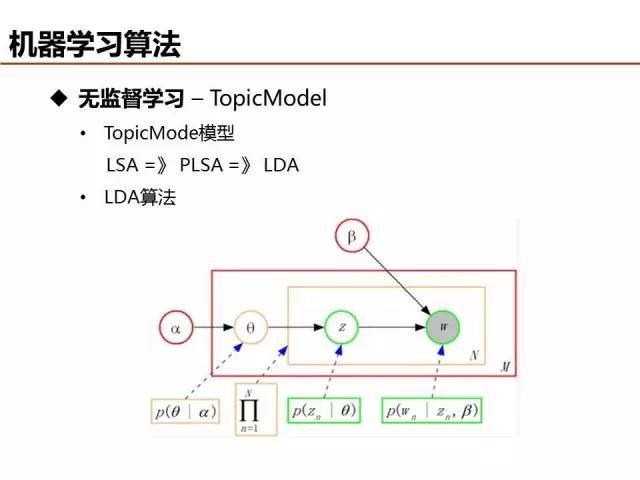
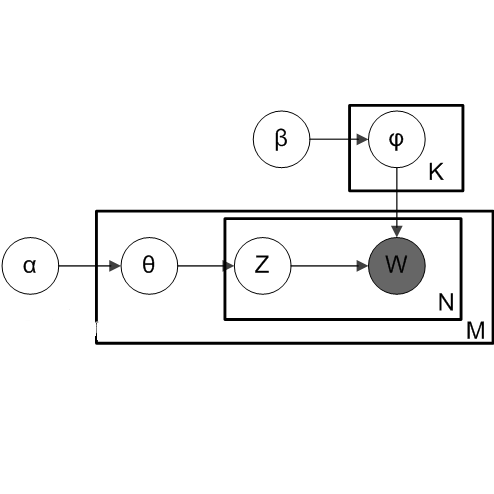
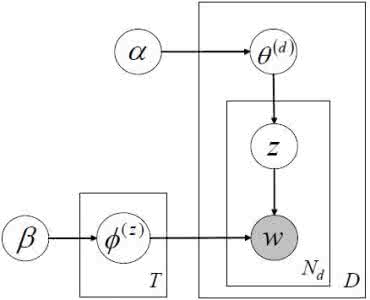
无监督学习算法很多，最近几年业界比较关注主题模型，LSA->PLSA->LDA 为主题模型三个发展阶段的典型算法，它们主要是建模假设条件上存在差异。LSA假设文档只有一个主题，PLSA 假设各个主题的概率分布不变（theta 都是固定的），LDA 假设每个文档和词的主题概率是可变的。

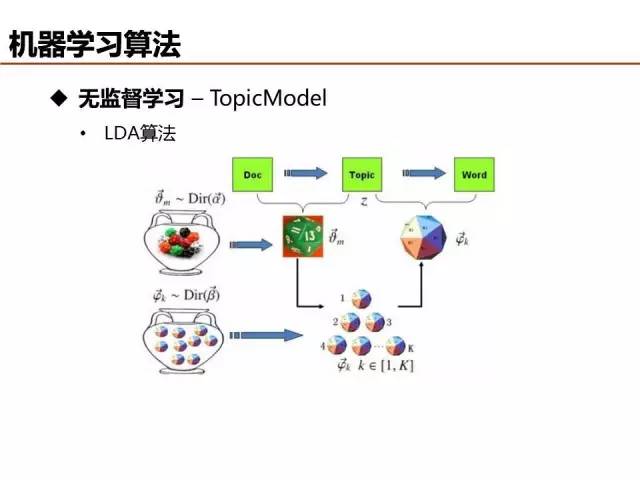
LDA 算法本质可以借助上帝掷骰子帮助理解，详细内容可参加 Rickjin 写的《 LDA 数据八卦》文章，浅显易懂，顺便也科普了很多数学知识，非常推荐。

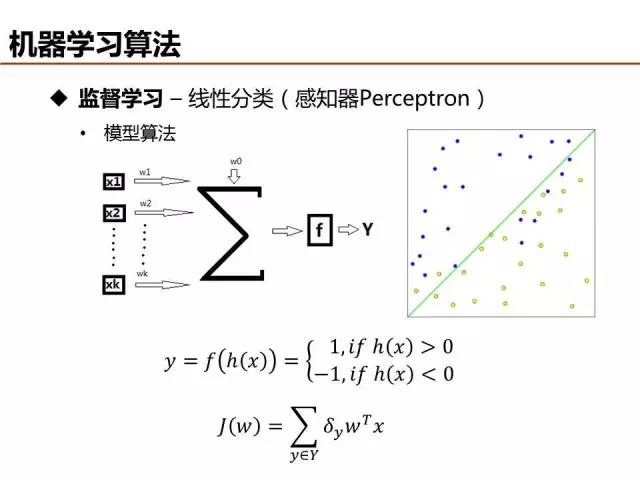
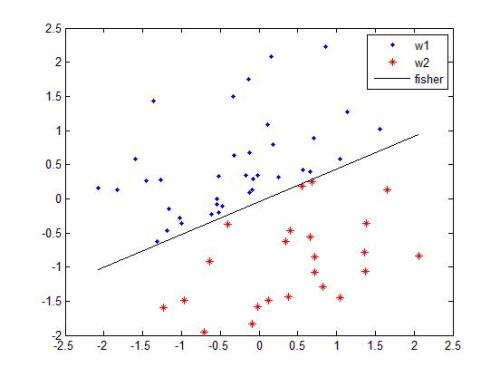
监督学习可分为分类和回归，感知器是最简单的线性分类器，现在实际应用比较少，但它是神经网络、深度学习的基本单元。

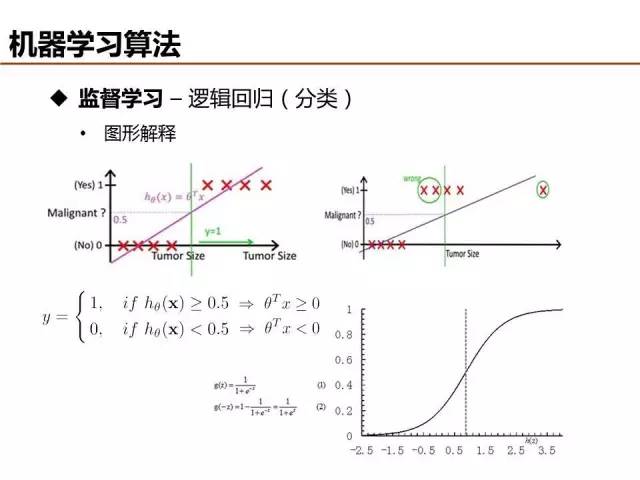
线性函数拟合数据并基于阈值分类时，很容易受噪声样本的干扰，影响分类的准确性。逻辑回归（Logistic Regression）利用 sigmoid 函数将模型输出约束在 0 到 1 之间，能够有效弱化噪声数据的负面影响，被广泛应用于互联网广告点击率预估。

逻辑回归模型参数可以通过最大似然求解，首先定义目标函数 L ( theta )，然后 log 处理将目标函数的乘法逻辑转化为求和逻辑（最大化似然概率 -> 最小化损失函数），最后采用梯度下降求解。

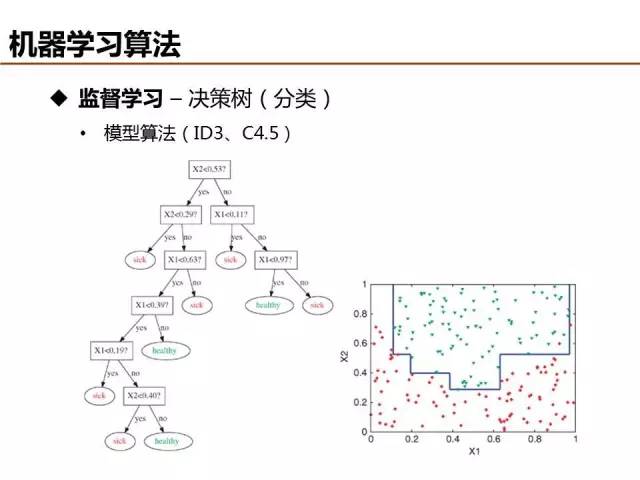
相比于线性分类去，决策树等非线性分类器具有更强的分类能力，ID3 和 C4.5 是典型的决策树算法，建模流程基本相似，两者主要在增益函数（目标函数）的定义不同。

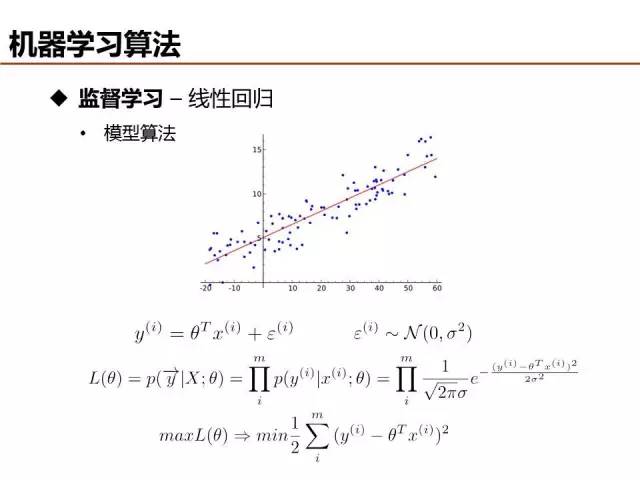
线性回归和线性分类在表达形式上是类似的，本质区别是分类的目标函数是离散值，而回归的目标函数是连续值。目标函数的不同导致回归通常基于最小二乘定义目标函数，当然，在观测误差满足高斯分布的假设情况下，最小二乘和最大似然可以等价。

当梯度下降求解模型参数时，可以采用 Batch 模式或者 Stochastic 模式，通常而言，Batch 模式准确性更高，Stochastic 模式复杂度更低。

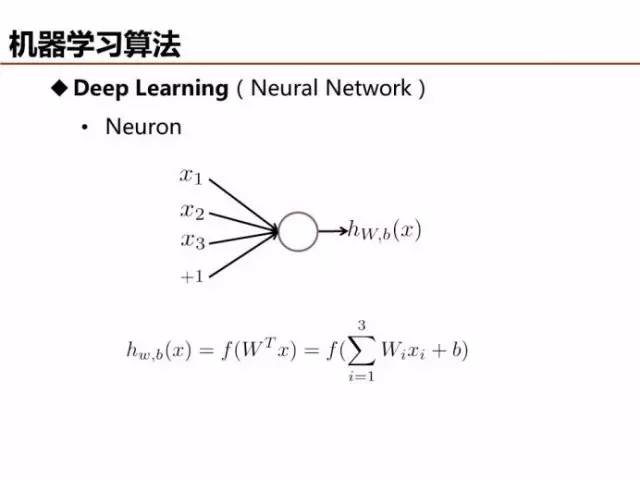
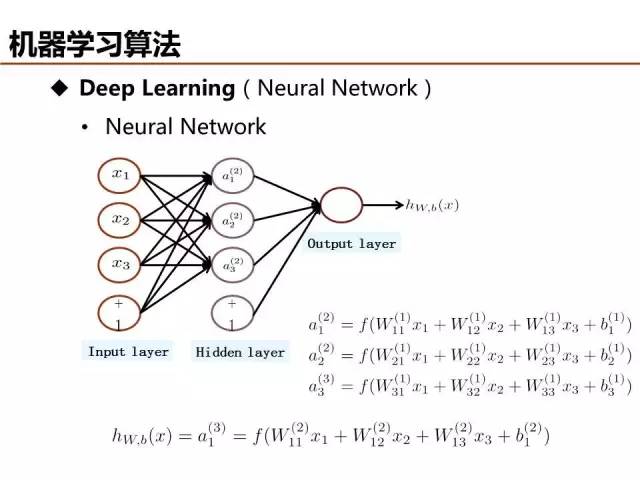
上文已经提到，感知器虽然是最简单的线性分类器，但是可以视为深度学习的基本单元，模型参数可以由自动编码（ Auto Encoder ）等方法求解。

深度学习的优势之一可以理解为特征抽象，从底层特征学习获得高阶特征，描述更为复杂的信息结构。例如，从像素层特征学习抽象出描述纹理结构的边缘轮廓特征，更进一步学习获得表征物体局部的更高阶特征。

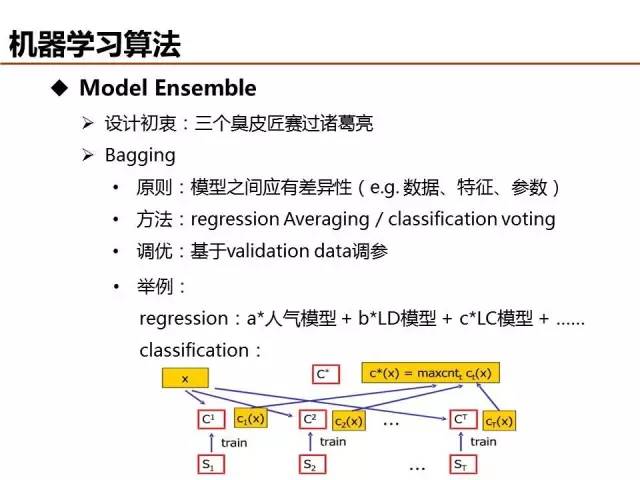
俗话说三个臭皮匠赛过诸葛亮，无论是线性分类还是深度学习，都是单个模型算法单打独斗，有没有一种集百家之长的方法，将模型处理数据的精度更进一步提升呢？当然，Model Ensembe l就是解决这个问题。Bagging 为方法之一，对于给定数据处理任务，采用不同模型/参数/特征训练多组模型参数，最后采用投票或者加权平均的方式输出最终结果。

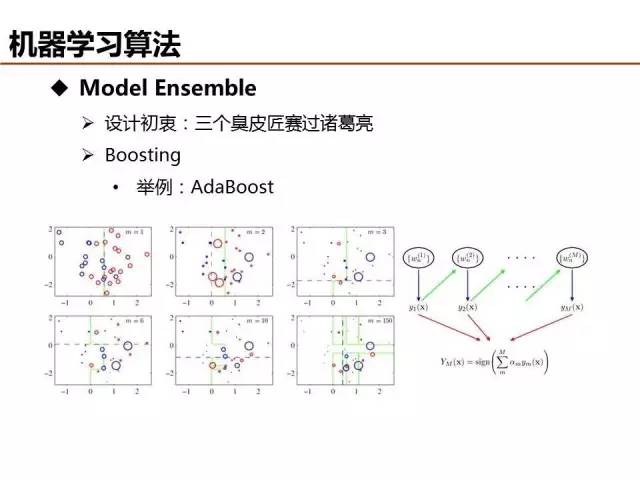
Boosting为Model Ensemble 的另外一种方法，其思想为模型每次迭代时通过调整错误样本的损失权重提升对数据样本整体的处理精度，典型算法包括 AdaBoost 、GBDT 等。

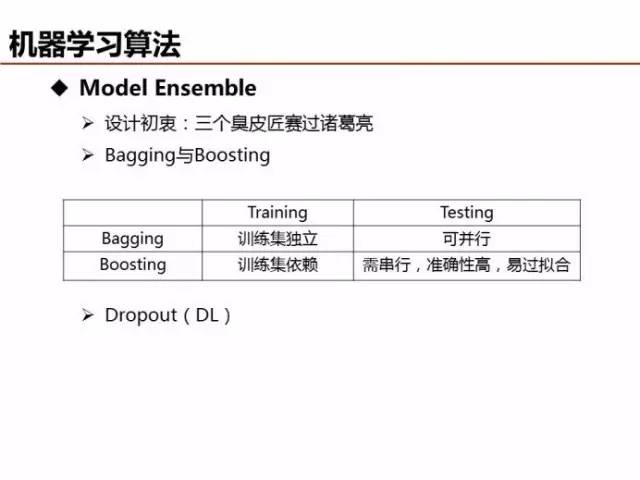
不同的数据任务场景，可以选择不同的 Model Ensemble 方法，对于深度学习，可以对隐层节点采用 DropOut 的方法实现类似的效果。

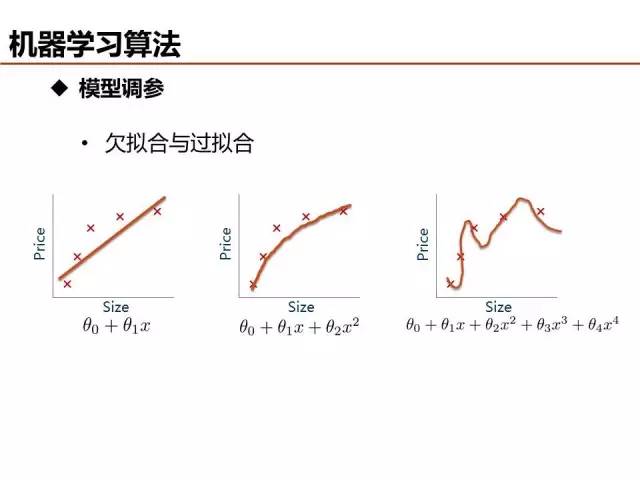
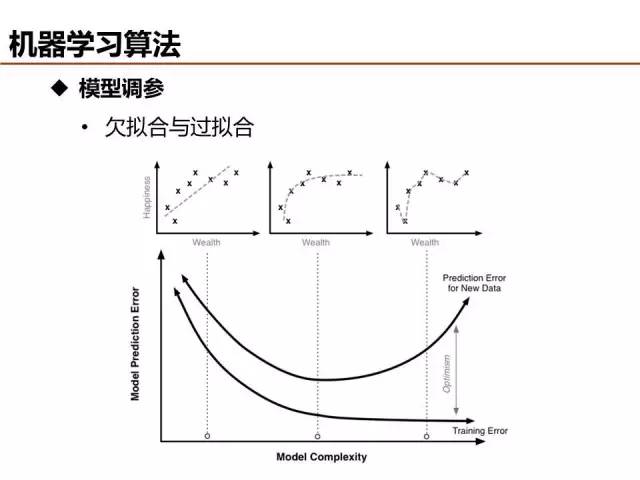
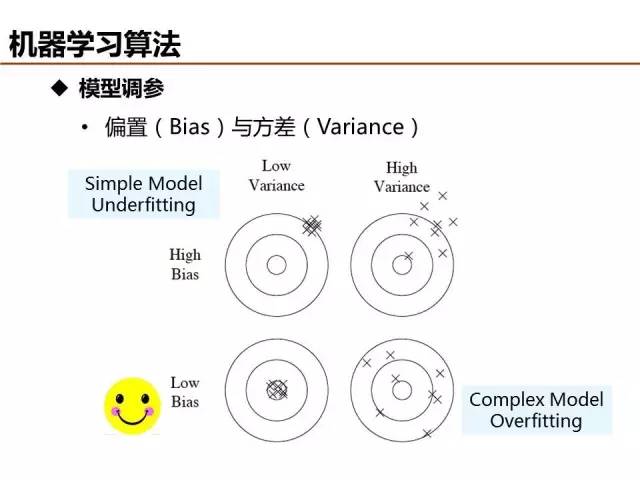
介绍了这么多机器学习基础算法，说一说评价模型优劣的基本准则。欠拟合和过拟合是经常出现的两种情况，简单的判定方法是比较训练误差和测试误差的关系，当欠拟合时，可以设计更多特征来提升模型训练精度，当过拟合时，可以优化特征量降低模型复杂度来提升模型测试精度。

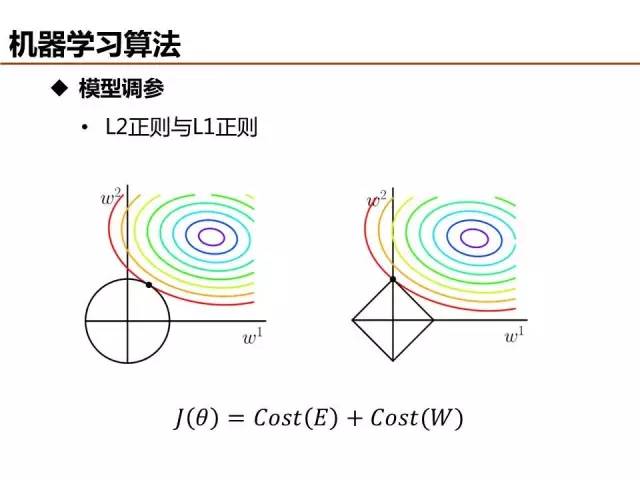
特征量是模型复杂度的直观反映，模型训练之前设定输入的特征量是一种方法，另外一种比较常用的方法是在模型训练过程中，将特征参数的正则约束项引入目标函数/损失函数，基于训练过程筛选优质特征。