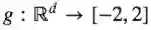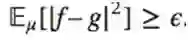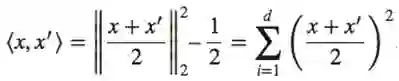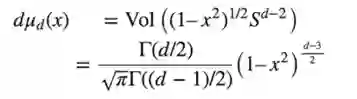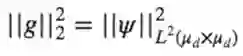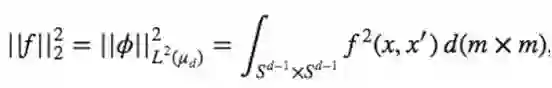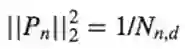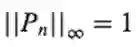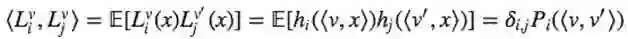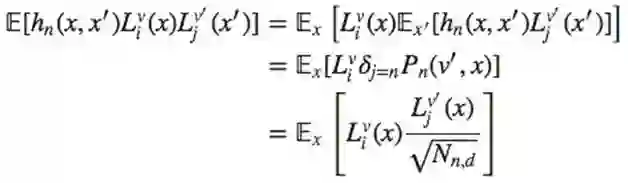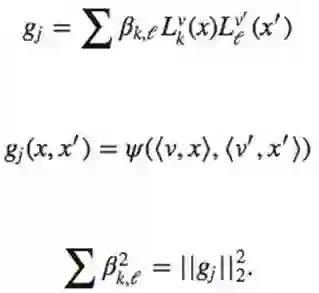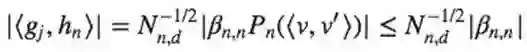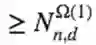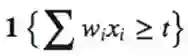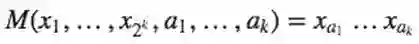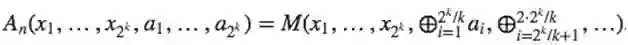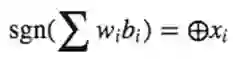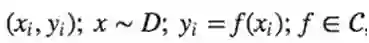深度学习数学基础第三课： 深度分离进阶 ‖ 学习

编译：黄小瓜  巴黎六大数学建模研究生

 作者：Joshua Pfeffer  推荐：@爱可可老师

---

鸡友们，有福了。小鸡接下来将为您带来深度学习数学基础系列课程，本文是第二讲。

适合人群：0-3岁的机器学习工程师

课表：

深度学习数学：讲座1-  简介及深度网络的普遍性

深度学习数学：讲座2 - 深度分离

深度学习数学：讲座3 - 深度分离+

深度学习数学：讲座4 - PAC学习与深层网络

深度学习数学：讲座5 - 随机稀疏网络等

深度学习数学：讲座6 - 简单分层模型

另外，我们也新建了深度学习课程微信群，想加入群组共同进阶的朋友请添加小鸡微信 liulailiuwang。

 

在布尔电路设置中,有一个基于深度的分离的结论：

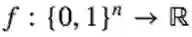
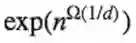
定理(Rossman,Servedio, Tan): 存在可以用深度d的由AND，OR和NOT门构成的线性公式来计算的函数，使得任何深度为d-1 的电路在输入为时可以以的大小去拟合函数f。

问题：我们可以对deepnets给出一个类似的结论么？

 

上次我们讨论了下如下的分离结果。

定理：有一个概率测度R和函数g:

－在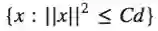被支撑，并且可以通过宽度为poly(d)的三层网络来表现。

－对于被宽度为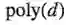的两层网络支撑的函数f，满足 

今天讨论一个更简洁的方法2或3分离结果，这个能产生更强的结果。

 

Danielly’s模型：

Danielly’s模型构造如下。从Sd-1选择统一的x和x’（例，根据Haar测度）使得f(x, x’)=g(x, x’)。输入（x，x’），深度l层的网络有以下形式：

• L = 2,  wσ(W1x + W2x’+ b1) + b2;

• L = 3, wσ(W2σ (W1x + W2x’+ b1) + b2) + b3;

现在我们证明如下定理。

 

定理：若函数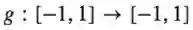是L－Lipschitz，那么存在一个三层的F可以代表f，F宽度为O(d2L/ϵ)，权重被限制在O(1+L)并且||f – F||∞<=ϵ.

这阐明了“3的魔力”。直观地，我们可以看见二次方程比线性方程更强的力量。至少对于以下这一具体方面。

 

我们可以使用以下具有一般性的深度为1的网络的辅助定理开始。

 

定理：如果f在[-R, R]区间内对于任意ϵ>0是符合L-Lipschitz条件的，那么可以选择

对f做如下近似：

|| f(x) – f(0) –αiσ(γi - βi)||∞<=ϵ, m <=

d

定理证明：重新分区间隔，注意利普希茨条件指出图像没有与直线偏离很多。

如下的章节将会给出定理的证明，并且可以给出一个更低的界。

上界

我们开始展示了函数可以被深度为3的网络很好地近似：

这说明2层网络可以很好的近似<x, x’>。我们也可以计算σ(<x, x’>)来作为一个与前面几层的线性组合。这与定理的相结合可以给出我们期望的结论2.。

 

下界

我们也想展示一个可以很好近似方程的深度2的网络宽度会很大。我们通过思考下面的问题来分析：

 

问：什么是<x, x’>的分布？

近似：旋转不变性指出：

D(<x, x’>) = D’(<x,r>) = D(<x, e1>) = D(x1)

注意着对于确定的x’，和随机的x那么这个结论也是正确的。

均匀分布的随机向量的独立元<x, ek>在时可以近似高斯分布。一个在统一的随机向量在x接近高斯d——>的个体组成。当然，

是t-statistic分布（在会逼近向高斯分布）。如果其中一个向量x, x’是固定的，也有同样的结论。因此，如果g = ψ(<v,x>,<v^',x'>)，那么

并且若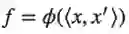，那么

 

这里d(m*m)表示Haar测度。

 

正交多项式：定义P0 = 1, P1 = x, Pn = (2n+d-4)/(n+d-3)·Pn-1(x) –(n-1)/(n+d-3) · Pn-2(x)

我们观察得到：

这里有

，

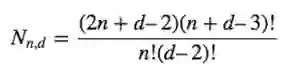
现在定义

，

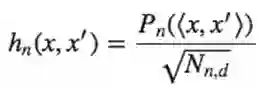
以下事实是解决问题的关键：

也就相当于

做形式变换有：

 

更低下界的想法：

现在我们讨论下怎样得到想要的更低的下界。

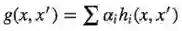
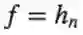
扩展并且选择“噪声敏感”f是。例，有很多更高的傅立叶等级的噪声。 其他的证明还需要假设对于一个较大的n有（尽管hn是一个Lip函数，但是我们可以找到一个在更高等级上有很多权重的函数）。

 

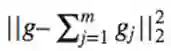
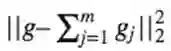
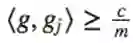
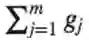
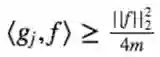
我们想要或bj在时足够大。否则，存在一个j使得。注意到如果hn和接近，那么我们需要至少有一个j在这个j上有。

现在我们计算<gj,f>，观察得到

因此，

所以m足够大或者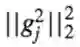足够大。注意，没有以下两点那么我们得到的近似就是不好的：

-宽度

或

-最大权重

开放性问题： 1大的权重就可以解决近似问题吗？2不用Haar测度，这个近似可以直接在Gaussian空间被计算吗？我们失去了旋转不变量,但奇怪的是是我们用接近高斯测度的测度不能直接在高斯空间里证明它。

 

Kane-Williams模型

阀值门定义如下：

 

定理：存在函数可以被计算如下：

 

-用O(n)门的3层阀值电路

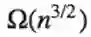
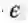
-但是要求由2层电路输入时，保证至少的门在.5+上准确计算

 

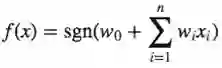
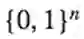
基本的单元阀值是我们假定一个在上的均匀分布。

 

Meta-问题：我们可以利用模型(例，之前的结论)之间的约简来得到一个二元问题的更好的分离吗？

 

不完全回答：由复杂性理论，比poly(n)更好是不可能的。

 

问：我们可以用之前的结论代替新的激活吗？

 

证：首先定义函数

是一个Mux函数生成。然后

这里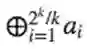是这段字符串的奇偶校验位。

要求1:M可以被深度2用的门计算。

要求2:奇偶性可以被阀值门计算。

要求2的证明：令

赋予权重w1…wn可以有

事实上，这个可以用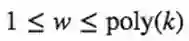解决，我们就不在这说了。

 

现在我们向更低的界做进一步了解。

 

定理：对于除了的所有Boolean函数，没有大小小于的深度2 的网络可以在输入比多时拟合函数f。

 

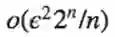
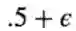
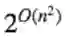
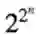
定理的简单证明：阀值函数的数量小于，但是函数的总量是。

就是说一般没有那么多阀值函数。并且，对于多数在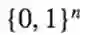的Boolean函数f，一个2层的大小的网络不能很好近似f。

会到定理的证吗上，这个想法是生成一个随机函数，允许我们引用多数函数不能很好的近似f这个定理。这里有结论：

• 随机得到一个x

• 对每个模块ai，除了一个坐标随机外，固定所有坐标

• 生成一个k个变量的随机函数

 

问：一个通过随机给定所有位的2层的网络是什么样的？

直观回答：一旦足够的位固定好了，多数门会变成常数然后死掉。然后我们留下一个更小的不能很好近似f的网络。

主要定理：一个随机逻辑限制门可以在至少为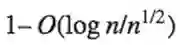概率下给出一个常函数。

 

因此，仍然存在的门的数量是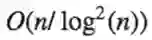，这个数量不足以表示一个随机函数。

 

PAC学习

我们要用PAC学习的定义来结束这门课。我们有一个Xn空间并且想研究函数

。令C为这些函数的类。

 

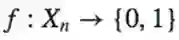
定义： C是对于所有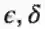，所有Xn上的分布D为PAC可学习的类。存在一个算法A使得给定样本：

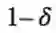
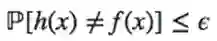
有大于的概率，A返回一个函数使得并且A在里运行。

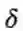
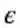
这里，是一个全局参数，是概率误差。

★推荐阅读★

用机器学习和大数据来预测心脏病（代码）

哈佛科学家研发出神奇“胶水”，几分钟让伤口愈合

李飞飞：ImageNet证明深度学习需要海量数据支持

重磅 ‖ 一篇文章畅行自动驾驶，全维度资源合集

干货 ‖ 入门数据科学的65个免费资源

加入「AI从业者社群」请备注个人信息，添加小鸡微信  liulailiuwang