象棋人工智能算法的C++实现（五）——人机博弈的高阶算法

点击上方“程序人生”，选择“置顶公众号”

第一时间关注程序猿（媛）身边的故事

作者

De掉所有bug

如需转载，请联系原作者。

上一期博客介绍了最为简单的人机博弈算法，包括获取所有合法路径、简单的估值以及电脑走棋。本期博客的进阶之处在于，所介绍的估值算法是建立在上一期博客的简单估值函数基础上的极大极小值算法（Minimax算法）。

象棋人工智能算法的C++实现（四）——人工智能的开端

象棋人工智能算法的C++实现（三）——注重功能分区！！！

象棋人工智能算法的C++实现（二）

象棋人工智能算法的C++实现（一）

关于极大极小值算法：

极大极小值算法是一种找出失败的最大可能性中的最小值的算法（即最小化对手的最大得益）。举个例子，电脑为A，人类为B，A在走棋之前需要思考，A走了某一步后，看看B有哪些走法，B又不傻，所以B肯定是要选择让A得分最少的走法走棋，而A就是在A的所有走法中选择B给出的让A得分最少的走法中得分最多的走法。听起来大概会比较抽象比较绕吧，试着多读几遍，多理解理解。

给电脑配置极大极小值算法让电脑选择走棋路径大概分3步走（还是电脑为A，人类为B）：

1.在当前局面下获取A的所有走棋路径，并试着走一下。

2.在上一步（A已经试着走了一下）的基础上获取B的所有走棋路径，并以B的视角试着走一下，然后评估局面分（因为A是电脑，所以局面分是以A的角度计算的，即A的总分-B的总分），遍历完B的所有走棋路径后返回这些局面分中的最小值（对A最不利而对B最有利）。

3.在上一步返回的局面分的最小值中，找到最大值，并锁定与该最大值对应的走棋路径作为返回值返回。

因为现今既需要获取电脑的所有走棋路径又需要获取人类的所有走棋路径，所以对getAllPossibleMove函数稍微修改一下：

//获取所有走的通的走法存放在数组steps里
void SingleGame::getAllPossibleMove(QVector<Step *>& steps)
{
    int min=16,max=32;
    if(this->_bRedTurn)
    {
        min=0,max=16;
    }
    //遍历所有棋子
    for(int i=min;i<max;i++)
    {
        //如果棋子已死则直接跳过
        if(_s[i]._dead) continue;
        //遍历所有行坐标
        for(int row=0;row<=9;row++)
        {
            //遍历所有列坐标
            for(int col=0;col<=8;col++)
            {
                //获取想要杀死的棋子的id
                int killid=this->getStoneId(row,col);
                //若想要杀死的棋子与行走的棋子颜色相同则跳过
                if(sameColor(killid,i)) continue;
                //判断某一棋子能不能行走
                if(canMove(i,killid,row,col))
                {
                    //将可以行走的“步”存放到steps中
                    saveStep(i,killid,row,col,steps);
                }
            }
        }
    }
}

相比上一期博客，getBestMove函数不再直接调用估值函数，而是调用了getMinScore函数以找到对A最不利而对B最有利的分值。

上getBestMove函数的源代码：

//获取最优走法
Step* SingleGame::getBestMove()
{
    QVector<Step *> steps;
    //获取电脑的所有走棋路径
    getAllPossibleMove(steps);
    int maxScore=-100000;
    Step* ret;
    for(QVector<Step*>::iterator it=steps.begin();it!=steps.end();++it)
    {
        Step* step=*it;
        //试着走一下
        fakeMove(step);
        //获取电脑当前走法下对自己最不利的分值
        int score=getMinScore();
        //再走回来
        unfakeMove(step);
        //从所有对自己最不利的分值中找到对自己最有利的分值并锁定走棋路径作为返回值返回
        if(score>maxScore)
        {
            maxScore=score;
            ret=step;
        }
    }
    return ret;
}

上getMinScore函数的源代码：

int SingleGame::getMinScore()
{
    QVector<Step*> steps;
    //获取人类的所有走棋路径
    getAllPossibleMove(steps);
    int minScore=100000;
    for(QVector<Step*>::iterator it=steps.begin();it!=steps.end();++it)
    {
        Step* step=*it;
        //以人类的视角试着走一下
        fakeMove(step);
        //评估局面分
        int score=calcScore();
        //再走回来
        unfakeMove(step);
        //找到对电脑最不利的分数作为返回值返回
        if(score<minScore)
        {
            minScore=score;
        }
    }
    return minScore;
}

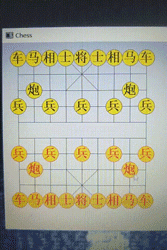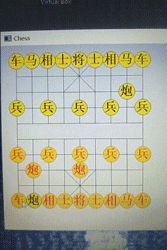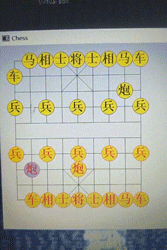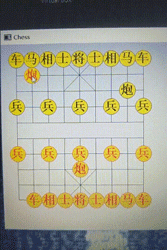
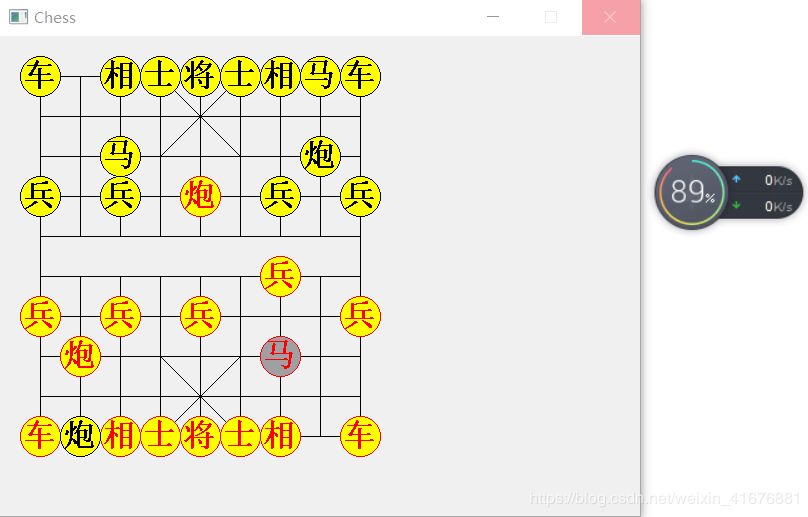
到目前为止，象棋人工智能的效果是这样的： 

能够看出来，电脑变得比之前更聪明了。我吃掉它的炮后，它出了车，我把炮放在它眼前，它反而不吃，因为它知道我是在拿我的炮钓它的车。 这便是“走一步看两步”的两步人工智能。

那么问题来了，如何实现“走一步看三步”的三步人工智能乃至更多步人工智能呢？可以用递归的思想改写上面介绍的getBestMove函数和getMinScore函数，然后再加一个递归的getMaxScore函数，还需要在SingleGame类中加一个数据成员_level来表示递归的层数（当然递归的层数越大电脑越聪明）。

写一个SingleGame类的构造函数来将_level初始化：

SingleGame::SingleGame()
{
    _level=3;
}

上getMaxScore函数的源代码：

int SingleGame::getMaxScore(int level)
{
    if(level==0) return calcScore();
    QVector<Step*> steps;
    getAllPossibleMove(steps);
    int maxScore=-100000;
    for(QVector<Step*>::iterator it=steps.begin();it!=steps.end();++it)
    {
        Step* step=*it;
        fakeMove(step);
        int score=getMinScore(level-1);
        unfakeMove(step);
        if(score>maxScore)
        {
            maxScore=score;
        }
    }
    return maxScore;
}

getMaxScore函数可以仿照getMinScore函数写，他们两个的区别就在于返回最大值还是返回最小值。 

上改写后的getMinScore函数的源代码：

int SingleGame::getMinScore(int level)
{
    if(level==0) return calcScore();
    QVector<Step*> steps;
    getAllPossibleMove(steps);
    int minScore=100000;
    for(QVector<Step*>::iterator it=steps.begin();it!=steps.end();++it)
    {
        Step* step=*it;
        fakeMove(step);
        int score=getMaxScore(level-1);
        unfakeMove(step);
        if(score<minScore)
        {
            minScore=score;
        }
    }
    return minScore;
}

上改写后的getBestMove函数的源代码：

Step* SingleGame::getBestMove()
{
    QVector<Step *> steps;
    //看看有哪些步骤可以走
    getAllPossibleMove(steps);
    int maxScore=-100000;
    Step* ret;
    for(QVector<Step*>::iterator it=steps.begin();it!=steps.end();++it)
    {
        Step* step=*it;
        //试着走一下
        fakeMove(step);
        int score=getMinScore(_level-1);
        unfakeMove(step);
        if(score>maxScore)
        {
            maxScore=score;
            ret=step;
        }
    }
    return ret;
}

大家注意！！！_level的值不要设置太大。我测试过，我的电脑4G内存，_level设置为4前期还可以勉强运行（运行速度特别慢），后期剩下的棋子越来越少，每个活着的棋子行走的选择就会越来越多，因此占的内存会越来越大，直到程序崩溃。不知道8G内存的电脑情况如何，大家可以自行测试一下。

_level设置为4，后期电脑思考时飙升的内存占用：

再后期程序会异常结束。

毕竟最佳走棋路径是穷举出来的，消耗内存是避免不了的，还请各位大佬勿喷。

到目前为止，象棋的基础人工智能算法算是讲完了。然而，后期更深度的优化还有好多。如果反响比较强烈，我会选择继续更新。

- The End -

「若你有原创文章想与大家分享，欢迎投稿。」

加编辑微信ID，备注#投稿#：

程序 丨 druidlost  

小七 丨 duoshangshuang

点文末阅读全文，看『程序人生』其他精彩文章推荐。

推荐阅读：

• 90 后篮球运动员成功转型 iOS 开发，过程超刺激
  

• 为什么程序员恨死了康熙的这位儿子？

• 算法工程师独得恩宠 四面楚歌的Android工程师该何去何从？
  

• 算力寻租或将终结中本聪的POW机制？深度解析BCH“司机补贴战”
  

• Python告诉你：这类程序员最赚钱！
  

• 公开课报名 | 详解CNN-pFSMN模型以及在语音识别中的应用

• Java 程序员必备的 15 个框架，前 3 个地位无可动摇！

print_r('点个赞吧')；
var_dump('点个赞吧')；
NSLog(@"点个赞吧！")
System.out.println("点个赞吧!");
console.log("点个赞吧!");
print("点个赞吧!");
printf("点个赞吧!\n");
cout << "点个赞吧!" << endl;
Console.WriteLine("点个赞吧!");
fmt.Println("点个赞吧!")
Response.Write("点个赞吧")；
alert（’点个赞吧’）