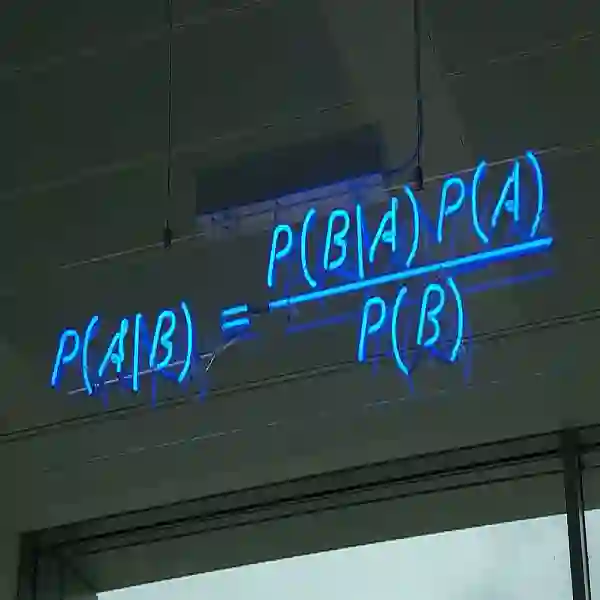上帝手中的骰子——无所不能的贝叶斯(下篇)
本文为量子金服原创文章,转载须授权
在《上帝手中的骰子——无所不能的贝叶斯(上篇)》中,我们从贝叶斯定理开始,讲述了贝叶斯公式和它在早期两个非常重要的应用事件。如今,贝叶斯理论在数学及工程领域应用极其广泛,那么到底是什么事件重新让它突破应用的障碍,重新受到科学家们重视的呢?今天,笔者将从贝叶斯理论最重要的应用说起,看看它究竟是如何大放异彩的。
贝叶斯理论的伯乐
▲Frederick Jelinek
千里马常有,而伯乐不常有。谈起贝叶斯公式的应用,就不得不提起一个人——语音和语言处理大师Fred Jelinek,没有他,人们不知到多久以后才会知道语言还能被机器处理。
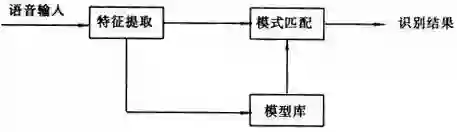
人们平时在说话时,脑子就是一个信息源。人们的喉咙(声带),空气,就是如电线和光缆般的信道。听众耳朵的就是接收端,而听到的声音就是传送过来的信号。根据声学信号来推测说话者的意思,就是语音识别。这样说来,如果接收端是一台计算机而不是人的话,那么计算机要做的就是语音的自动识别。同样,在计算机中,如果我们要根据接收到的英语信息,推测说话者的汉语意思,就是机器翻译;如果我们要根据带有拼写错误的语句推测说话者想表达的正确意思,那就是自动纠错。
在70年代以前,语音识别还停留在识别小词汇量、孤立词的方面
1973年,贾里尼克在IBM组建了语音识别的研究队伍,其中包括他的著名搭档波尔(Bahl),著名的语音识别 Dragon 公司的创始人贝克夫妇,解决最大熵迭代算法的达拉皮垂(Della Pietra)孪生兄弟,BCJR 算法的另外两个共同提出者库克(Cocke)和拉维夫(Raviv),以及第一个提出机器翻译统计模型的布朗。
在贾里尼克以前,科学家们把语音识别问题当作人工智能问题和模式匹配问题:
贾里尼克把它当成通信问题,他通过将贝叶斯公式和马尔科夫链结合,简化问题使计算机能够方便求解,从而解决了语音识别问题。
N-Gram是大量词汇连续语音识别中最常见的一种语言模型,模型基于独立输入假设:第n个词的出现只与前面N-1个词相关,而与其它任何词都不相关,整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计N个词同时出现的次数得到。这个是个基于贝叶斯公式的统计语言模型。
贾里尼克对至今的语音和语言处理有着深远的影响,他的研究从根本上使得语音识别有实用的可能。自此之后,贝叶斯方法的应用延伸到各个问题领域,所有需要作出概率预测的地方都可以见到贝叶斯方法的影子,如今,贝叶斯更是机器学习的核心方法之一。
“聪明的”贝叶斯分类器
我们都知道贝叶斯方法曾有200年无人问津,原因是经典统计学完全能够解决小型问题,而且相比需要靠主观判断的贝叶斯方法,建立在客观事实上的经典统计学更让人信服。但随着大型问题的出现,经典统计学在面对复杂问题时,往往无法获得足够多的样本数据,导致其无法通过研究样本来推断总体规律。数据的稀疏性令经典统计学频频碰壁,直到计算机技术的飞速发展后,数据的大量运算变得可能,贝叶斯方法这才被人重新重视起来。
我们以多分类任务为例,来解释贝叶斯决策的基本原理:
假设有N种可能的类别标记,即Y={c1,c2,...,cN},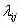
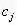
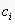
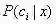
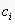
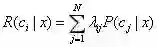
我们的任务是寻找一个判定准则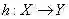
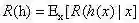
显然,对每个样本x,若h能最小化条件风险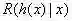
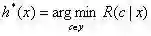
此时,h*称为贝叶斯最优分类器(Bayes optimal classifier),与之对应的总体风险R(h*)称为贝叶斯风险(Bayes risk),1-R(h*)反映了分类器所能达到的最好性能,这也是通过机器学习所能产生的模型精度的理论上线。(更多内容,可参考《机器学习》周志华著)
正确识别垃圾邮件的技术难度非常大,传统方法有:
关键词法:根据特定关键词过滤邮件
邮件特征过滤法:根据邮件的某些特征,如语言、文件格式等判断是否为垃圾邮件
校验码法:计算文本的校验码,再与抑制的垃圾邮件进行对比
但这些方法识别效果并不理想,很容易规避。
2002年,Paul Graham提出用“贝叶斯推断”过滤垃圾邮件,结果这样做的效果好的不可思议,1000封垃圾邮件可以过滤掉995封,且没有一个误判。
可以看出贝叶斯分类器是一种统计学分类器,建立在已有的统计结果之上,我们必须预先提供两组已经识别好的邮件,一组是正常邮件,而另一组是垃圾邮件。以这两组邮件对分类器进行训练,邮件的规模越大,训练的效果就越好
这种分类器具有自我学习的功能,所以贝叶斯分类器被广泛应用在人工智能、心理学、遗传学、模式识别等领域。
贝叶斯决策论在机器学习,模式识别等诸多关注数据分析的领域都有极为重要的地位,对贝叶斯定理进行近似求解,为机器学习算法的涉及提供了一种有效途径。
根据对属性间依赖的涉及程度,贝叶斯分类器形成了一个谱:从朴素贝叶斯分类器(不考虑属性间依赖性)到贝叶斯网(表示任意属性间依赖性),二者之间是一系列半朴素贝叶斯分类器。它们各有所长,针对某些特定问题有着非常显著的效果。
比如朴素贝叶斯分类器:它引入了属性条件独立性假设,这个假设其实在现实应用中很难成立,但是许多情形下并不影响朴素贝叶斯分类器的性能,在信息检索领域十分常用。
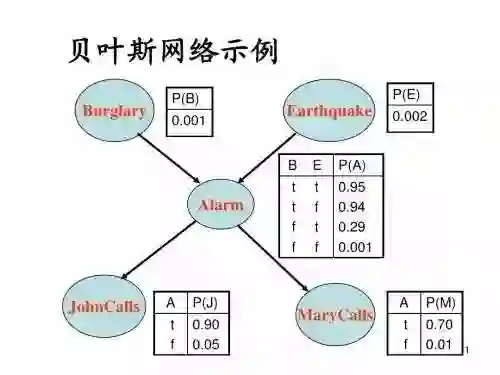
又如贝叶斯网:它借助有向无环图来刻画属性间的依赖关系,为不确定学习和推断提供了基本框架。它比马尔科夫链灵活,更适合解决复杂问题,未来随着量子计算机的发展,贝叶斯网络进行迭代训练的计算问题将会得到解决,届时,贝叶斯网一定能在人工智能领域大放异彩。
最简单的贝叶斯定理,到复杂的贝叶斯网,回头来看,现在的许多算法都是许多年前就已经出现的,数学的神奇可见一斑。写到这里,我们再回头看看文章最开始讲的贝叶斯定理:
P(A|B)=P(AB)/P(B)
就会发现,原来机器学习的智慧,最初竟是如此简单的模样。
- END -