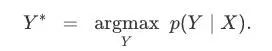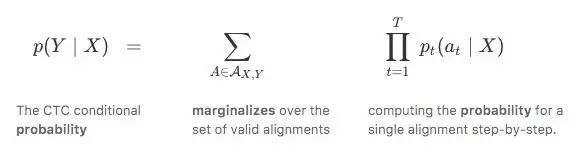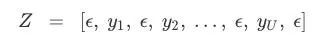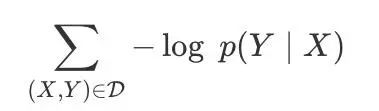吴恩达学生Awni Hannun：图文演示如何用CTC进行序列建模（上）

编译：Bot

来源：distill

编者按：CTC是一种训练语音识别DNN模型的算法，它是一种端到端的工具，现已被广泛应用于语音信息解码等实际领域。近日，斯坦福博士Awni Hannun在机器学习平台distill上发表了一篇教程，演示如何用CTC进行序列建模。据了解，Awni Hannun师承吴恩达，曾任跟随导师任百度硅谷AI实验室语音识别小组研究员（负责人），并是2014年突破性语音识别成果“Deep Speech”的主要参与者之一。

以下是经论智编译的原文：

CTC识别效果示意图

简介

谈及语音识别，如果这里有一个剪辑音频的数据集和对应的转录，而我们不知道怎么把转录中的字符和音频中的音素对齐，这会大大增加了训练语音识别器的难度。

如果不对数据进行调整处理，那就意味着不能用一些简单方法进行训练。

对此，我们可以选择的第一个方法是制定一项规则，如“一个字符对应十个音素输入”，但人们的语速千差万别，这种做法很容易出现纰漏。为了保证模型的可靠性，第二种方法，即手动对齐每个字符在音频中的位置，训练的模型性能效果更佳，因为我们能知道每个输入时间步长的真实信息。但它的缺点也很明显——即便是大小合适的数据集，这样的做法依然非常耗时。

事实上，制定规则准确率不佳、手动调试用时过长不仅仅出现在语音识别领域，其他工作，如手写识别、在视频中添加动作标记，同样会面对这些问题。

手写识别：输入的坐标由笔画/像素在图中位置决定；语音识别：输入可以是声谱图或是基于其他频率提取的特征

在这种情况下，联结主义时间分类器（Connectionist Temporal Classification），又名CTC，是一种让网络自动学会对齐的好方法，它十分适合被用于语音识别和书写识别。

为了描述地更形象一些，我们可以把输入序列（音频）映射为X=[x1,x2,…,xT]，其相应的输出序列（转录）即为Y=[y1,y2,…,yU]。这之后，将字符与音素对齐的操作就相当于在X和Y之间建立一个准确的映射。

如果想直接用非监督学习算法，我们还有3个难点：

• X和Y的长度是可变化的；

• X和Y的长度比例也是可变化的；

• X和Y没有严格对齐。

而CTC算法刚好能解决这些问题，给定一个X，它能基于所有可能是准确映射的Y给出输出分布。根据这个分布，我们可以推理最可能的输出，或计算分布内各字符的可能性概率。

CTC在计算loss和inference上十分高效：

损失函数：为了给出准确的输出，经训练的模型必须在分布中最大化正确输出的概率，为此，我们需要计算概率p(Y|X)（输入X后输出为Y的概率），这个p(Y|X)应该是可微的，所以才能使用梯度下降法。

Inference：一般而言，如果已经训练好了一个模型，我们就应该针对输入X推理一个可能的Y，这就意味着要解决这个问题：

理想情况下，这个Y*可以被快速找到。有了CTC，就意味着我们能在低投入情况下迅速找到一个近似的输出。

算法

CTC算法可以根据输入X映射一些带有概率的Y，而计算概率的关键在于算法如何看待输入和输出之间的一致性。在讨论它是如何计算loss和进行inference前，我们先来看一下什么叫对齐。

对齐

CTC算法不要求输入和输出的严格对齐，但是为了计算概率大小，总结两者的一些对齐规律的必要的，这之中涉及一些loss计算。

为了激发CTC的特定形式，我们可以实验一个简单的例子。假设输入X长度为6，输出Y=[c, a, t]，那么对齐X和Y的一种有效方法是为每个输入长度分配一个输出字符并重复collapse：

这样做会出现两个问题：

• 通常情况下，强制要求输入与输出的严格对齐是没有意义的。例如在语音识别中，输入可以有一些静音，但模型不必给出相应的输出；

• 无法产生连续多个相同字符。如果输入是[h, h, e, l, l, l, o]，CTC会折叠重复的字符输出“helo”，而不是“hello”。

为了解决这些问题，CTC加入了一个空白符号——blank。在这个语音识别问题里，我们暂时把它设为ϵ，它不对应任何输入，最后会从输出中被删除。

由于CTC允许路径长度和输入长度等长，映射到Y的相邻ϵ可以合并整合，最后统一去除：

如果Y在同一行中的相邻位置有两个相同的字符，为了做到有效对齐，它们之间必须插入一个空白符号ϵ。有了这个规则，模型才能准确区分collapse到“hello”的路径和collapse到“helo”的路径。

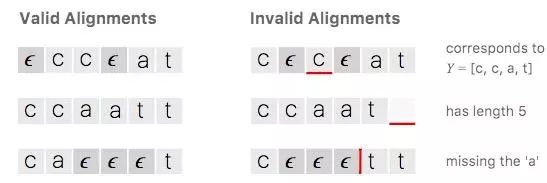
让我们回到之前[c, a, t]的例子，以下是它的两个无效对齐示例：

可以发现，CTC选择的路径有一些明显的性质。首先，整个对齐过程是单调（monotonic）的，如果我们前进到下一个输入，输出会保持现状或显示下一个输出；其次，X到Y的对齐形式是多对一，一个或多个输入只能对齐到一个输出。第三，由第二个特征可得，输出Y的长度不得大于输入X。

损失函数

CTC的对齐方式展示了一种利用时间步长概率推测输出概率的方法。

确切地说，如果CTC的目标是一对输入输出(X,Y)，那Y的路径的概率之和为：

Y的概率；所有可能路径概率求和；逐个计算单个路径概率

用CTC训练的模型通常用递归神经网络（RNN）来预测每个时间步长概率：pt(at|X)。由于RNN能考虑输入中的上下文，它的表现可圈可点，但我们也可以自由选用一些学习算法，让算法在给定固定输入片段的情况下产生输出分布。

当然，如果操作不当，CTC计算loss占用的资源会很惊人。一种简单的方法是逐一计算每种对齐路径的概率，之后再进行求和，但它的缺点是路径数量往往非常惊人，这样做对于大多数任务来说太慢了。

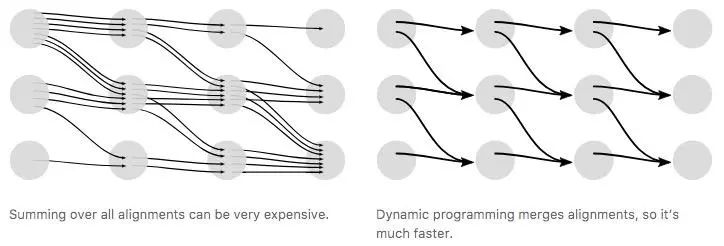
值得庆幸的是，我们能用动态规划算法快速计算loss，其关键思路是如果两种路径用相同步长映射到同一输出，那它们就能被合并。

左：总结所有路径会占用大量资源；右：动态规划算法合并了路径，计算更快

因为CTC允许在Y中的字符前任意加入ϵ，所以为了更直观地描述算法，我们可以把输出序列设为：

设α为相同对齐路径合并后的CTC得分（概率），更准确地说，即αs,t是输入t后子序列Z1:s的得分。可以发现，如果要获得p(Y|X)，我们可以从α最后那个时间步长开始计算。只要能算出最后时间步长时α的值，我们就能得到αs,t。以下是两个示例：

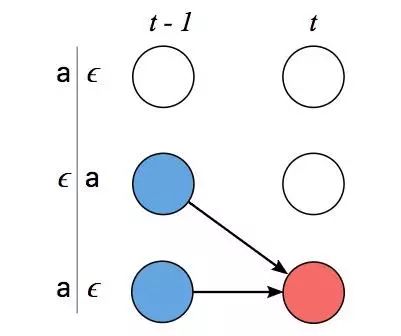
• 例1

如上图所示，在这种情况下，我们不能跳过zs−1，它是Z之前的标记内容，所以可能是一个映射Y。由于之前我们设Z=[ϵ, y1, ϵ, y2,…,ϵ, yU, ϵ]，每个Y前后都有一个blank，因此可以推断出zs=ϵ，同理，zs=zs−2。

为了保证没有跳过zs−1，我们可以利用之前的时间步长进行计算：

第t-1个输入时输出对齐路径CTC得分；第t个输入时当前路径的概率

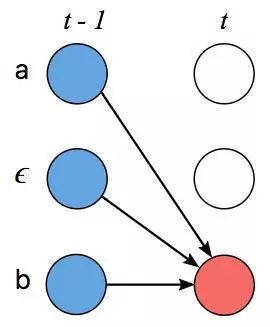
• 例2

在上图中，由于zs−1介于两个ϵ之间，因此我们可以跳过Z之前的标记，这样之后，我们计算得分的方法就变成了这样：

第t-1个输入时之后3个有效子序列的CTC得分；第t个输入时当前路径的概率

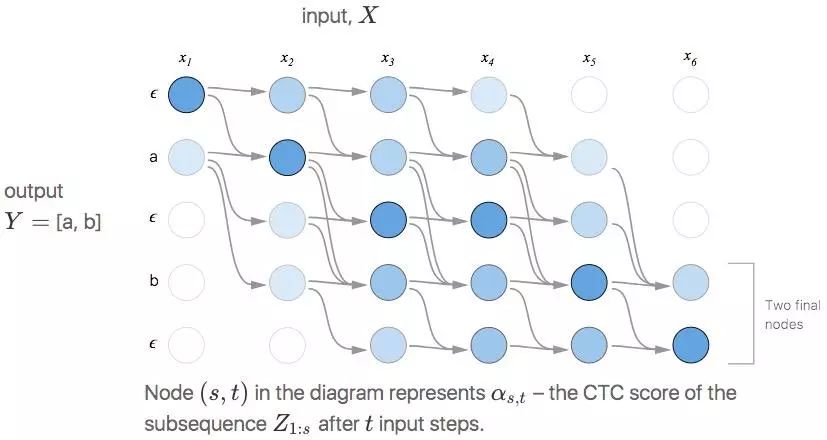
以下是一个用动态编程算法执行计算的示例，在这幅图中，每个有效对齐都有一条路径。

(s,t)表示第t个输入时Z1:s的CTC得分αs,t

如上图所示，它有两个有效起始节点和两个最终节点，总概率即两个最终节点之和。

现在我们可以有效地计算损失函数，下一步就是计算一个梯度并训练模型。CTC损失函数对于每个时间步长输出概率是可微的，因为它只是它们的总和和乘积。鉴于此，我们可以分析计算相对于（非标准化）输出概率的损失函数的梯度，并像往常那样从那里运行反向传播。

对于训练集D，模型参数先要调整以使负对数似然值最小化：

而不是直接使似然值最大化。

(未完待续……）