【ResNet】ResNet到底在解决一个什么问题呢？

会员服务 ·

【ResNet】ResNet到底在解决一个什么问题呢？

2020 年 5 月 3 日 深度学习自然语言处理

点击上方，选择星标或置顶，每天给你送干货！

阅读大概需要20分钟

跟随小博主，每天进步一丢丢

编辑：Amusi（CVer） | 来源：知乎

https://www.zhihu.com/question/64494691

本文仅作为学术分享，如果侵权，会删文处理

插播：

进入该链接留言送5本书：

《深度学习训练营 21天实战TensorFlow+Keras+scikit-learn》

最近看到不少ResNet的变体，比如ResNeSt、IResNet等。虽然ResNet发布于2015年，但目前仍有大量CV任务用其作为backbone。

截止2020年5月1日，ResNet的引用量已达到44224（数据来自谷歌学术），本文就来深入探讨一下强悍的ResNet。

Resnet到底在解决一个什么问题呢？

既然可以通过初试化和归一化（BN层）解决梯度弥散或爆炸的问题，那Resnet提出的那条通路是在解决什么问题呢？

在He的原文中有提到是解决深层网络的一种退化问题，但并明确说明是什么问题！

作者：王峰
https://www.zhihu.com/question/64494691/answer/220989469

17年2月份有篇文章，正好跟这个问题一样。

The Shattered Gradients Problem: If resnets are the answer, then what is the question?

大意是神经网络越来越深的时候，反传回来的梯度之间的相关性会越来越差，最后接近白噪声。因为我们知道图像是具备局部相关性的，那其实可以认为梯度也应该具备类似的相关性，这样更新的梯度才有意义，如果梯度接近白噪声，那梯度更新可能根本就是在做随机扰动。

有了梯度相关性这个指标之后，作者分析了一系列的结构和激活函数，发现resnet在保持梯度相关性方面很优秀（相关性衰减从到了）。这一点其实也很好理解，从梯度流来看，有一路梯度是保持原样不动地往回传，这部分的相关性是非常强的。

作者：灰灰
https://www.zhihu.com/question/64494691/answer/271335912

一方面: ResNet解决的不是梯度弥散或爆炸问题，kaiming的论文中也说了:臭名昭著的梯度弥散/爆炸问题已经很大程度上被normalized initialization and intermediate normalization layers解决了;

另一方面: 由于直接增加网络深度的(plain)网络在训练集上会有更高的错误率，所以更深的网络并没有过拟合，也就是说更深的网络效果不好，是因为网络没有被训练好，至于为啥没有被训练好，个人很赞同前面王峰的答案中的解释。

在ResNet中,building block:

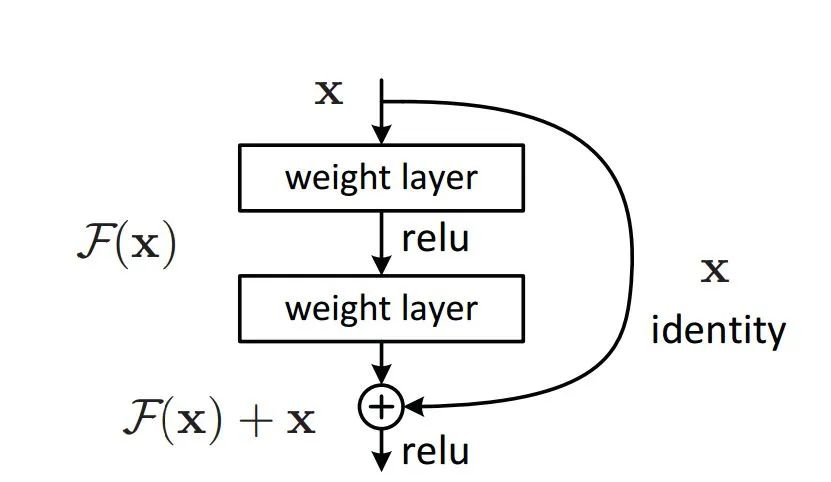
H(x)是期望拟合的特征图,这里叫做desired underlying mapping

一个building block要拟合的就是这个潜在的特征图

当没有使用残差网络结构时,building block的映射F(x)需要做的就是拟合H(x)

当使用了残差网络时,就是加入了skip connection 结构,这时候由一个building block 的任务由: F(x) := H(x)，变成了F(x) := H(x)-x

对比这两个待拟合的函数,文中说假设拟合残差图更容易优化,也就是说:F(x) := H(x)-x比F(x) := H(x)更容易优化,接下来举了一个例子,极端情况下:desired underlying mapping要拟合的是identity mapping，这时候残差网络的任务就是拟合F(x): 0,而原本的plain结构的话就是F(x) : x,而F(x): 0任务会更容易,原因是:resnet（残差网络）的F（x）究竟长什么样子？中theone的答案:

F是求和前网络映射，H是从输入到求和后的网络映射。比如把5映射到5.1，那么引入残差前是F'(5)=5.1，引入残差后是H(5)=5.1, H(5)=F(5)+5, F(5)=0.1。这里的F'和F都表示网络参数映射，引入残差后的映射对输出的变化更敏感。比如s输出从5.1变到5.2，映射F'的输出增加了1/51=2%，而对于残差结构输出从5.1到5.2，映射F是从0.1到0.2，增加了100%。明显后者输出变化对权重的调整作用更大，所以效果更好。残差的思想都是去掉相同的主体部分，从而突出微小的变化，看到残差网络我第一反应就是差分放大器

后续的实验也是证明了假设的, 残差网络比plain网络更好训练。因此，ResNet解决的是更好地训练网络的问题，王峰的答案算是对ResNet之所以好的一个理论论证吧.

作者：薰风初入弦
https://www.zhihu.com/question/64494691/answer/786270699

看了这个问题之后我思考了很久，于是写出了这篇专栏，现在贴过来当答案。

首先是跟着论文的思路走，了解作者提出resnet的“心路历程”，最后也有些个人整理的理解。

ps：欢迎关注我的专栏，这段时间我会持续更新，并且在更完约莫十几篇论文阅读后，会再写一些模型实现/代码方面的理解。

https://zhuanlan.zhihu.com/IsonomiaCS

一、引言：为什么会有ResNet？Why ResNet？

神经网络叠的越深，则学习出的效果就一定会越好吗？

答案无疑是否定的，人们发现当模型层数增加到某种程度，模型的效果将会不升反降。也就是说，深度模型发生了退化（degradation）情况。

那么，为什么会出现这种情况？

1. 过拟合？Overfitting？

首先印入脑海的就是Andrew Ng机器学习公开课[1]的过拟合问题

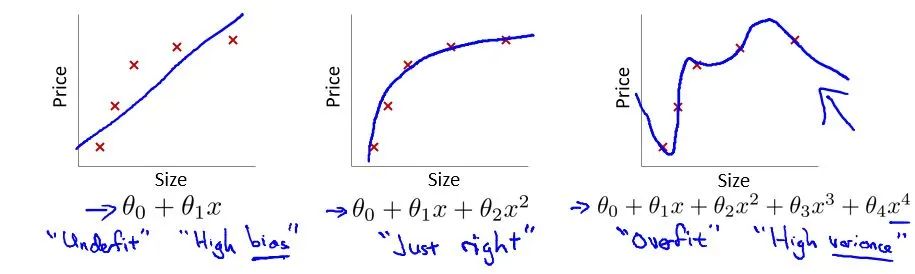
在这个多项式回归问题中，左边的模型是欠拟合（under fit）的此时有很高的偏差（high bias），中间的拟合比较成功，而右边则是典型的过拟合（overfit），此时由于模型过于复杂，导致了高方差（high variance）。

然而，很明显当前CNN面临的效果退化不是因为过拟合，因为过拟合的现象是"高方差，低偏差"，即测试误差大而训练误差小。但实际上，深层CNN的训练误差和测试误差都很大。

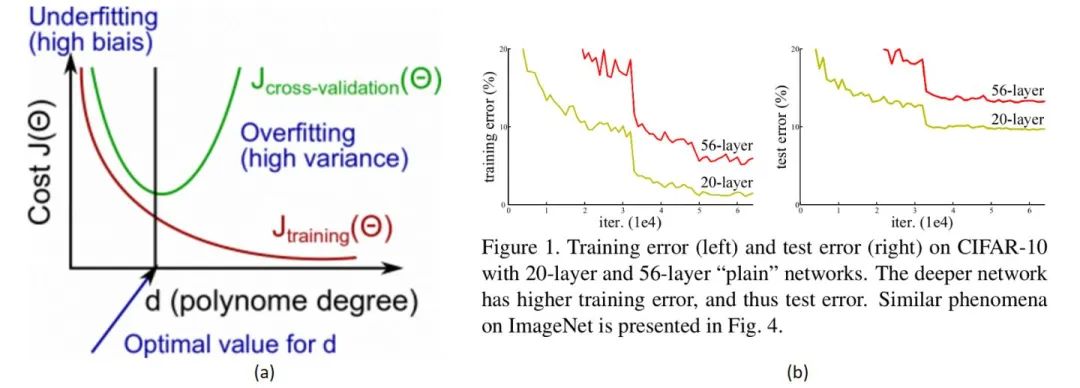
2. 梯度爆炸/消失？Gradient Exploding/Vanishing？

除此之外，最受人认可的原因就是“梯度爆炸/消失（弥散）”了。为了理解什么是梯度弥散，首先回顾一下反向传播的知识。

假设我们现在需要计算一个函数， , ,在时的梯度，那么首先可以做出如下所示的计算图。

将 , ,带入，其中，令 ,一步步计算，很容易就能得出。

这就是前向传播（计算图上部分绿色打印字体与蓝色手写字体），即：

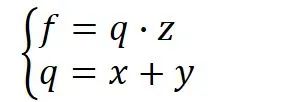
前向传播是从输入一步步向前计算输出，而反向传播则是从输出反向一点点推出输入的梯度(计算图下红色的部分)。

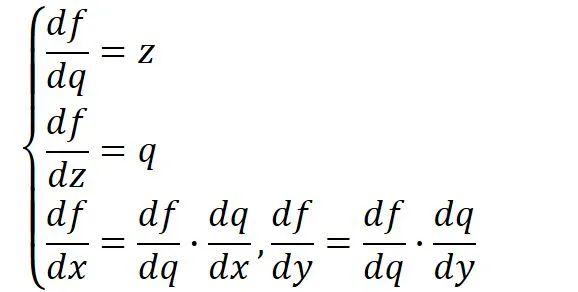
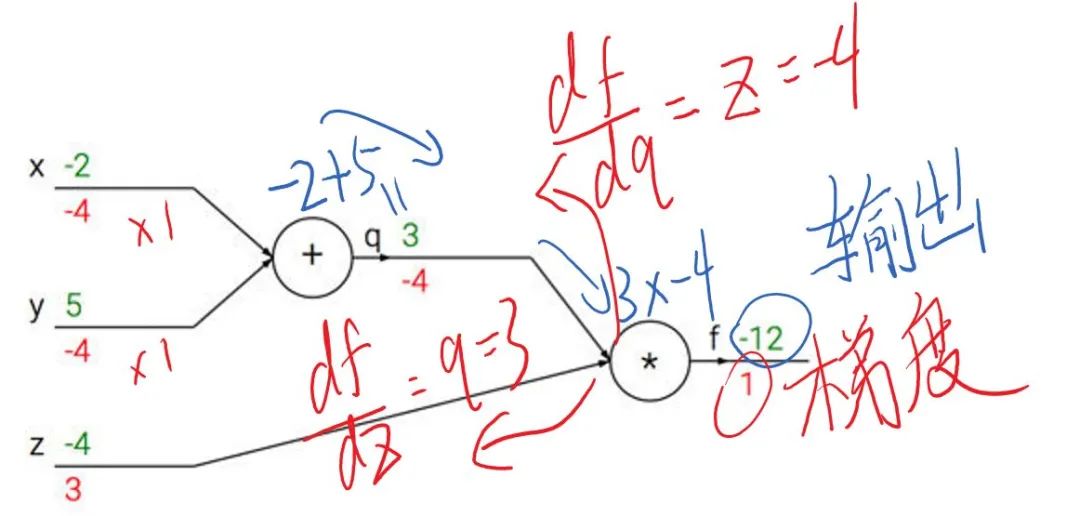
注：这里的反向传播假设输出端接受之前回传的梯度为1（也可以是输出对输出求导=1）

观察上述反向传播，不难发现，在输出端梯度的模值，经过回传扩大了3~4倍。

这是由于反向传播结果的数值大小不止取决于求导的式子，很大程度上也取决于输入的模值。当计算图每次输入的模值都大于1，那么经过很多层回传，梯度将不可避免地呈几何倍数增长（每次都变成3~4倍，重复上万次，想象一下310000有多大……），直到Nan。这就是梯度爆炸现象。

当然反过来，如果我们每个阶段输入的模恒小于1，那么梯度也将不可避免地呈几何倍数下降（比如每次都变成原来的三分之一，重复一万次就是3-10000），直到0。这就是梯度消失现象。值得一提的是，由于人为的参数设置，梯度更倾向于消失而不是爆炸。

由于至今神经网络都以反向传播为参数更新的基础，所以梯度消失问题听起来很有道理。然而，事实也并非如此，至少不止如此。

我们现在无论用Pytorch还是Tensorflow，都会自然而然地加上Bacth Normalization(简称BN)，而BN的作用本质上也是控制每层输入的模值，因此梯度的爆炸/消失现象理应在很早就被解决了（至少解决了大半）。

不是过拟合，也不是梯度消失，这就很尴尬了……CNN没有遇到我们熟知的两个老大难问题，却还是随着模型的加深而导致效果退化。无需任何数学论证，我们都会觉得这不符合常理。等等，不符合常理……

3. 为什么模型退化不符合常理？

按理说，当我们堆叠一个模型时，理所当然的会认为效果会越堆越好。因为，假设一个比较浅的网络已经可以达到不错的效果，那么即使之后堆上去的网络什么也不做，模型的效果也不会变差。

然而事实上，这却是问题所在。“什么都不做”恰好是当前神经网络最难做到的东西之一。

MobileNet V2的论文[2]也提到过类似的现象，由于非线性激活函数Relu的存在，每次输入到输出的过程都几乎是不可逆的（信息损失）。我们很难从输出反推回完整的输入。

也许赋予神经网络无限可能性的“非线性”让神经网络模型走得太远，却也让它忘记了为什么出发（想想还挺哲学）。这也使得特征随着层层前向传播得到完整保留（什么也不做）的可能性都微乎其微。

用学术点的话说，这种神经网络丢失的“不忘初心”/“什么都不做”的品质叫做恒等映射（identity mapping）。

因此，可以认为Residual Learning的初衷，其实是让模型的内部结构至少有恒等映射的能力。以保证在堆叠网络的过程中，网络至少不会因为继续堆叠而产生退化！

二、深度残差学习 Deep Residual Learning

1. 残差学习 Residual Learning

前面分析得出，如果深层网络后面的层都是是恒等映射，那么模型就可以转化为一个浅层网络。那现在的问题就是如何得到恒等映射了。

事实上，已有的神经网络很难拟合潜在的恒等映射函数H(x) = x。

但如果把网络设计为H(x) = F(x) + x，即直接把恒等映射作为网络的一部分。就可以把问题转化为学习一个残差函数F(x) = H(x) - x.

只要F(x)=0，就构成了一个恒等映射H(x) = x。而且，拟合残差至少比拟合恒等映射容易得多。

于是，就有了论文[3]中的Residual block结构

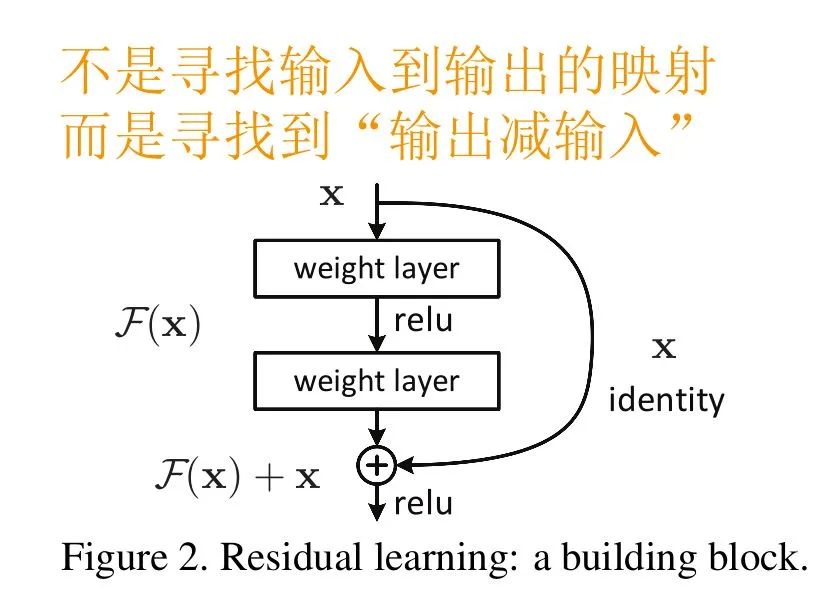
图中右侧的曲线叫做跳接（shortcut connection），通过跳接在激活函数前，将上一层（或几层）之前的输出与本层计算的输出相加，将求和的结果输入到激活函数中做为本层的输出。

用数学语言描述，假设Residual Block的输入为，则输出等于：

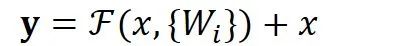
其中是我们学习的目标，即输出输入的残差。以上图为例，残差部分是中间有一个Relu激活的双层权重，即：

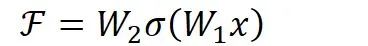
其中指代Relu，而指代两层权重。

顺带一提，这里一个Block中必须至少含有两个层，否则就会出现很滑稽的情况：

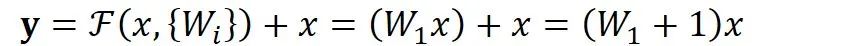
显然这样加了和没加差不多……

2.网络结构与维度问题

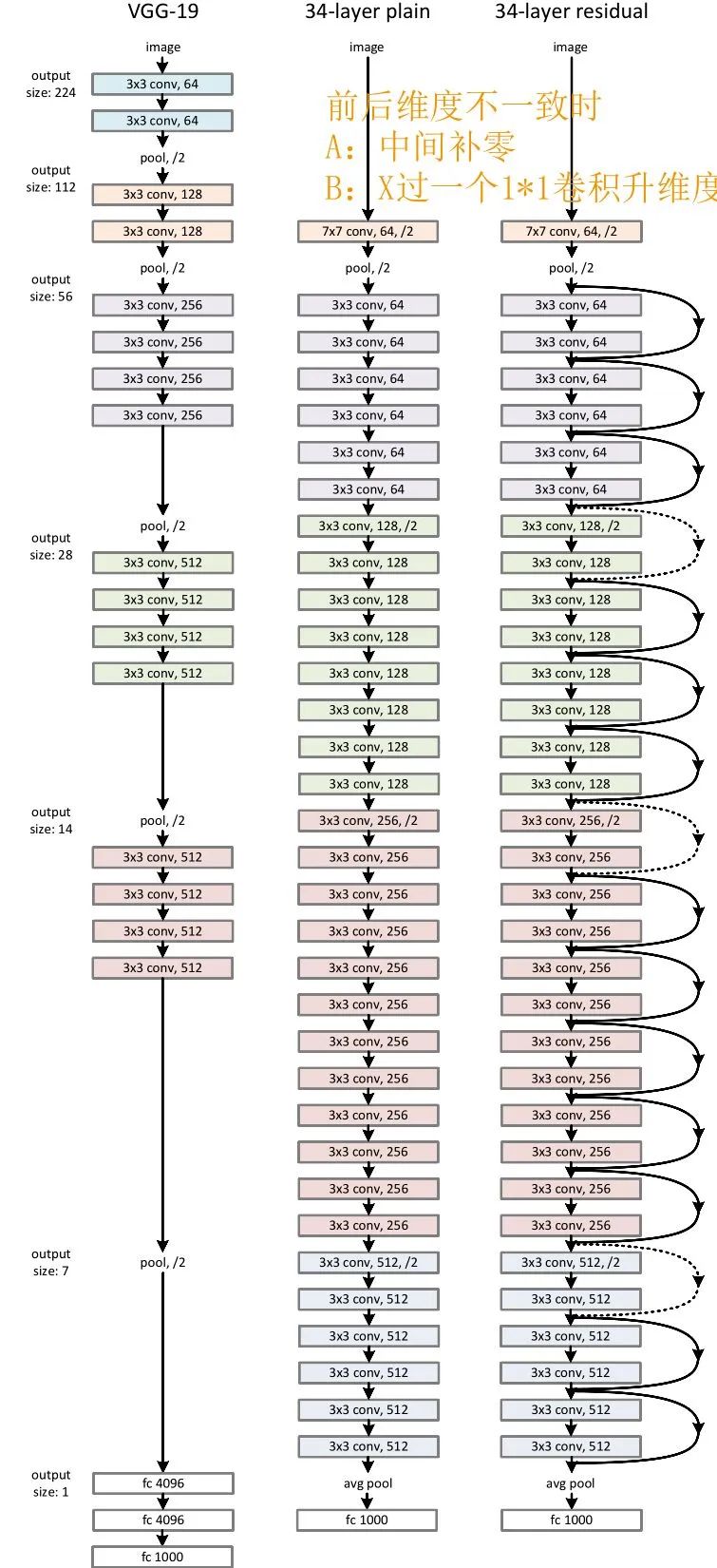
ResNet结构示意图（左到右分别是VGG，没有残差的PlainNet，有残差的ResNet）

论文中原始的ResNet34与VGG的结构如上图所示，可以看到即使是当年号称“Very Deep”的VGG，和最基础的Resnet在深度上相比都是个弟弟。

可能有好奇心宝宝发现了，跳接的曲线中大部分是实现，但也有少部分虚线。这些虚线的代表这些Block前后的维度不一致，因为去掉残差结构的Plain网络还是参照了VGG经典的设计思路：每隔x层，空间上/2（下采样）但深度翻倍。

也就是说，维度不一致体现在两个层面：

空间上不一致
深度上不一致

空间上不一致很简单，只需要在跳接的部分给输入x加上一个线性映射 ,即：

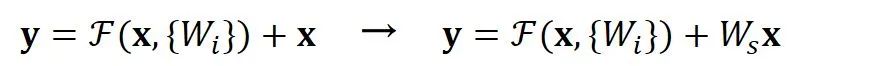
而对于深度上的不一致，则有两种解决办法，一种是在跳接过程中加一个1*1的卷积层进行升维，另一种则是直接简单粗暴地补零。事实证明两种方法都行得通。

注：深度上和空间上维度的不一致是分开处理的，但很多人将两者混为一谈（包括目前某乎一些高赞文章），这导致了一些人在模型的实现上感到困惑（比如当年的我）。

3. torchvision中的官方实现

事实上论文中的ResNet并不是最常用的，我们可以在Torchvision的模型库中找到一些很不错的例子，这里拿Resnet18为例：

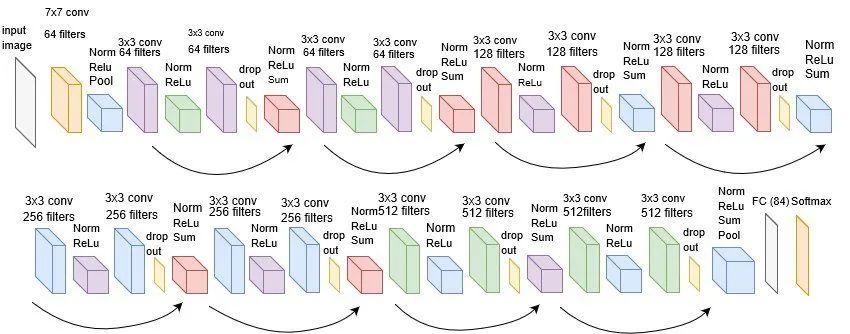
运行代码：

import torchvisionmodel = torchvision.models.resnet18(pretrained=False) #我们不下载预训练权重print(model)

得到输出：

ResNet(  (conv1): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)  (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)  (relu): ReLU(inplace)  (maxpool): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)  (layer1): Sequential(    (0): BasicBlock(      (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)      (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)      (relu): ReLU(inplace)      (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)      (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)    )    (1): BasicBlock(      (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)      (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)      (relu): ReLU(inplace)      (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)      (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)    )  )  (layer2): Sequential(    (0): BasicBlock(      (conv1): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)      (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)      (relu): ReLU(inplace)      (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)      (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)      (downsample): Sequential(        (0): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)        (1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)      )    )    (1): BasicBlock(      (conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)      (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)      (relu): ReLU(inplace)      (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)      (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)    )  )  (layer3): Sequential(    (0): BasicBlock(      (conv1): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)      (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)      (relu): ReLU(inplace)      (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)      (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)      (downsample): Sequential(        (0): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2), bias=False)        (1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)      )    )    (1): BasicBlock(      (conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)      (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)      (relu): ReLU(inplace)      (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)      (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)    )  )  (layer4): Sequential(    (0): BasicBlock(      (conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)      (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)      (relu): ReLU(inplace)      (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)      (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)      (downsample): Sequential(        (0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)        (1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)      )    )    (1): BasicBlock(      (conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)      (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)      (relu): ReLU(inplace)      (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)      (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)    )  )  (avgpool): AvgPool2d(kernel_size=7, stride=1, padding=0)  (fc): Linear(in_features=512, out_features=1000, bias=True))

薰风说 Thinkings

上述的内容是我以自己的角度思考作者提出ResNet的心路历程，我比作者蔡很多，所以难免出现思考不全的地方。

ResNet是如此简洁高效，以至于模型提出后还有无数论文讨论“ResNet到底解决了什么问题(The Shattered Gradients Problem: If resnets are the answer, then what is the question?)”[4]

论文[4]认为，即使BN过后梯度的模稳定在了正常范围内，但梯度的相关性实际上是随着层数增加持续衰减的。而经过证明，ResNet可以有效减少这种相关性的衰减。

对于层的网络来说，没有残差表示的Plain Net梯度相关性的衰减在，而ResNet的衰减却只有。这也验证了ResNet论文本身的观点，网络训练难度随着层数增长的速度不是线性，而至少是多项式等级的增长（如果该论文属实，则可能是指数级增长的）

而对于“梯度弥散”观点来说，在输出引入一个输入x的恒等映射，则梯度也会对应地引入一个常数1，这样的网络的确不容易出现梯度值异常，在某种意义上，起到了稳定梯度的作用。

除此之外，shortcut类似的方法也并不是第一次提出，之前就有“Highway Networks”。可以只管理解为，以往参数要得到梯度，需要快递员将梯度一层一层中转到参数手中（就像我取个快递，都显示要从“上海市”发往“闵行分拣中心”，闵大荒日常被踢出上海籍）。而跳接实际上给梯度开了一条“高速公路”（取快递可以直接用无人机空投到我手里了），效率自然大幅提高，不过这只是个比较想当然的理由。

上面的理解很多论文都讲过，但我个人最喜欢下面两个理解。

第一个已经由Feature Pyramid Network[5]提出了，那就是跳连接相加可以实现不同分辨率特征的组合，因为浅层容易有高分辨率但是低级语义的特征，而深层的特征有高级语义，但分辨率就很低了。

第二个理解则是说，引入跳接实际上让模型自身有了更加“灵活”的结构，即在训练过程本身，模型可以选择在每一个部分是“更多进行卷积与非线性变换”还是“更多倾向于什么都不做”，抑或是将两者结合。模型在训练便可以自适应本身的结构，这听起来是多么酷的一件事啊！

有的人也许会纳闷，我们已经知道一个模型的来龙去脉了，那么在一个客观上已经十分优秀的模型，强加那么多主观的个人判断有意思吗？

然而笔者还是相信，更多角度的思考有助于我们发现现有模型的不足，以及值得改进的点。比如我最喜欢的两个理解就可以引申出这样的问题“虽然跳接可以结合不同分辨率，但ResNet显然没有充分利用这个优点，因为每个shortcut顶多跨越一种分辨率（大部分还不会发生跨越）”。

那么“如果用跳接组合更多分辨率的特征，模型的效果会不会更好？”这就是DenseNet回答我们的问题了。

参考文献

[1]https://www.coursera.org/learn/machine-learning
[2]Sandler M, Howard A, Zhu M, et al. MobileNetV2: Inverted Residuals and Linear Bottlenecks[J]. 2018.

[3]He K, Zhang X, Ren S, et al. Deep Residual Learning for Image Recognition[J]. 2015.

[4]Balduzzi D , Frean M , Leary L , et al. The Shattered Gradients Problem: If resnets are the answer, then what is the question?[J]. 2017.

[5]Lin T Y , Dollár, Piotr, Girshick R , et al. Feature Pyramid Networks for Object Detection[J]. 2016.

投稿或交流学习，备注： 昵称-学校（公司）-方向，进入DL&NLP交流群。

方向有很多：机器学习、深度学习，python，情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。