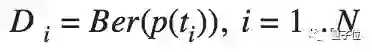TensorFlow手把手教你概率编程：TF Probability内置了开源教材，新手友好

晓查 栗子 发自 凹非寺 
量子位 出品 | 公众号 QbitAI

大家可能知道，要做概率编程 (Probabilistic Programming) 的话，TensorFlow Probability (TFP) 这个库是个不错的选择。

大家可能不知道，现在TFP里面有了一本开源教材，可以手把手教你学概率编程。就算是新手，就算没有用过TFP，也不要紧：

就是这本书，Bayesian Methods for Hackers。入门教材，注重实践，拥有各种示例。

(TFP版本的教材，也是先前PyMC3版本的一个补充。)

这本教材，除了适合新人上手概率编程，也展示了概率编程在现实问题中的应用。

概率编程，人人可学

贝叶斯方法，提供了一个相对直观的框架，把信念表征 (Representing Beliefs) 出来，再根据新的数据来更新这些信念。

教材以TFP库为根基，向大家传授这样的技术，还有许多动手实践帮助大家练习。

这本书是在Google Colab里面写的，里面的Python示例可以运行也可以修改。

现在有友好的教材了，来学概率编程吧。毕竟，从金融到石油天然气，各行各业可能都用得到：不确定性 (Uncertainty) 无处不在，许多事件都可能受到外部因素的影响。如果抛开这些因素，模型就可能不准了，所以才有了概率编程，才有了TFP库。

那么，来看一下TFP是怎样解决现实问题的：

解决现实世界的问题

Bayesian Methods for Hackers一书从简单问题开始，比如用于硬币正反和骰子点数问题，然后转向更为现实的问题，包括从理解宇宙到检测在线用户行为的变化。

下面我们将概述一个著名的现实世界问题：1986年挑战者航天飞机灾难性事故。书中对此问题有更详细的处理。

1986年1月28日，美国挑战者号航天飞机的第25次飞行中，由于O形圈故障，挑战者号的两个固体火箭助推器中的一个爆炸了。 虽然工程师与O形圈制造商就先前飞行中的损坏进行了多次沟通，但制造商认为风险是可以接受的。

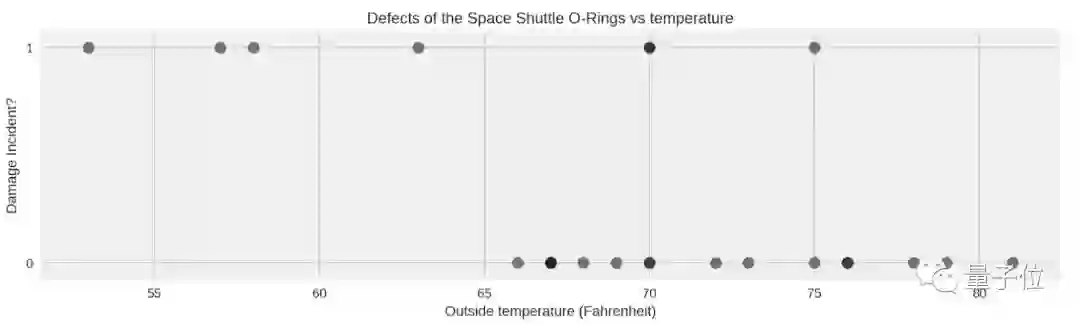
下图描述了对先前航天飞机任务中的七次O形圈损坏事件的观测，这是损坏事件对环境温度的函数。 （在70度时，有两个损坏事件。注：温度均为华氏度，下同。）

你会注意到，随着温度的降低，O形圈损坏的比例会显著增加，但是没有明显的温度阈值，低于该阈值时O形圈就一定会失效。 与现实世界大多数现象一样，这个问题存在不确定性。 我们希望在给定温度t下，确定O形圈失效的概率是多少？

我们可以使用逻辑函数模拟温度t下O形环损坏的概率p ：

其中β确定概率函数的形状，α是偏移项，控制函数的左右移动。 由于这两个参数都可以是正的或负的，没有特定的边界或大小的偏差，我们可以将它们建模为高斯分布随机变量：

在TFP中，我们可以用tfp.distributions.Normal直观地表示α和β，代码如下：

请注意，我们在第8行得到p(t)的实际值0或1，其中我们使用先前在第6行和第7行中采样的α和β值对概率函数进行采样。另外，请注意evaluate()辅助函数允许我们无缝地在图形和eager模式之间转换，同时将张量值转换为numpy。

为了将温度t、失效概率p(t)与我们的观测数据联系起来，我们可以使用带参数p(t)的伯努利随机变量。 注意，通常，Ber(p)是随机变量，其值为1的概率为p，其余情况下为0。 因此，生成模型的最后一部分是某温度下观测到有缺陷事件的数量D𝑖 ，它可以建模为：

鉴于这种生成模型，我们希望找到模型参数，可以解释观察到的数据，这正是是概率推理的目标。

TFP通过使用非标准化联合对数概率函数评估模型来执行概率推断。此joint_log_prob的参数是数据和模型状态。 该函数返回参数化模型生成观测数据的联合概率的对数。

接下来，我们使用joint_log_prob函数，并将其发送到tfp.mcmc模块。 马尔可夫链蒙特卡洛（MCMC）算法对未知输入值进行有根据的猜测，计算joint_log_prob函数中参数集的可能性。 通过多次重复此过程，MCMC构建了可能参数的分布。 构建此分布是概率推理的目标。

因此，我们将通过challenge_joint_log_prob函数设置一种特定类型的MCMC，称为“哈密顿蒙特卡洛”：

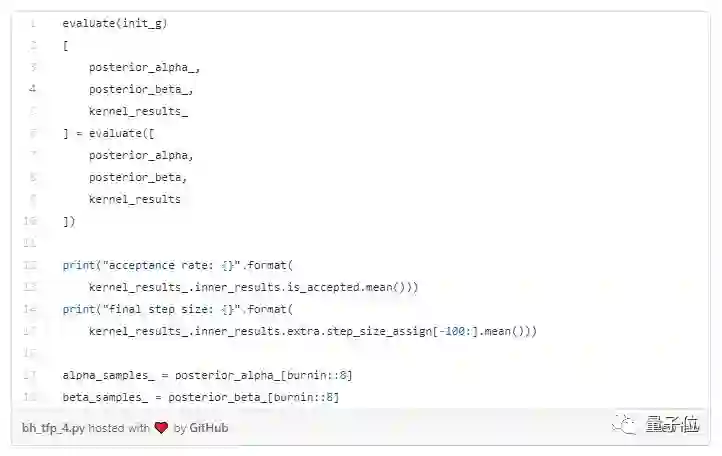
最后，我们将通过evaluate()辅助函数进行推理：

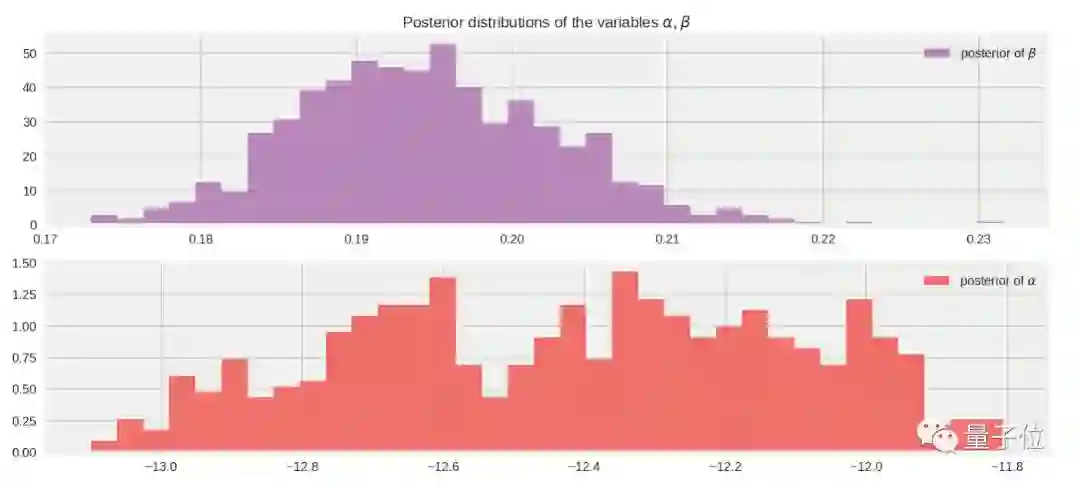
通过绘制α和β的分布图，我们注意到这两个参数分布相当宽：

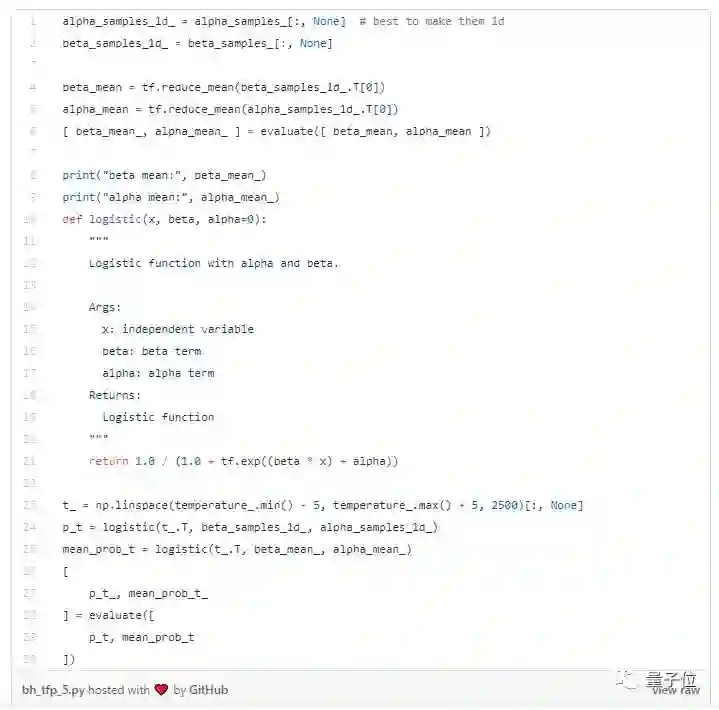
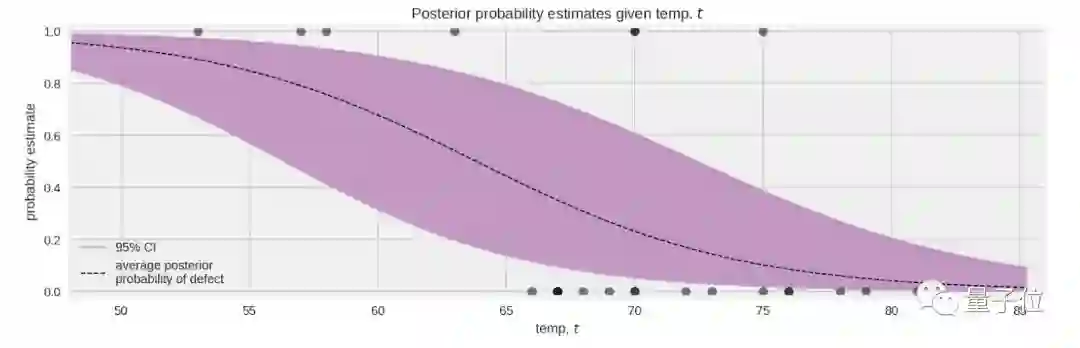
正如我们上面提到的，我们真正想知道的是： 在给定温度下O形环损坏的预期概率是多少？ 为了计算这个概率，我们可以对来自后验的所有样本求平均值，得到概率的可能值。

然后我们可以在整个温度范围内计算95％的可信区间。 请注意，这是一个可靠的区间，而不是通常在统计分析方法中的置信区间。 95％可信区间告诉我们，我们可以95％的概率确定真实值将位于此区间内。 例如，正如下图中的紫色区域，在50度时，我们可以95％确定O形圈损坏的概率介于1.0和0.80之间。

挑战者号事故发生当天的温度为31华氏度。事实证明，O形圈失效的后验分布将使我们高度确信会出现损坏的问题。

这种相当简单的概率分析证明了TFP和贝叶斯方法的强大功能：它们可以提供有价值的分析，对可能产生重大后果的实际问题进行预测。

关于TensorFlow Probability

TensorFlow Probability是一个Python库，可以把概率模型和深度学习轻松结合起来。

机器学习研究人员或者工程师，都可以用它编码领域知识 (Domain Knowledge)，就是某个特定领域的专业知识，从而理解数据并写出自己的应用。这里有：

· 许多种类的概率分布，以及Bijectors；

· 搭建概率模型的各种工具，比如概率层 (Probabilistic Layers) 以及Edward2语言；

· 变分推理 (Variational Inference) 和马尔科夫链蒙特卡洛 (MCMC) ；

· 以及各种优化器，比如Nelder-Mead，BFGS和SGLD。

现在，连教材也有了，大家可以开始愉快地学习了。

TensorFlow Probability传送门：
https://www.tensorflow.org/probability/

《Bayesian Methods for Hackers》电子书：

https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers

博客传送门：
https://medium.com/tensorflow/an-introduction-to-probabilistic-programming-now-available-in-tensorflow-probability-6dcc003ca29e?linkId=60908456