不使用残差连接，ICML新研究靠初始化训练上万层标准CNN

2018 年 6 月 18 日 机器之心

选自arXiv

机器之心编译

参与：路、思源

本论文介绍了如何利用动态等距和平均场理论完成一万层原版卷积神经网络的训练，研究者证明了仅仅使用恰当的初始化机制就能有效训练一万层原版 CNN 甚至更多层。研究者通过信号传播的平均场等理论导出该初始化机制，并表明在关键线上初始化的网络信号能高效传播，因此即使不使用残差连接或密集型连接等方式，超深卷积网络也能有效地训练。

1. 引言

深度卷积神经网络（CNN）是深度学习成功的关键。基于 CNN 的架构在计算机视觉、语音识别、自然语言处理以及最近的围棋博弈等多个领域取得了前所未有的准确率。

随着深度卷积网络的深度增加，其性能也得到了改善。例如，一些在 ImageNet (Deng et al., 2009) 上表现最好的模型使用了数百甚至上千层卷积网络（He et al., 2016a;b）。但是这些非常深的网络架构只有在使用残差连接（He et al., 2016a）和批归一化（Ioffe & Szegedy, 2015）等技术时才能有效训练。这些技术是否能够从本质上提升模型性能或它们是否是训练超深度网络的必要手段，这个问题仍然有待解决。在本论文中，研究者结合理论和实验来研究原版 CNN，以理清可训练性和泛化性能的问题。研究者证明，审慎、以理论为基础的初始化机制可以在不使用其他架构技巧的情况下训练 10000 层原版 CNN。

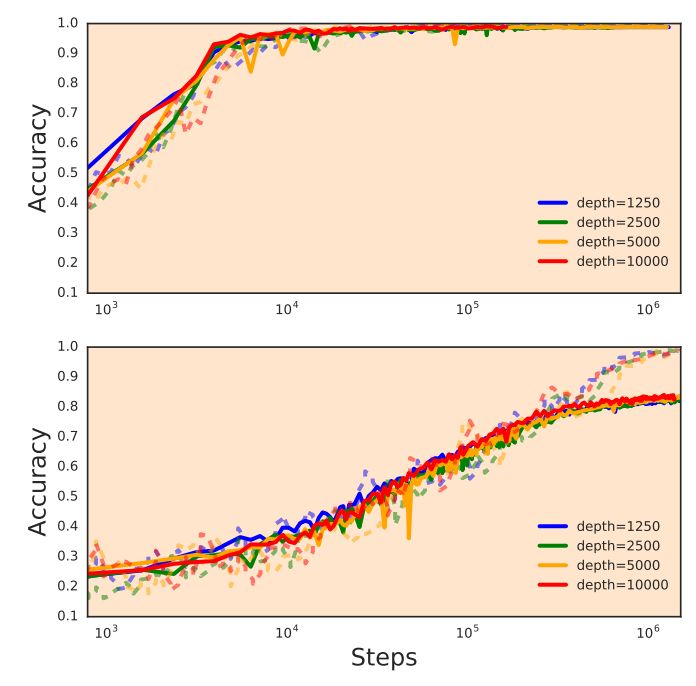
图 1. 在不使用批归一化或残差连接而仅使用 Delta-Orthogonal 初始化（具备关键权重、偏差方差和恰当的非线性函数）的情况下，非常深的 CNN 网络架构是可以训练的。图为在 MNIST（上）和 CIFAR- 10（下）上模型深度为 1,250、2,500、5,000 和 10, 000 时的测试曲线（实线）和训练曲线（虚线）。

近期有研究使用平均场理论（mean field theory）来构建对使用随机参数的神经网络的理论理解（Poole et al., 2016; Schoenholz et al., 2017; Yang & Schoenholz, 2017; Schoenholz et al., 2017; Karakida et al., 2018; Hayou et al., 2018; Hanin & Rolnick, 2018; Yang & Schoenholz, 2018）。这些研究通过探索哪些信号可以在初始化阶段传播来揭示网络的最大深度，并通过实验验证：当信号可以遍历网络时，网络可得到准确训练。在全连接层中，该理论还预测初始化超参数空间中存在从有序到混乱阶段的转变（相变/phase transition）。对于在阶段分割的关键线上进行初始化的网络，如果信号可以传播，那么任意深度的网络都可以被训练。

但尽管平均场理论能够捕捉到随机神经网络的「平均」动态，但它无法量化对于梯度下降稳定性至关重要的梯度波动。相关研究（Saxe et al., 2013; Pennington et al., 2017; 2018）使用输入-输出雅可比矩阵和随机矩阵理论，从激活函数和获取初始随机权重矩阵的分布的角度来量化奇异值分布。这些研究认为当雅可比矩阵是良态的（well-conditioned）时网络可以得到最高效的训练，条件是使用正交权重矩阵而非高斯权重矩阵。这些方法允许研究者高效训练非常深的网络架构，但是目前为止它们仅限于由全连接层组成的神经网络。

本论文继续该研究方向，并将其扩展至卷积网络。研究者展示了一个定义明确且适用于卷积网络的平均场理论，即使图像较小，它也限制于信道数较多的情况。此外，卷积网络具备和全连接网络一样的从有序到混乱的相变，有序相位出现梯度消失，混乱相位出现梯度爆炸。和全连接层一样，在分割两种相位的关键线上进行初始化的超深 CNN 可以相对容易地进行训练。

现在来看平均场理论，研究者将（Pennington et al., 2017; 2018）的随机矩阵分析扩展至卷积环境中。此外，研究者还从小波变换文献中发现了一种高效的构建方法：使用块循环结构（对应卷积算子）生成随机正交矩阵。该构建促进了卷积层的随机正交初始化，并为任意深度网络的端到端雅可比矩阵设置了较好的条件数。实验证明使用该初始化的网络训练速度显著快于标准卷积网络。

最后，研究者强调即使全连接网络和卷积网络的从有序到混乱相位界限看似一样，但底层的平均场理论实际上有很大不同。具体来说，卷积理论的新颖之处在于存在多个深度来控制不同空间频率处的信号传播。在深度极限较大的情况下，信号只能沿着最小空间结构模式进行传播；所有其他模式即使是在关键线上最终也都会退化。研究者假设这种信号退化对泛化性能有害，并开发出一个修正版的初始化机制，该机制允许信号在所有频率中均衡传播。研究者将该机制称为 Delta-Orthogonal 初始化，其正交核从空间非均匀分布中得出，允许训练 10000 层甚至更多层原版 CNN，同时不会造成性能下降。

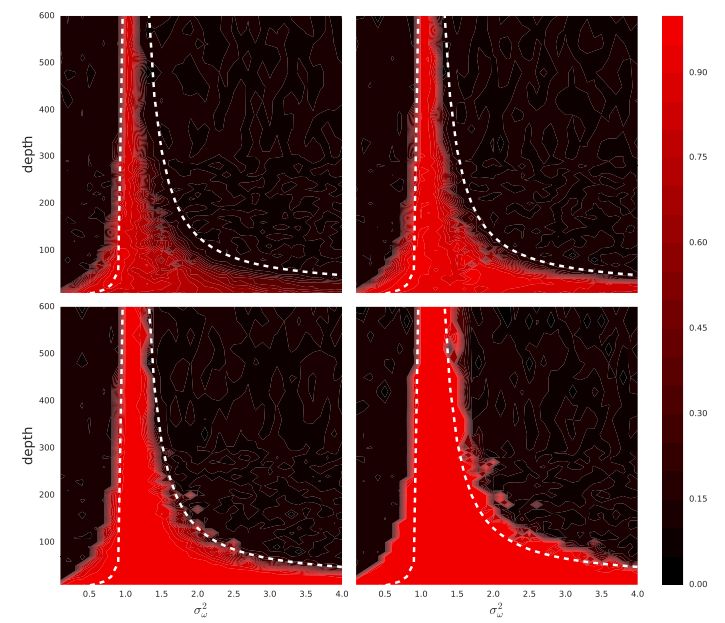
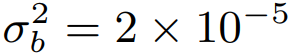
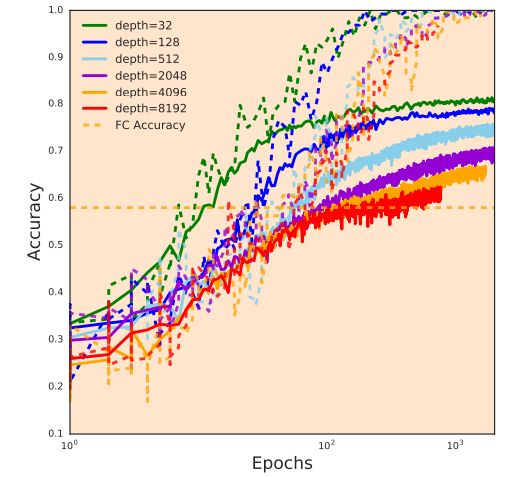
图 2. 平均场理论预测 CNN 的最大可训练深度。对于偏置项的固定方差，此热图显示在 MNIST 数据集上，深度为 L 和权重方差 σ_w 的网络在 (a) 500、(b) 2,500、(c) 10,000 以及 (d) 100,000 个训练步之后的训练准确率。白色虚线是多个典型 (6ξ_c) 深度下控制收敛至不动点的线。

图 3. 在 CIFAR-10 上，使用正交核进行不同深度初始化的 CNN 的测试曲线（实线）和训练曲线（虚线）。这些曲线（除了早停的 8192）的训练准确率都达到了 100%，而泛化性能随着深度增加逐渐下降，很可能是因为空间非均匀模式的衰减。图 1 的 Delta-Orthogonal 初始化解决了这一性能下降问题。

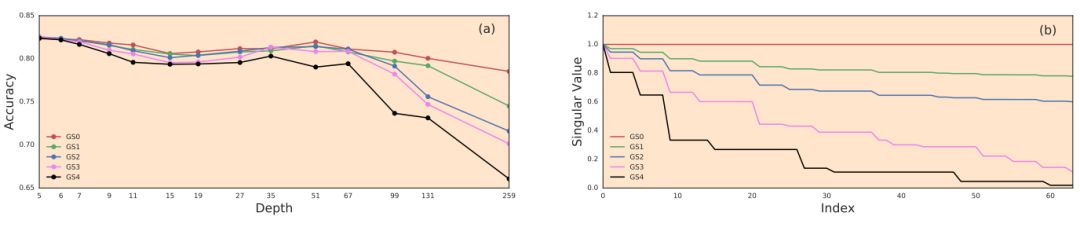
图 4. 随深度变化的测试性能与广义平均算子（A_v*）的奇异值分布（SVD）相关。（a）在关键线上的初始化，研究者检查了使用不同深度和不同非均匀方差向量的高斯初始化的 CNN 的测试准确率。研究者将来自 delta 函数（红色）的方差向量改变为均匀分布的方差向量（黑色）。从深度为 35 开始，测试准确率曲线也从红色变成了黑色。（b）所选方差向量的（A_v*）SVD。x 轴表示奇异值的索引，每个方差向量共有 64 个奇异值（每个有 64 个副本）。

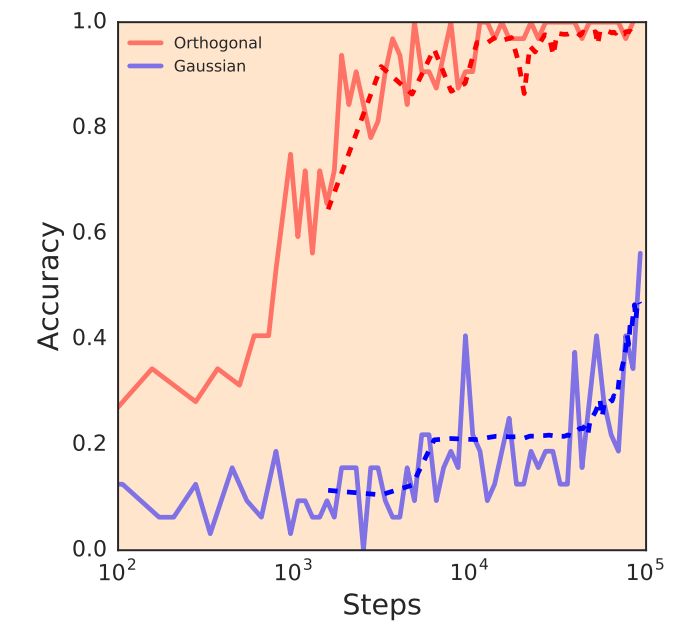
图 5. 正交初始化带来 CNN 的更快速训练。使用具备同样权重方差的正交初始化（红色）和高斯初始化（黑色）对 4000 层 CNN 进行训练，实线为训练曲线，虚线为测试曲线。

3. 实验

研究者以 tanh 作为激活函数，在 MNIST 和 CIFAR-10 上训练了一个非常深的 CNN。研究者使用以下原版 CNN 架构。首先使用 3 个步幅分别为 1、2、2 的 3 × 3 × c 卷积，以将信道数量增加到 c，将空间维度减少到 7 × 7（对于 CIFAR-10 是 8 × 8），然后使用 d 个 3 × 3 × c 卷积，d 的范围是 [2, 10,000]。最后，使用一个平均池化层和全连接层。这里当 d ≤ 256 时 c = 256，当 d 大于 256 时 c = 128。为了最大程度地支持本文提出的理论，研究者不使用任何常见技术（包括学习率衰减）。注意，从计算角度来看，早期的下采样是必需的，但是它会降低最大性能上限；如使用下采样在 CIFAR-10 上获取的最优测试准确率是 82%。研究者额外进行了一个实验，在不使用下采样的情况下训练一个 50 层的网络，得到了 89.9% 的测试准确率，与使用 tanh 架构在 CIFAR-10 上得到的最优准确率不相上下（89.82%）。

论文：Dynamical Isometry and a Mean Field Theory of CNNs: How to Train 10,000-Layer Vanilla Convolutional Neural Networks

论文链接：https://arxiv.org/abs/1806.05393

摘要：近年来，计算机视觉领域的顶级方法越来越多地使用深度卷积神经网络（CNN），其中最成功的一些模型甚至采用了数千层网络。而梯度消失、梯度爆炸这类问题使得训练这样的深层网络成为挑战。虽然残差连接和批归一化能够完成这种深度的模型训练，但此类专用架构设计对训练深度 CNN 是否真的必需还不清楚。在此研究中，我们证明了仅仅使用恰当的初始化机制就能够训练一万层原版 CNN 甚至更多层。我们通过信号传播的平均场（mean field）理论，以及定义动态等距（dynamical isometry）、输入-输出雅可比矩阵的奇异值平衡的条件，从理论上导出该初始化机制。这些条件要求卷积算子是正交变换，以保留范数。我们展示了生成此类随机初始化正交卷积核的算法，实验证明这可以促进非常深的网络架构的高效训练。