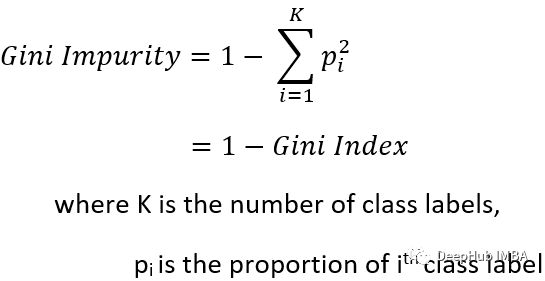数据科学中的 10 个重要概念和图表的含义

大数据文摘转载自数据派THU

来源：DeepHub IMBA

“当算法给你一条曲线时，一定要知道这个曲线的含义！”

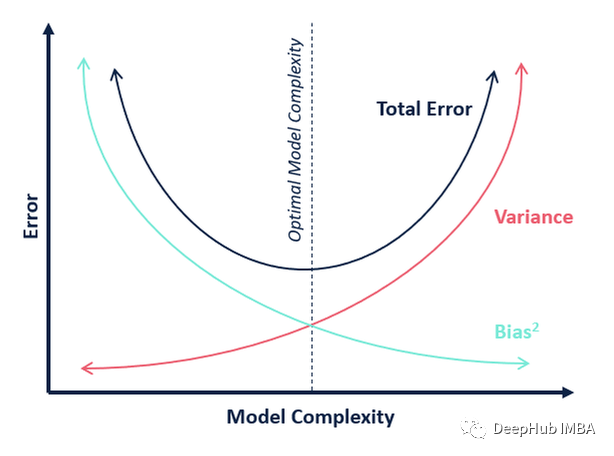
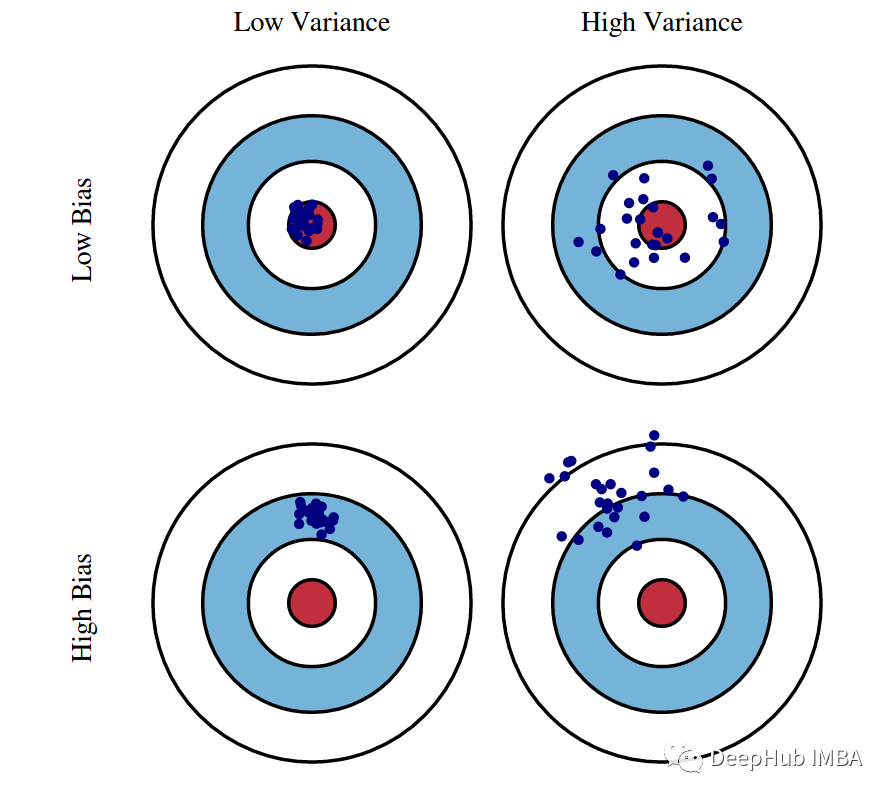
1、偏差-方差权衡

这是一个总是在机器学习最重要理论中名列前茅的概念。机器学习中的几乎所有算法（包括深度学习）都努力在偏差和方差之间取得适当的平衡，这个图清楚地解释了二者的对立关系。

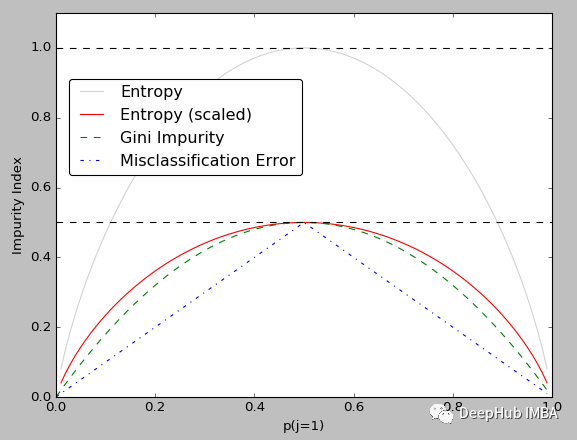
2、基尼不纯度与熵

Gini（缺乏同质性的度量）和 Entropy（随机性的度量）都是决策树中节点不纯度的度量。

对于这两个概念更重要的是要了解它们之间的关系，以便能够在给定的场景中选择正确的指标。

基尼不纯度（系数）通常比熵更容易计算（因为熵涉及对数计算）

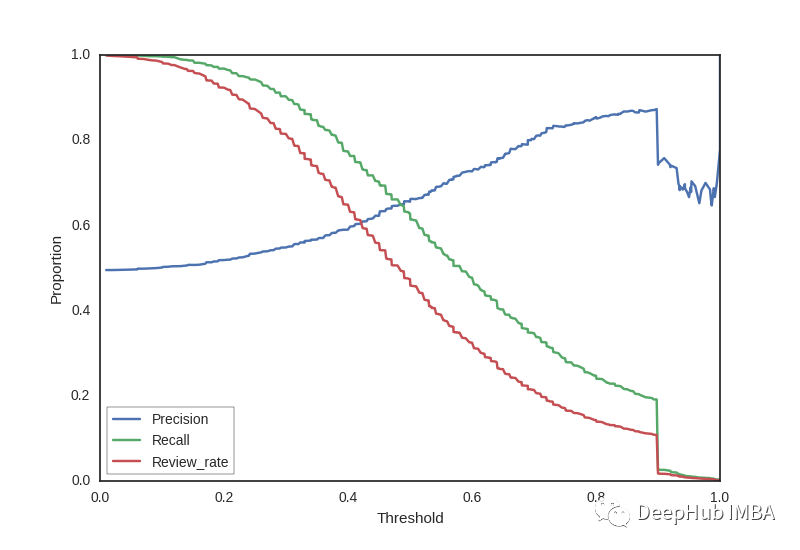
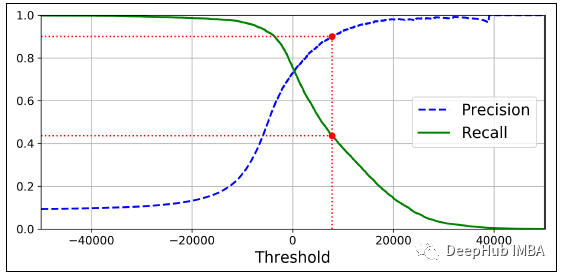
3、精度与召回曲线

精度-召回曲线显示了不同阈值的精度和召回率之间的权衡。曲线下面积大代表高召回率和高精度，其中高精度与低误报率相关，高召回率与低误报率相关。

它可以帮助我们根据需要选择正确的阈值。例如，如果我们的目标是减少类型 1 错误，我们需要选择高精度，而如果我们的目标是最小化类型 2 错误，那么我们应该选择一个阈值，使得召回率很高。

精度分母是一个变量：即假阳性（归类为阳性的负样本）每次都会变化。

召回分母是一个常数：它代表真值的总数，因此将始终保持不变。

这就是为什么下图 Precision 在结束时有一个波动，而召回始终保持平稳的原因。

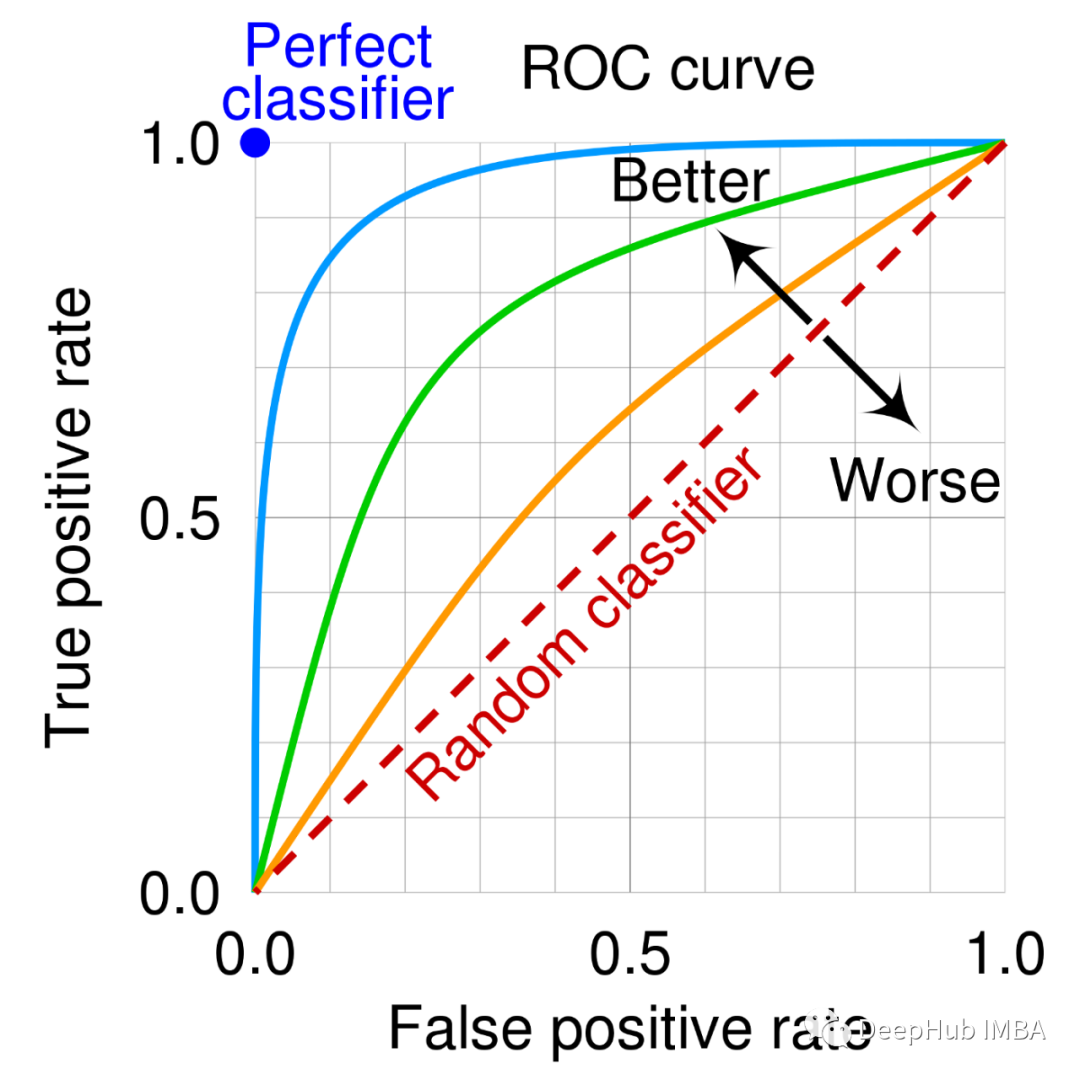
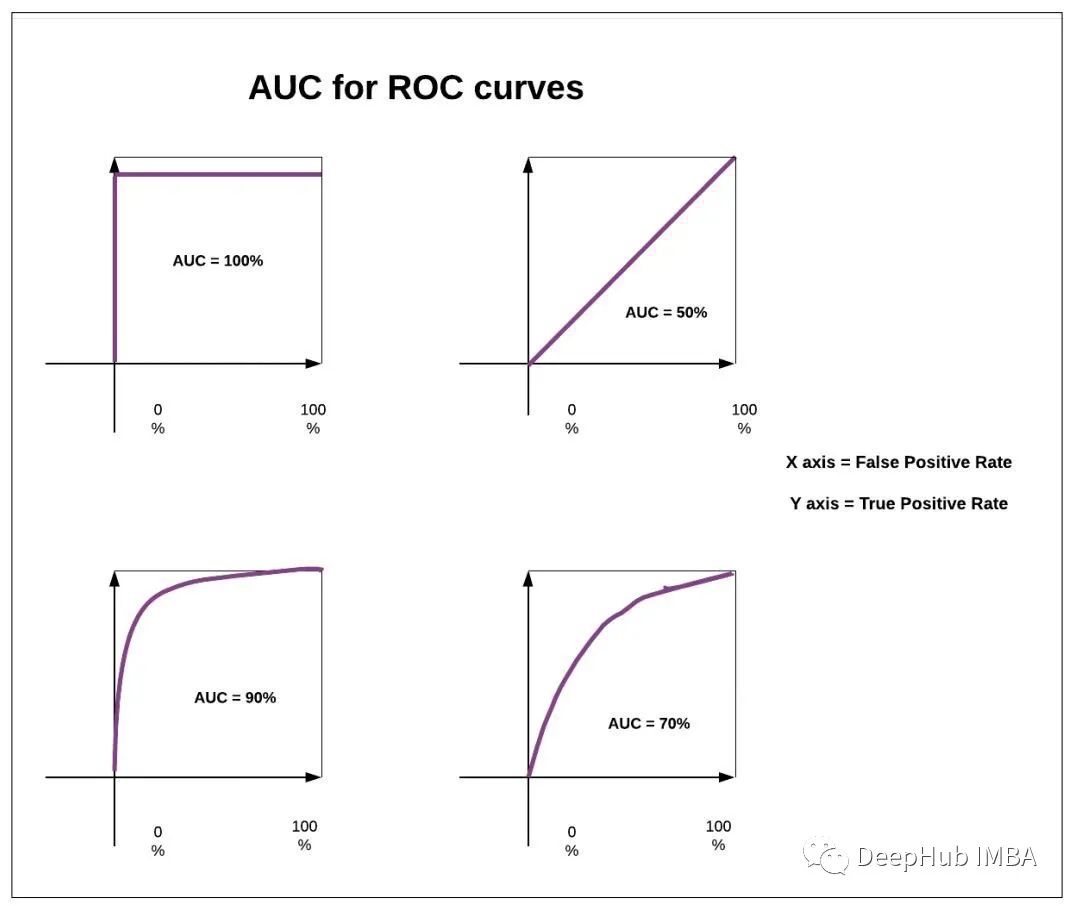
4、ROC曲线

ROC 曲线是显示分类模型在所有分类阈值下的性能的图表。

这条曲线绘制了两个参数：

真阳性率误报率

此曲线下的面积（称为 AUC），也可用作性能指标。AUC 越高，模型越好。

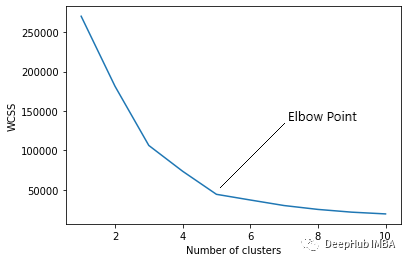
5、弯头曲线（K-Means）

用于K-means算法中最优簇数的选择。

WCSS（簇内平方和）是给定簇中每个点与质心之间的平方距离之和。当我们用 K（簇数）值绘制 WCSS 时，该图看起来像一个肘部（弯头）。

随着聚类数量的增加，WCSS 值将开始下降。K = 1时WCSS值最大

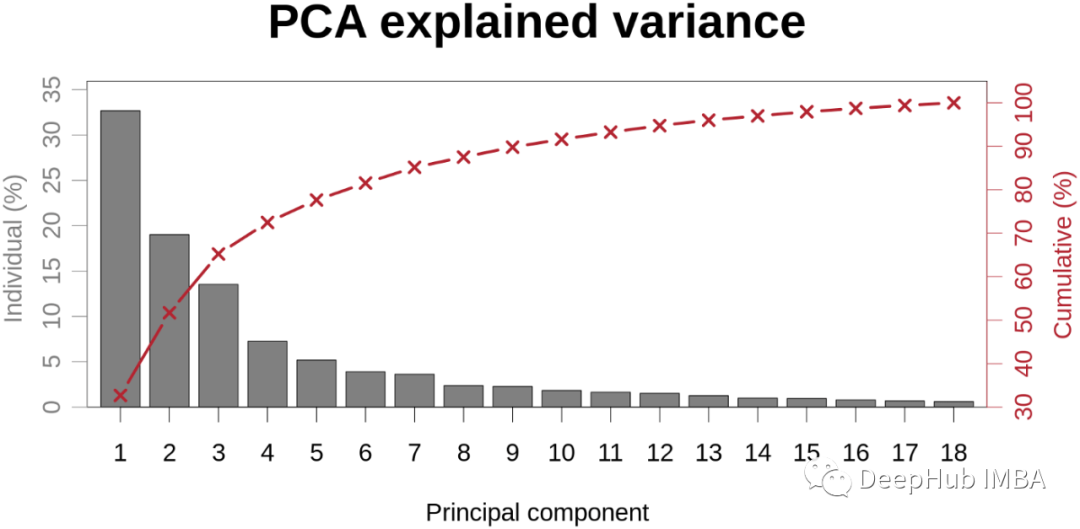
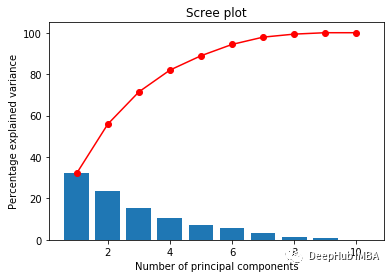
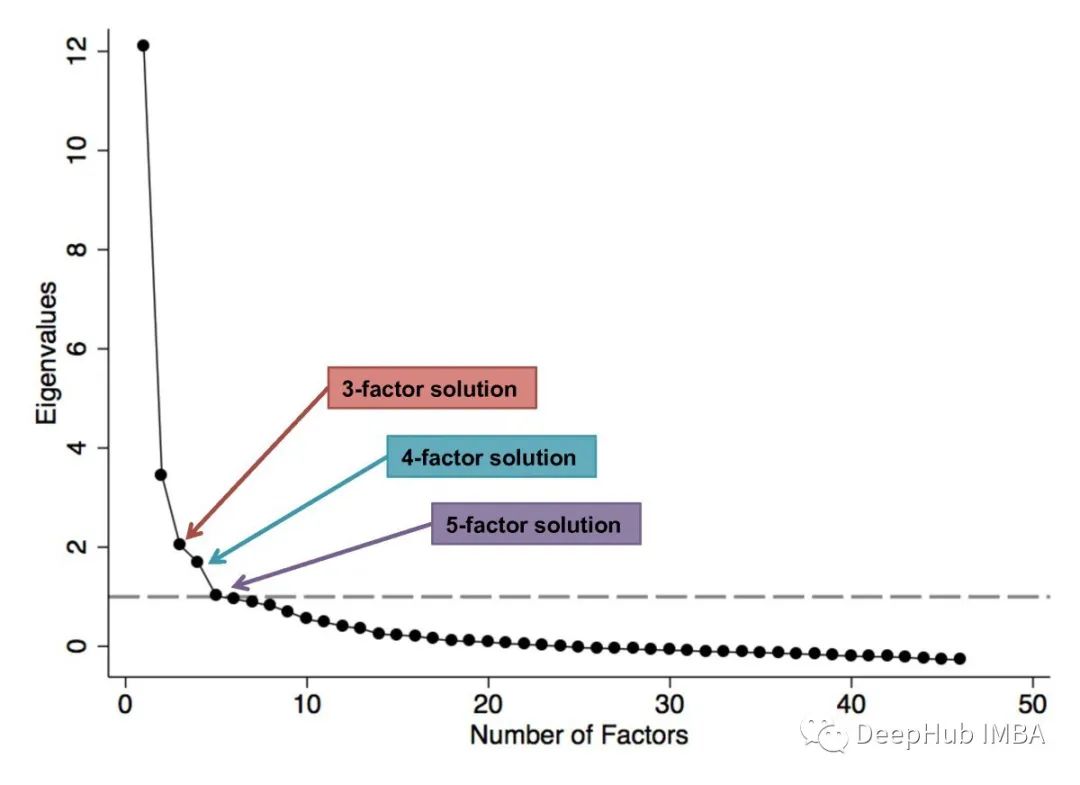
6、Scree Plot (PCA)

它帮助我们在对高维数据执行主成分分析后，可视化每个主成分解释的变异百分比。

为了选择正确数量的主成分来考虑我们的模型，我们通常会绘制此图并选择能够为我们提供足够好的总体方差百分比的值。

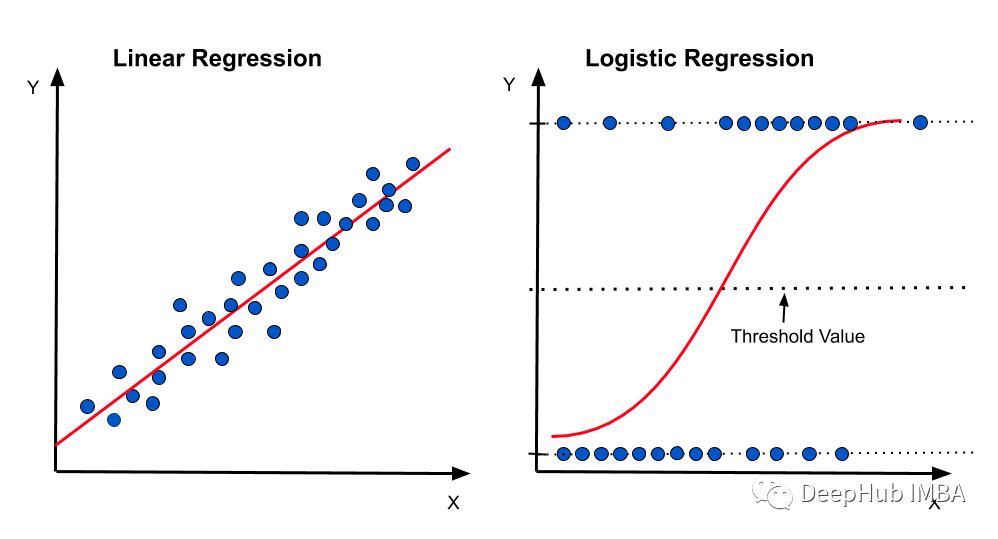
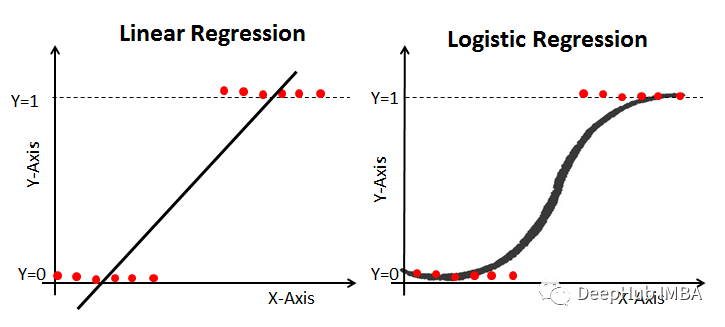
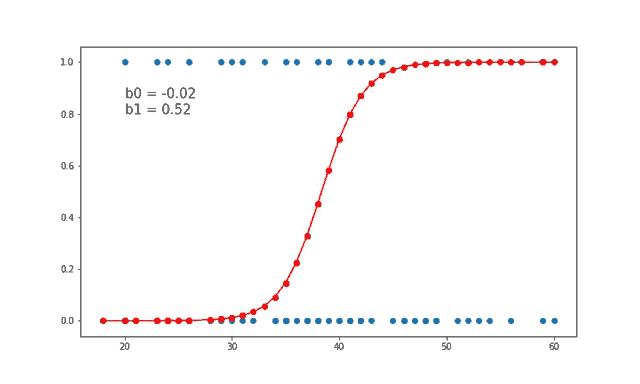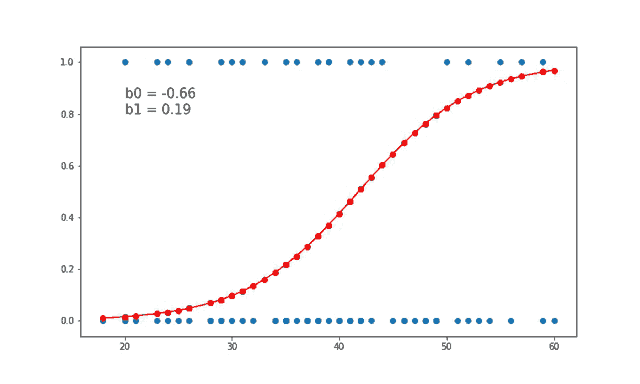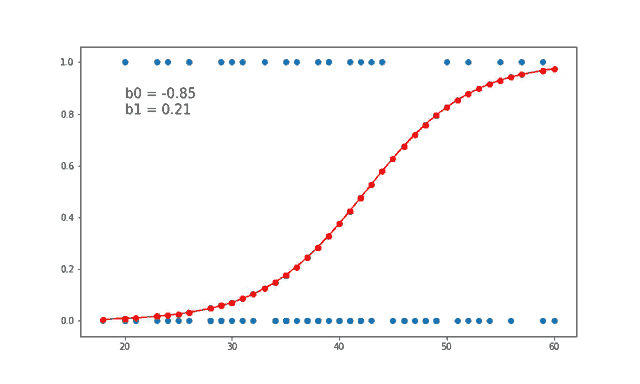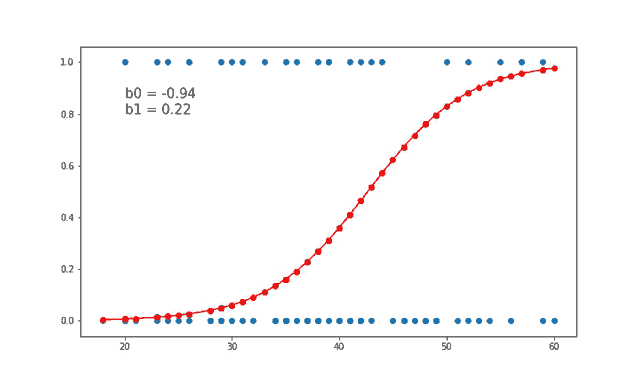
7、线性和逻辑回归曲线

对于线性可分数据，我们可以进行线性回归或逻辑回归，二者都可以作为决策边界曲线/线。

但是，在逻辑回归的情况下，由于通常只有 2 个类别，因此具有线性直线决策边界可能不起作用，在一条直线上值从低到高非常均匀地上升，因为它不够陡峭在值突然上升后会得到很多临界的高值或者低值，最终会错误分类。因此，“边界”区域，即概率从高到低转变的区域并不真正存在。所以一般情况下会应用 sigmoid 变换将其转换为 sigmoid 曲线，该曲线在极端情况下是平滑的，在中间几乎是线性的。

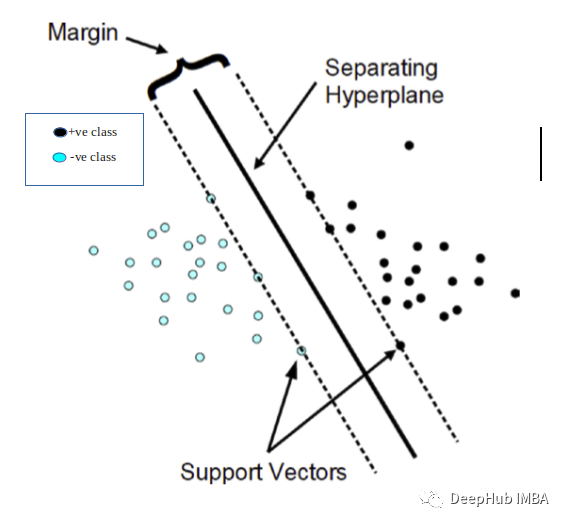
8、支持向量机(几何理解)

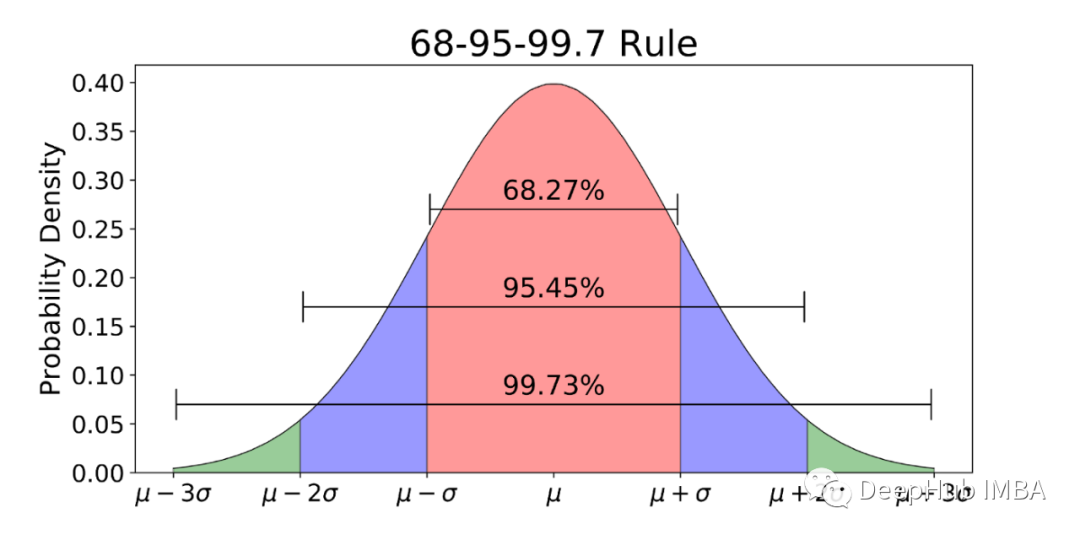
9、标准正态分布规则(z -分布)

均值为0，标准差为1的特殊正态分布。

经验法则指出，按照正态分布观察到的数据中有 99.7% 位于平均值的 3 个标准差以内。

根据该规则，68% 的数据在一个标准差内，95% 在两个标准差内，99.7% 在三个标准差内。

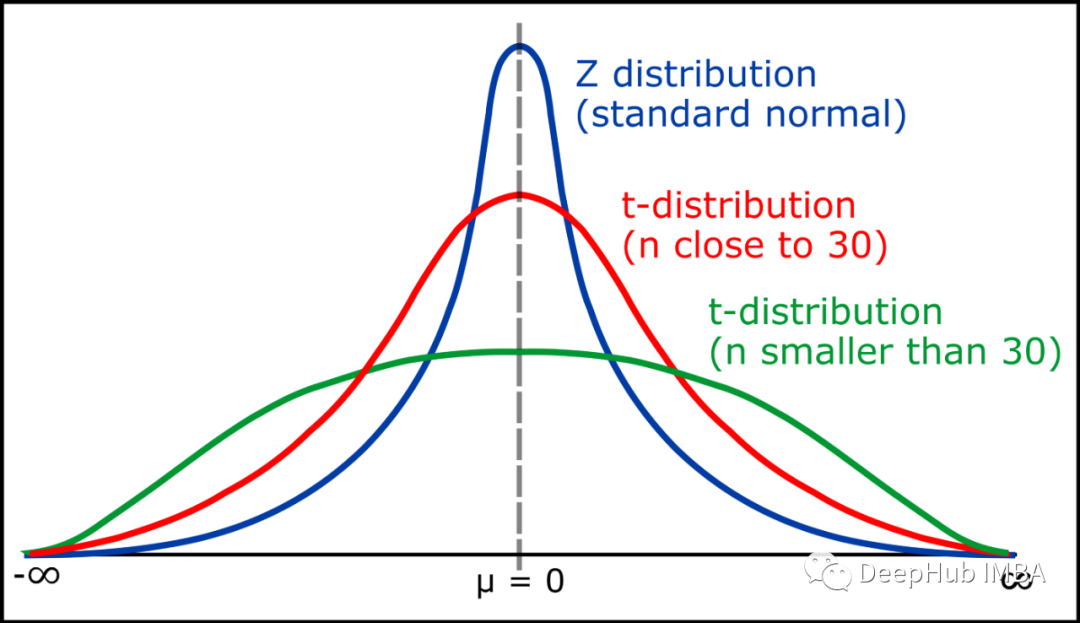
10、学生 T 分布

T 分布（也称为学生 T 分布）是一系列分布，看起来几乎与正态分布曲线相同，只是更短和更宽/更胖。

当我们有较小的样本时，我们使用 t 分布而不是正态分布。

样本量越大，t 分布越像正态分布。事实上，在 30 个样本之后，T 分布几乎与正态分布完全一样。

最后总结

我们可能会遇到许多小而关键的概念，这些概念构成了我们做出决定或选择正确模型的基础。本文中提到的重要概念都可以通过相关的图表进行表示，这些概念是非常重要的，需要我们在看到其第一眼时就知道他的含义，如果你已经对上面的概念都掌握了，那么可以试试说明下图代表了什么：

点「在看」的人都变好看了哦！