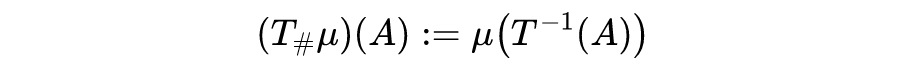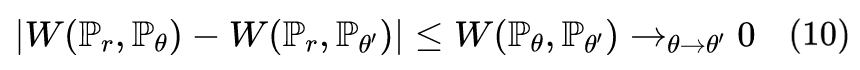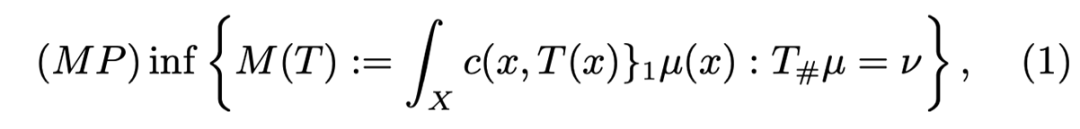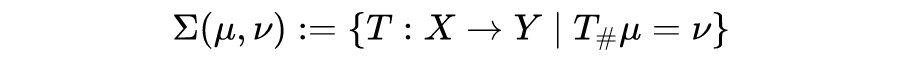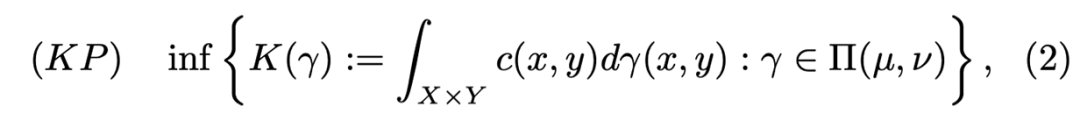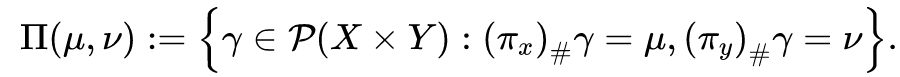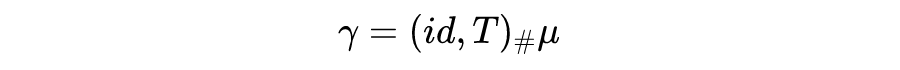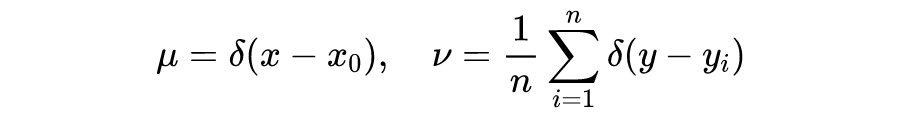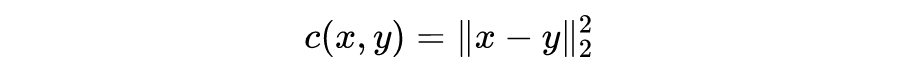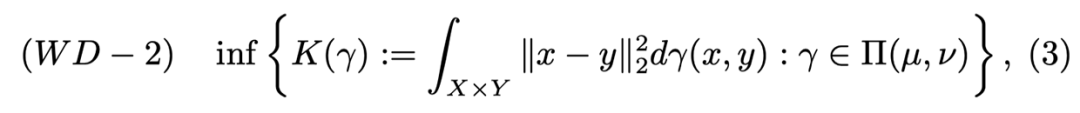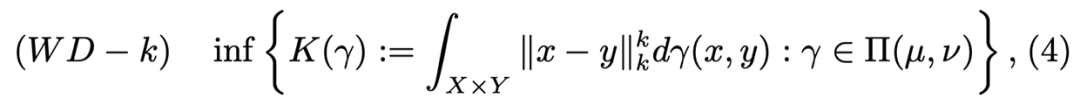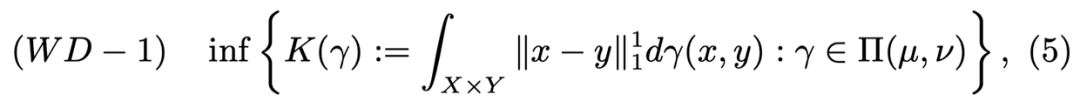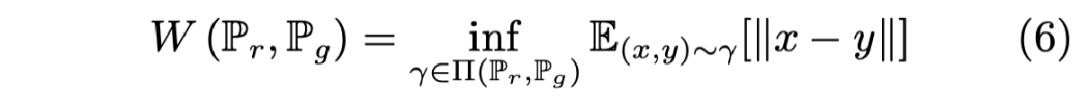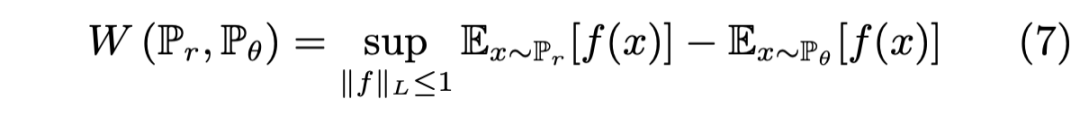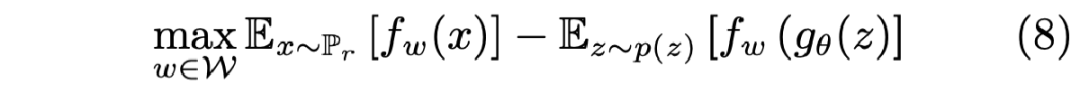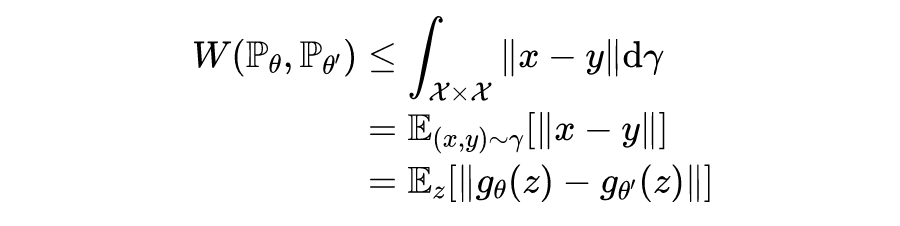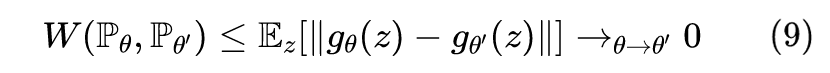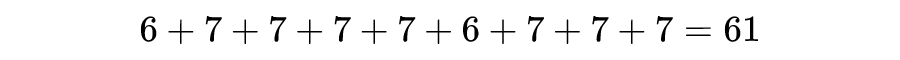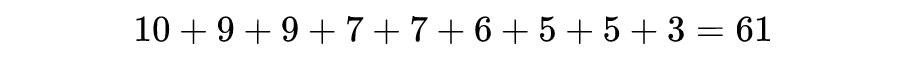一文详解Wassertein距离

©PaperWeekly 原创 · 作者｜孙裕道

学校｜北京邮电大学博士生

研究方向｜GAN图像生成、情绪对抗样本生成

引言

WGAN 的横空出世引出了一个更好度量两个概率分布差异的指标即 Wassertein 距离（或叫做推土机距离），它主要优势就在于该距离具有连续性的特质。TV 散度和 JS 散度的缺点在于这两个距离不具有连续性，这会导致在神经网络参数优化的过程中梯度会消失，KL 散度则是因为该距离不具有对称性即 。

本文会从 Monge 问题开始详细介绍关于 Wassertein 距离的一些相关背景和证明，最后给出了一个实例有助于理解 Wassertein 距离这个概念。

Monge问题（最优传输映射）

一般情况下，假定   和   是完备、可分的度量空间，例如欧式空间的子集  ，通常是紧集。  代表   上所有概率测度构成的空间。

问题1（Monge 问题或最优传输问题） 给定两个概率测度  ，  和一个代价函数  :  ，求：

其中由映射   诱导的推前测度   定义为：

这里   是任意可测集合，映射空间：

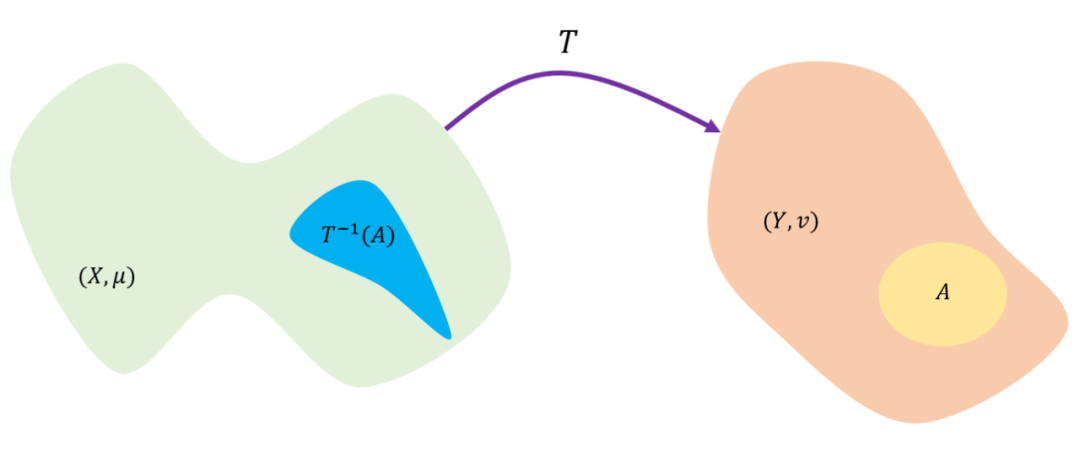
如下图示，Monge 问题其实是在找一个最优传输映射  ，映射   将空间   映射为空间  ，  是空间   中的区域，  是   在   中原像。需要满足的条件是对于   空间中区域   的测度要与   空间中区域   的测度要相等。根据下图通俗易懂的理解是面积   在   中的占比与面积   在   中的相等。

Kantorovich问题（最优传输方案）

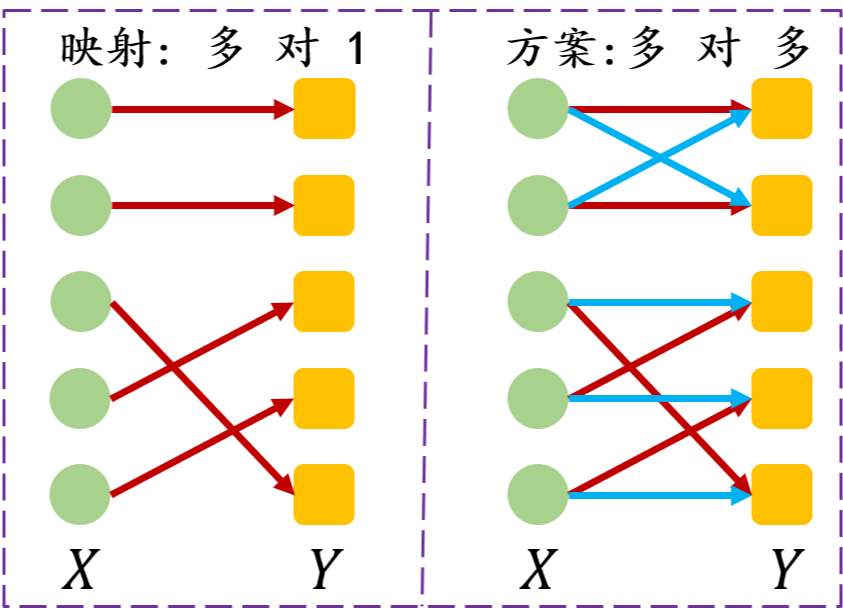
对于 Monge 问题，由于需要求解一个映射，实际上只能允许多对一或者一对一（映射的定义），Kantorovich将传输映射放松成传输方案，允许一对多，从而将原来问题进行简化。

假定有一个联合概率分布  ，其边际概率分布分别等于  和  ， ， ，这里   和   是投影映射： 。

问题2（Kantorovich 问题或最优传输方案问题）给定两个概率测度  ，  和一个代价函数  :  ，求解：

其中联合概率测度   属于传输方案空间：

如果一个最优传输映射为  ，则最优传输方案   有如下形式：

给定离散的   和  ，可能不存在任何传输映射：

但传输方案总是存在的，例如  。所以说 Kantorovich 问题是 Monge 问题的一个弱化和放松。如下图所示，图中左半部分是映射，映射的要求是   空间中的元素有且只有一个   空间中的元素与之对应。图中的有右半部分是方案，方案可以是多多的形式。

Wassertein距离

4.1 Wassertein距离定义

在深度学习中利用最优传输代价作为统计散度来反应两个概率密度之间的离散程度。主要用来表示两个概率分布的不相似程度，类似的统计散度有比较知名的 KL 散度，JS 散度，还有一种度量概率分布很好方式就是利用 Wassertein 距离。

如果将 Section 3 的 Kantorovich 问题的公式（2）里的代价函数   换成欧式距离：

就得到了 2-Wassertein 距离：

类似的，对于任意正整数  ，k-Wasserstein 距离可以定义为：

其中，  是   范数，即  ， 。

我们最熟知的推土机距离（Earth-Mover）为 1-Wassertein 距离：

将公式（5）写成期望的形式为：

其中   表示边缘分布   和   的所有联合分布   的集合。  可以理解为将分布   转换成分布   所消耗的成本的方案。

我们熟知的 WGAN 的对抗目标损失其实是公式（6）的对偶形式，具体公式如下所示：

其中上确界在所有 1-Lipschitz   的上面。如果将   替换为  ，则会有一个参数化的函数  ，进而可以求解问题：

其中，  为神经网络的参数。

4.2 Wassertein距离连续性

Wassertein 距离衡量分布的一个最大的好处就在于它距离度量的连续性。

证明：

假定   和   是   中的两个参数向量，其中联合的分布   的集合为  。

由公式 6 的 Wassertein 距离的定义可知：

如果   在   中是连续的，那么  ，则有  ，由于   是紧的，其中任意两个元素的距离必须由某个常数   一致有界，因此对于所有   和  ，  一致。根据有界收敛定理，则有：

最终则有：

连续性证明完毕。

4.3 Wassertein距离实例

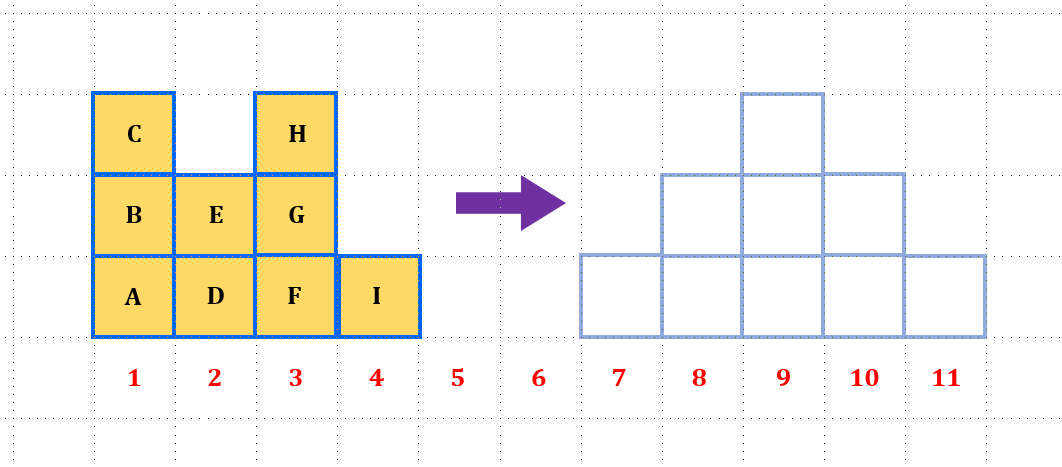
如下图所示考虑怎样将下面左图中的（实线）方块区域搬到右图中的（虚线）方块区域中，并且综合所移动距离最短。我们可以把这里的移动距离（或者传输距离）堪称是位置之间的距离差。比如左边的方块 I 在位置 4，如果搬到右边的位置 11，那么距离就是 7。

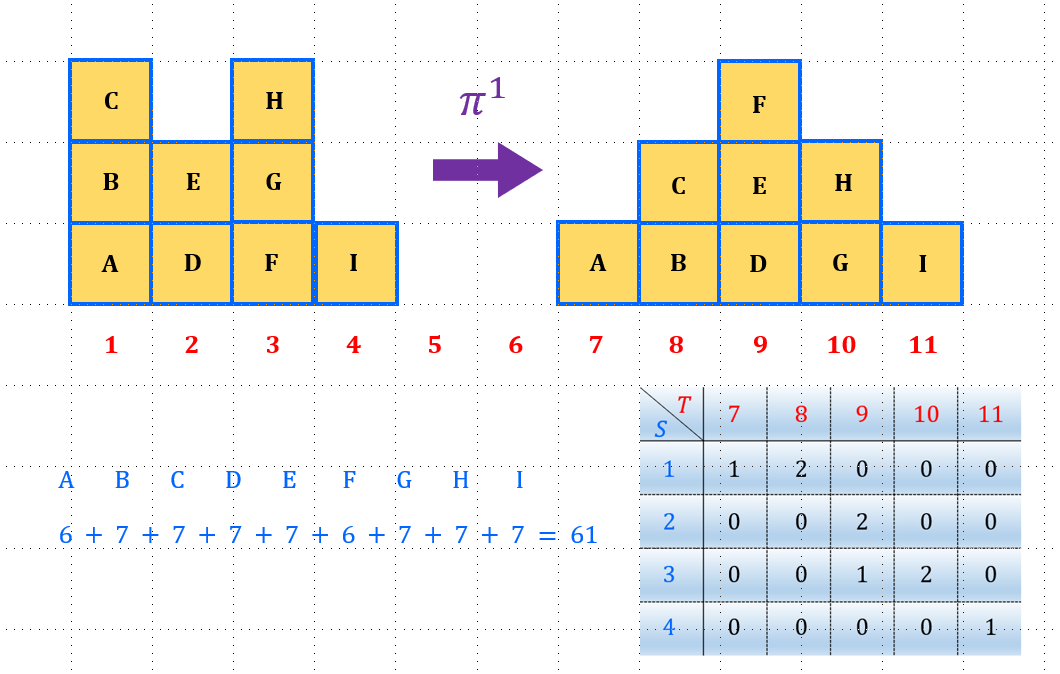
对于上图的问题，我们的一个直观的感受就是有很多种的搬运方块的方案。搬运方案一如下图所示，我们可以把位置 1 的方块 A，放到位置 7 处，剩下两个方块 B 和 C 放到位置 8 中；位置 2 处的方块 D 和 E 放到位置 9 处；位置 3 的方块 F 放到位置 9 处，剩下的两个方块 H 和 G 放到位置 10 处；位置 4 的方块放到位置 11 处。搬运方案一总体的运输距离为：

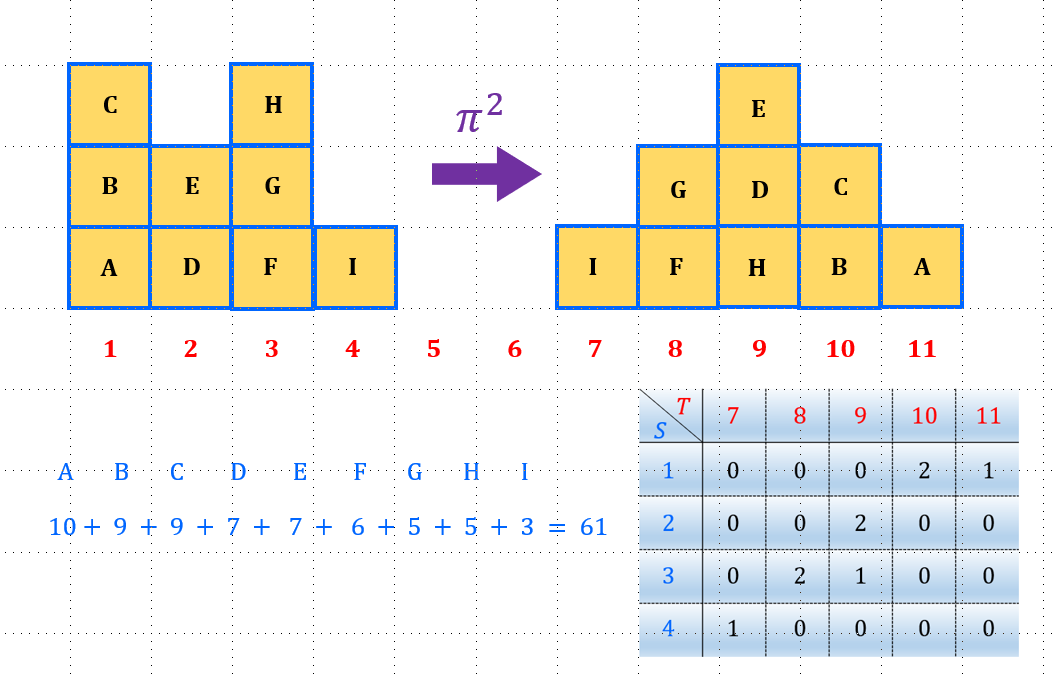
搬运方案二如下图所示，我们可以把位置 1 的方块 A，放到位置 11 处，剩下两个方块 B 和 C 放到位置 10 中；位置 2 处的方块 D 和 E 放到位置 9 处；位置 3 的方块 H 放到位置 9 处，剩下的两个方块 F 和 G 放到位置 8 处；位置 4 的方块放到位置 7 处。搬运方案二总体的运输距离为：

上面两种运输方案的运输距离是一样的。最优传输方案就是遍历所有的传输方案找出传输代价最小的传输方案。

更多阅读

#投 稿 通 道#

 让你的论文被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。

📝 来稿标准：

• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向） 

• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接 

• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志

📬 投稿邮箱：

• 投稿邮箱：hr@paperweekly.site 

• 所有文章配图，请单独在附件中发送 

• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。