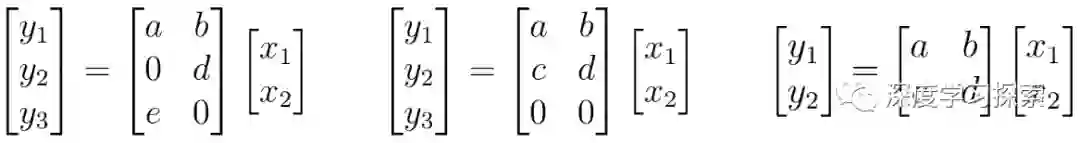MorphNet：走向更快，更小的神经网络

2019 年 8 月 13 日 深度学习探索

深度神经网络（DNN）已经证明在解决实际相关的难题（如图像分类，文本识别和语音转录）方面具有显着的效果。然而，为给定问题设计合适的DNN架构仍然是一项具有挑战性的任务。考虑到可能的架构的大搜索空间，从头开始为您的特定应用设计网络在计算资源和时间方面可能非常昂贵。神经架构搜索和AdaNet等方法使用机器学习来搜索设计空间，以便找到改进的架构。另一种方法是针对类似问题采用现有架构，并在一次性中针对手头的任务对其进行优化。

在这里，我们描述MorphNet，一种用于神经网络模型细化的复杂技术，采用后一种方法。最初在我们的论文“MorphNet：深度网络的快速和简单的资源约束结构学习”中提出，MorphNet将现有的神经网络作为输入，并生成一个更小，更快，并为新的定制的更好的性能的新神经网络问题。我们已将该技术应用于Google规模的问题，以设计更小，更准确的生产服务网络，现在我们向社区开放了MorphNet的TensorFlow实施，以便您可以使用它来使您的模型更多高效。

如何运作

MorphNet通过缩小和扩展阶段的循环来优化神经网络。在缩小阶段，MorphNet识别低效神经元并通过应用稀疏正则化器从网络中修剪它们，使得网络的总损失函数包括每个神经元的成本。然而，MorphNet不是对每个神经元应用统一的成本，而是计算相对于目标资源的神经元成本。随着训练的进行，优化器在计算梯度时会意识到资源成本，从而了解哪些神经元具有资源效率，哪些神经元可以被移除。

作为示例，考虑MorphNet如何计算神经网络的计算成本（例如，FLOP）。为简单起见，让我们考虑一个表示为矩阵乘法的神经网络层。在这种情况下，该层具有2个输入（xn），6个权重（a，b，...，f）和3个输出（yn;神经元）。使用乘以行和列的标准教科书方法，您可以确定评估此图层需要6次乘法。

MorphNet将此计算为输入计数和输出计数的乘积。请注意，尽管左侧的示例显示了权重稀疏度，其中两个权重为0，但我们仍需要执行所有乘法来评估此图层。但是，中间的例子显示了结构化的稀疏性，其中神经元yn的行中的所有权重都是0. MorphNet识别出该层的新输出计数为2，并且该层的乘法数从6减少到4。这个想法，MorphNet可以确定网络中每个神经元的增量成本，以产生一个更有效的模型（右），其中神经元y3已被删除。

在扩展阶段，我们使用宽度乘数来均匀地扩展所有图层大小。例如，如果我们扩展50％，那么以100个神经元开始并缩减为10的低效层将仅扩展回15，而仅缩小到80个神经元的重要层可能扩展到120并且具有更多资源。上班。净效应是将计算资源从网络中效率较低的部分重新分配到可能更有用的网络部分。

在萎缩阶段之后，人们可以停止MorphNet，以简单地削减网络以满足更严格的资源预算。这导致在目标成本方面更有效的网络，但有时可能导致准确性降低。或者，用户也可以完成扩展阶段，这将与原始目标资源成本相匹配，但具有更高的准确性。我们稍后将介绍这个完整实现的示例。

为何选择MorphNet？

MorphNet提供四个关键价值意见：
有针对性的正规化：
MorphNet对正规化采取的方法比其他稀疏正则化指标更有意义。
特别是，用于诱导更好的稀疏化的MorphNet方法旨在减少特定资源（例如每推理的FLOP或模型大小）。
这使得能够更好地控制由MorphNet引起的网络结构，这可以根据应用领域和相关约束而显着不同。
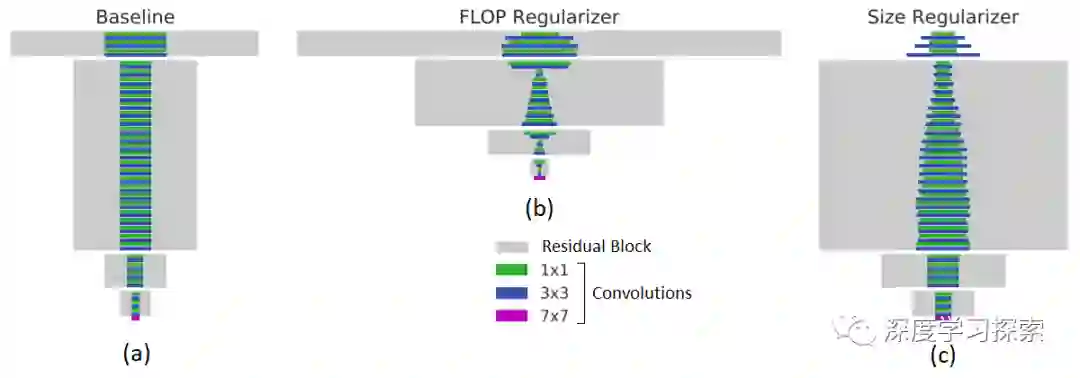
例如，下图的左侧面板显示了一个基线网络，其中包含在JFT上训练的常用ResNet-101架构。
MorphNet在针对FLOP（中心，减少40％FLOP）或模型大小（右侧，权重减少43％）时生成的结构有很大不同。
当优化计算成本时，网络较低层中的较高分辨率神经元往往比较高层中的较低分辨率神经元被修剪。
当针对较小的模型尺寸时，修剪权衡则相反。

MorphNet的目标正规化。矩形宽度与图层中的通道数成比例。底部的紫色条是输入图层。左：用作MorphNet输入的基线网络。中心：输出应用FLOP正则化器。右：输出应用大小正规化器。

MorphNet是少数几种可以针对特定参数进行优化的解决方案之一。这使它能够针对特定实现的目标参数。例如，通过合并特定于设备的计算时间和存储器时间，可以将延迟作为原始方式的一阶优化参数。

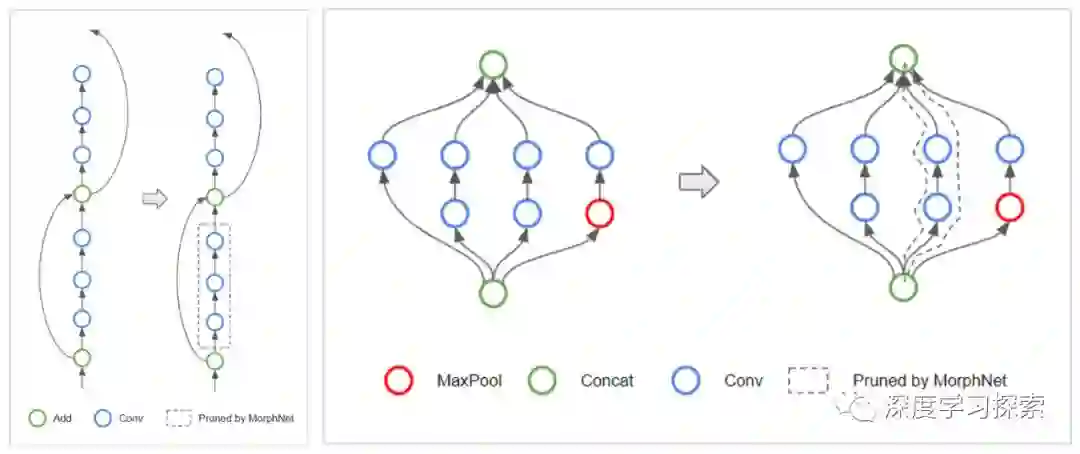
拓扑变形：当MorphNet了解每层神经元的数量时，该算法可能遇到一个特殊情况，即稀疏层中的所有神经元。当一个层有0个神经元时，这会通过从网络中剪切受影响的分支来有效地改变网络的拓扑。例如，在ResNet架构的情况下，MorphNet可能会保留跳过连接但删除残余块，如下所示（左）。对于Inception风格的体系结构，MorphNet可能会删除整个并行塔，如右图所示。

左：MorphNet可以删除ResNet风格网络中的残留连接。右：它还可以删除Inception风格网络中的并行塔。

可扩展性：MorphNet在单次培训中学习新结构，当您的培训预算有限时，这是一种很好的方法。MorphNet还可以直接应用于昂贵的网络和数据集。例如，在上面的比较中，MorphNet直接应用于ResNet-101，最初是在JFT上训练的，费用为100个GPU月。
可移植性：MorphNet生成的网络是“可移植的”，因为它们旨在从头开始重新训练，并且权重与架构学习过程无关。您不必担心复制检查点或遵循特殊培训配方。只需像往常一样训练您的新网络！

变形网络

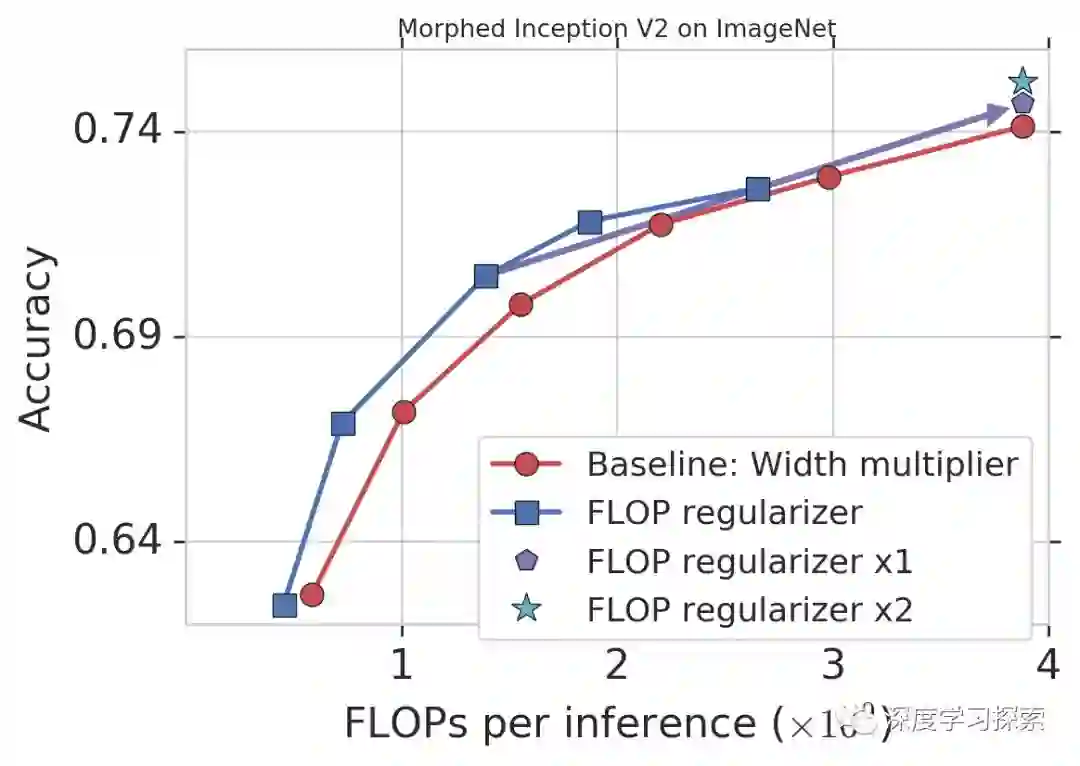
作为演示，我们通过定位FLOP将MorphNet应用于在ImageNet上训练的Inception V2（见下文）。基线方法是使用宽度乘数来通过统一缩小每个卷积的输出数量（红色）来折衷精度和FLOP。MorphNet方法直接针对FLOP，并在收缩模型时产生更好的权衡曲线（蓝色）。在这种情况下，FLOP成本降低了11％至15％，与基线相比具有相同的精度。