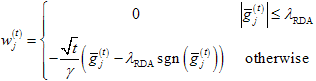带L1正则约束的优化

2018 年 2 月 20 日 KingsGarden Mr. King

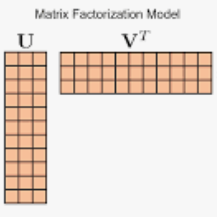
前言：断更了4个月，心里着实有点过意不去。趁着过年的这段空闲时间，把之前挖的坑给埋上。先简要回忆下上回内容里所说的。在上一回的内容中提到了稀疏编码的几个主要作用：1）数据压缩；2）分类；3）提高检索效率。介绍了两种可以获得稀疏编码的方法：矢量量化（Vector Quantization）和非负矩阵分解（Non-negativeMatrix Factorization）。其中矢量量化的核心思想是通过获得数据的编码簿（codebook），进而获得样本点所对应的分类信息。这里的稀疏编码对应的就是分类信息。非负矩阵分解的核心思想是获得表示样本点的一组基，通过非负约束，这组基向量具有稀疏以及对局部特征的良好性质，部分解决了表示学习的结果通常不具有可解释性的问题。而今天我们将主要介绍获得稀疏变量的一种主要方法—L1正则优化。

1 什么是L1正则约束

L1正则约束是直接产生稀疏编码的一种方法，对于需要进行稀疏约束的变量w，在L1正则中将变量w的所有项取其绝对值相加，并希望这个相加值在优化过程中最小。为此，通过L1正则约束后的变量w中会大量出现值为0的项，从而达到变量w稀疏的情况。加入L1正则约束后的优化目标为：

（1）

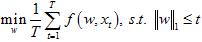
或者

（2）

其中T表示观测样本数量，t表示某一观测样本的序号，函数f为输入为x_t，参数为w的目标函数，‖.‖₁表示L1正则约束。一般称第一个优化目标（公式1）为有限制条件的形式化，第二个目标（公式2）为无限制条件的形式化。L1正则约束的表述虽然简单，但对上述的两个目标函数的直接优化都是非凸优化，不易通过直接对梯度进行优化的方式获得结果。关于加入L1正则项后的优化方法有很多讨论，这里我主要介绍两种比较易于实现的方法，以供大家选择。

2 方法一：TG（Truncated Gradient）

TG由Langford于2009发表在JMLR上，这一优化非常简单明了，其核心思想为：在优化过程中L1正则项作为限制条件，将满足某一设定阈值的变量w直接截断为0，从而达到稀疏的目的。虽然这种比较“暴力”的截断可以达到稀疏的目的，但对变量进行截断之后可能会使得优化无法收敛，而TG的目标正是尝试解决这一问题。直接看TG的优化过程。

算法1：TG

输入：阈值θ≥0，序列g_t≥0，学习率η∈(0, 1)，截断轮K，观测样本O

初始化：w_j←0 (j=1, ... , d)

for t=1, 2, …

（截断）如果t mod K等于0

for 变量w_j (j=1, ... , d)

如果w_j>0并且w_j≤θ，则w_j←max{w_j−ηg_t, 0}

如果w_j<0并且w_j≥-θ，则w_j←min{w_j+ηg_t, 0}

end for

更新梯度：w←w+η▽f(w, x)

end for

输出：w

根据TG的优化过程，我挑选TG算法中比较重要的几个执行点进行解释：

1）不需要在每一迭代轮t中对参数w进行截断，如果截断过于频繁，则对目标函数的优化将无法收敛。而如果截断的频次过少，则达不到设置L1正则项的目的。在实际的实现过程中，令参数K表示每K轮进行一次截断，通过调整K的大小来确定截断频次。一般在实际应用中，K的取值以10为单位尝试选择，比如K=10,20,30,…；

2）选择截断函数为如下的分段函数形式：

这种形式的分段函数保证了截断过程不会过于激进，而是相对缓慢进行截断操作。下图的右侧展示的是TG中所用的截断函数的效果示意。而左侧则是直接截断的效果示意。

可以观测到这两种截断函数的明显不同；

3）序列g_t的设置。在TG算法中，我们会将截断函数中的参数g_t（α=g_t）随着迭代轮次的不同而变化。一般可以将序列g_t设置为g_t =ηKg，其中g为常数，且ηK远小于θ。为了简化TG的调参过程，在原文中，作者提出可以令g_t=θ；

4） θ的设置。在原文中，为了简化TG的调参过程，作者提出了两种设置方法：1）令θ= g；2）令θ=∞。

总的来说，TG算法的实现相对简单，很容易应用随机梯度下降法进行优化。但TG算法并不严格保证算法的收敛，不容易在变量w设置为较稀疏情况下实现快速收敛。为此，我将介绍第二种优化方法。

3 方法二：RDA（Regularized Dual Averaging）方法

由于直接优化引入L1正则项的目标函数较为困难，为此Xiao于2009年在NIPS上提出L1-RDA算法，其核心思想为：通过Bregman距离（Bregman Divergence）构造对公式2的对偶形式，通过对对偶形式的优化求解结果（具体的对偶求解过程略）。RDA算法可以描述为：

算法2：L1-RDA算法

输入：正则项系数λ≥0，稀疏增强参数ρ≥0，参数γ>0，观测样本O

初始化：w_j←0 (j=1, ... , d)

for t=1, 2, …

计算梯度：g_t=▽f(w^(t-¹⁾,x)

ḡ⁽^t)=(t-1)/t×ḡ⁽^t^-1) + 1/t×g^(t)

λ_RDA=λ+γρ/sqrt(t)

更新梯度：

end for

输出：w

在算法2中，sgn表示符号函数，当输入为正时，输出为1；输入为负时，输出为-1；输入为0时，输出为0。

L1-RDA算法的参数设置说明如下：

1）参数γ。这个参数主要控制算法的学习速率，该参数越小则学习率越大，收敛越快。同时也会使得所学的变量w的稀疏程度越大。一般地，这个参数可以为1000为单位进行调整；

2）参数ρ。这个参数主要配合参数γ控制阈值λ_RDA在迭代过程中初始值的大小。一般地，这个参数设置的量级为10^-3，也就是说，γρ一般为取值为[1,100]的数值；

3）参数λ。这个参数主要控制变量w的稀疏程度。一般地，这个参数的选择可以以数量级为单位进行变化，例如λ=0.001,0.01,0.1,1,10,…。

L1-RDA算法有良好的收敛性保证，同时也是适用于在线学习的算法，因此L1-RDA算法是一种普遍较为认可的带L1正则约束的目标函数的优化方法。

总结

以上两种方法都比较方便实现，也可以适用于同时需要优化L1和L2正则约束的场景。相较而言，TG算法的实现更为简单，较适用于对场景问题的探索。而L1-RDA算法则较为适合对带L1约束问题的高效优化。大家可按适用的场景选择。

参考文献：

Langfordet.al. Sparse Online Learning via Truncated Gradient. JMLR 2009.
Xiaoet.al. Dual Averaging Methods for Regularized Stochastic Learning and Online Optimization. JMLR 2010.

登录查看更多