告别曲线拟合：因果推断和do-Calculus简介

2018 年 5 月 26 日 论智

来源： Ferenc Huszár

编译：Bot

编者按：最近，贝叶斯网络之父、图灵奖获得者Judea Pearl出了一本新书《The Book of Why》，他在书中指出因果关系将如何给科学发展带来革命性的变化，并给人工智能带来彻底改变。2011年，Pearl凭借人工智能概率方法和因果推理算法收获图灵奖，但他之后似乎就和大部队脱离了，在研究道路上越跑越“偏”。在去年的NIPS大会上，Pearl做了演讲，直斥现有的机器学习基于盲目（model-blind）的统计学模型，只是又慢又呆的曲线拟合练习。面对行业的盲目之风，他自嘲道：我是AI社区的“叛徒”。

本文作者为twitter旗下Magic Pony团队的机器学习工程师。

记得上回Judea Pearl上头条的时候，还是NIPS 2017期间，媒体断章取义地拍下了他对着“空无一人的房间”演讲的一幕。虽然这幅“悲凉”的场景博得了几乎所有人的同情，大家纷纷在社交媒体上转发、反思，但事实上没人真正关心他在台上说了什么。

同样是去年会议期间，Ali Rahimi和Yann Lecun关于“AI是不是炼金术”的论战被各大媒体争相报道，但Pearl的因果推断却鲜有人提及。当看到老人“颓然”坐在椅子上的一幕时，比起好奇他的研究内容，多数人恐怕已经在八卦大师境遇的路上一去不返。

好在这一次，Pearl终于靠着“叛徒”这一恶名把人们的目光聚焦到了他的心血上。

因果推断（causal inference）是什么

首先，因果推断区分了人们可能想要估计的两种条件分布。简单来说，就是在机器学习中，我们通常只会估计一种分布，但在某些情况下，我们可能也需要估计第二种。

什么是第一种、第二种分布？

为了说清楚这个概念，假设我们从p(x,y,z,…)的联合分布中采样了一些独立同分布数据，现在我们手里有大量数据，有最好的工具（如深度学习），它们可以被用来充分估计这些采样数据的联合分布，或者指数分布、条件分布、边缘分布等其他统计学意义上的分布。

换句话说，我们假设p是已知的，易于推断的，而我们的目的是观察给定一个x后，变量y会发生什么变化。这就引申出两种表述：

观察p(y|x)：如果观察变量X取值于x，Y的相应分布是什么？这是我们常在监督学习中遇到问题，它是一个条件分布，可以从p(x,y,z,…)中计算出它的两个边缘概率：p(y|x) = p(x,y)/p(x)。相信所有人都不会对这个公式感到陌生，也都会计算。
介入p(y|do(x))：如果设X的值为x，那Y的相应分布是什么？这其实就是通过人为把X的值设为x来干预数据生成过程，但其余变量还是用原先的生成方式，以此观察Y的变化（请注意，数据生成过程与联合分布p(x,y,z,…)不同）。

p(y|x)和p(y|do(x))一样吗？

p(y|x)和p(y|do(x))不一样，它可以用几个简单的思想实验来验证。假设Y是咖啡机锅炉实际压力，大约在0到1.1巴（bar）之间，具体取决于它的工作时间；而X是内置气压计的读数。我们随机挑选一个时间点同时观察X和Y，在气压计准确的前提下，p(y|x)应该是以x为中心的单峰分布，伴随因测量噪声带来的偏差。

但p(y|do(x))实际上和x无关，它和锅炉压力的边缘分布p(y)相同。因为它是人为的把气压计的值定为某个值（如掰住指针不让它正确读数），不会对锅炉内压力Y造成任何影响。

总之，y和x是相关的，或者说在统计学上是相关的，如果有x，我们就能预测y；但y不受x影响，所以调整x的值不会影响y的分布。因此p(y|x)和p(y|do(x))很不一样，上面的例子只是冰山一角。当存在更多具有复杂相互作用的变量时，介入性观察条件与观察性条件之间的差异可能会更加细致和难以表征。

我们要哪一种分布？

具体问题具体分析，我们应该根据任务需要设法估计这两个分布中的一种。如果最终目标是判断或预测（即观察自然发生的x并推断y的可能值），那我们就该研究p(y|x)。这是我们已经在监督学习里做惯的事情，也是机器学习被Judea Pearl诟病为曲线拟合的一个原因。它在分类、图像分割、超分辨率、语音转录、机器翻译等领域均有出色表现。

如果我们的目标是根据估计的条件控制或选择x，那我们就该关注p(y|do(x))。比如设x为医院治疗方案，y是治疗结果，系统关注的不是随着治疗方案自然进行，治疗结果y的分布；而是通过不断控制x，来找出治疗方案对y会造成什么影响。类似的情况发生在系统识别、控制和在线推荐系统中。

p(y|do(x))究竟是什么？

p(y|do(x))实际上就是一个普通的条件分布，但它不是基于 p(x,z,y,…)的，而是p_do(X=x)(x,z,y,…)。这里的p_do(X=x)是我们如果实际进行干预的话会观察到的数据的联合分布。所以p(y|do(x))是从随机对照试验或A/B测试收集到的数据中学习的条件分布，其中x由实验者控制。

请注意，在很多时候，按上述所说的完全随机和完全手动控制是不可能实现的，它也是没有可操作性和不道德的。我们不能在人身上做A/B测试，让一半受试者吸食杂草末，另一半人吸大麻来了解毒品对健康的影响。

但即便不能从随机实验中直接估计p(y|do(x))，这个分布也是实际存在的。所以因果推断和do-calculus的主要观点是：

如果我不能在随机对照实验中直接测量p(y|do(x))，那我是否可以根据我在受控实验之外观察到的数据来估计它？

这些事情是如何相关的？

让我们从简单的p(y|x)开始说起：

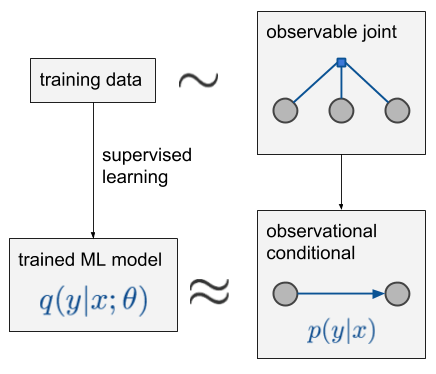
假设我们按x,z,y这个顺序观察数据，并从根据这3个变量观察到的数据分布中采样一部分独立同分布数据，把过程标记为蓝色因子图“observable joint”。如果你不知道什么是因子图，没关系，你只需知道图中的圆圈代表随机变量，小方块代表它连接的变量的联合分布。

我们要做的是根据x预测y，其中z是第三个变量，我们可以不管它（但一定要观察）。最后的observational conditional p(y|x)就是从这个分布中用简单条件计算出来的。对于左上那一大堆训练数据，我们可以建立一个模型q(y|x;θ)，用在深度网络中最小化交叉熵等方式计算一个近似值。

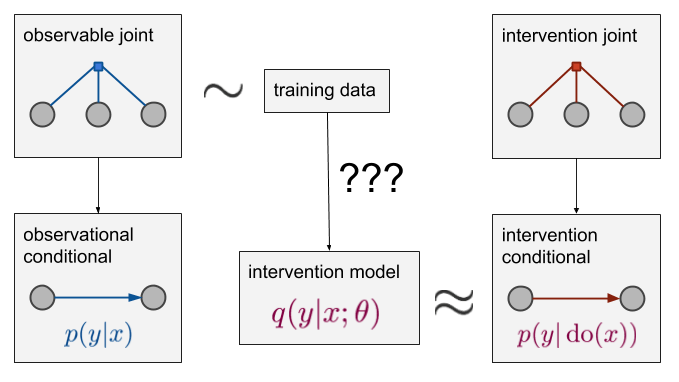
那么，如果要计算p(y|do(x))呢？

我们还是有蓝色的这些数据分布，数据也从这些分布中采样，但是这一次，我们要计算的目标成了右下角红色的p(y|do(x))，它只和红色的“observable joint”相关。这是一个和p有相同的域的联合分布，但它是一个不同的分布。如果我们能从红色数据分布中采样，这就又成了一个简单的监督学习问题。但这是不可能的，我们只有蓝色的。所以如果要计算p(y|do(x))，我们只能另寻它法。

因果模型

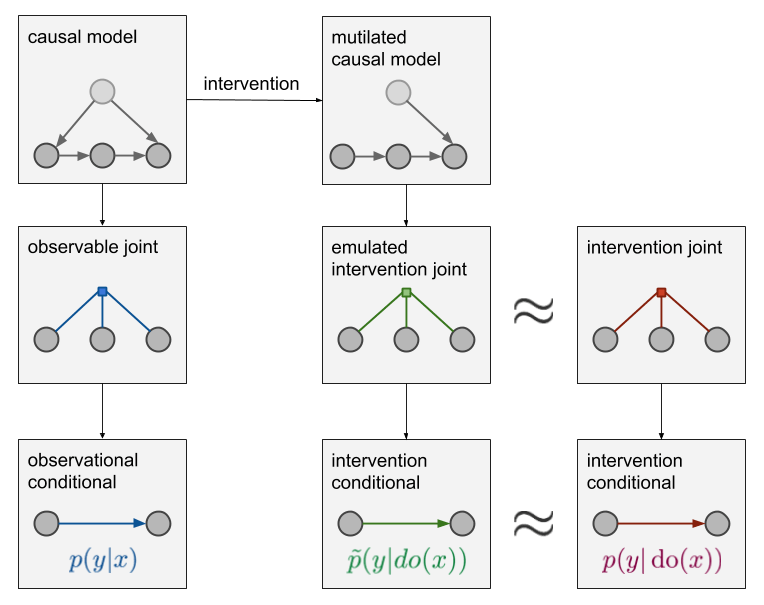
如果我们想要在蓝色和红色“observable joint”之间建立联系，那我们就必须对数据生成机制的因果结构进行额外的假设。我们要明确变量间的因果关系，这是预测分布变化的唯一方法。这种关于因果关系的信息并不仅仅存在于联合分布中，我们还得知道一些比这更有表现力的东西，如下图所示：

除了“observable joint”，现在我们多了一个全局因果模型（左上），它包含更多的细节：它不仅知道压力和气压计读数是相关的，还知道是气压上升导致读数上升，而不是读数上升导致气压上升。模型中的箭头对应于假设的因果方向，没有箭头表示变量之间没有直接的因果影响。从因果图到联合分布的映射是多对一的：几个因果图与相同的联合分布是一致的。因此，通过仅查看观察到的数据，我们不可能在不同的因果解释之间作出选择。

建立因果模型是一个建模的过程，我们必须先假设这个模型是怎么工作的，什么导致了什么。一旦画出因果关系图，我们就能通过破坏因果网络来模拟干预的效果：删除导致do操作的所有节点的所有边。上图中的绿色observational conditional表示被破坏后因果模型的联合分布，它的条件分布是p̃(y|do(x))，可以被用来估算p(y|do(x))的近似值。如果我们得到了定性的因果结构（即没有缺失节点并且箭头的方向都是正确的），那么这个近似就是精确的并且p̃(y|do(x))=p(y|do(x))。如果因果假设是错误的，那么近似值也是错误的。

重要的是，如果我们要得到这种绿色的分布，我们就必须将数据与其他假设相结合，或者说是使用先验。如果做的到，你可以这么做，但数据本身没有提供这类假设。

Do-calculus

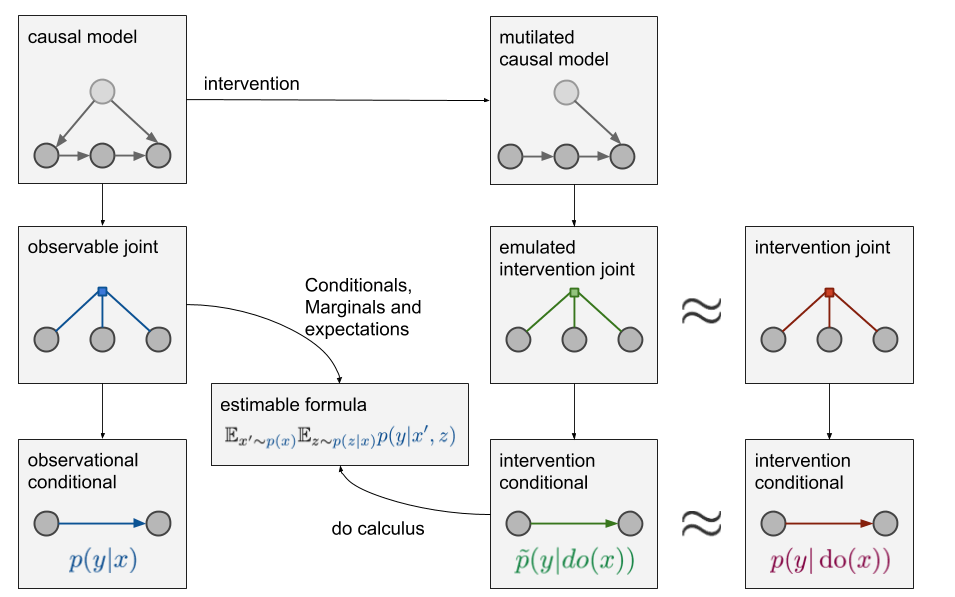
现在的问题是，当只有蓝色分布中的采样数据时，我们该怎么凭空造出绿色分布中的数据。相比之前，现在我们多了两个相关的因果模型，这时就要用到do-calculus。它允许我们慢慢探索绿色条件分布，直到我们可以根据蓝色分布下的各种边际分布、条件分布和期望来表示它。考虑到其中的细节太过复杂，这里我们只能说do-calculus确实有用、能用，具体内容请参考这篇论文：Introduction to Judea Pearl’s Do-Calculus。

理想情况下，最后我们能获得一个p̃(y|do(x))的等价公式，这个公式中不再有任何do操作符，所以我们只需观测数据就能估计它。如果这个估计是可实现的，我们就认为因果查询p̃(y|do(x))是可识别的；如果不能实现，那因果查询就是不可识别的，我们就无法得出红蓝数据的因果关系。

上图中这个新出现的"estimable formula"表示经过数次do-calculus推导后得出的p̃(y|do(x))的等价式。需要注意的一点是，如果我们观察了变量x,z,y，但只关心p(y|x)，那么那个无关紧要的z还是可以被用来执行因果推断的。如果我们没有观察z，那监督学习照样实现，但p(y|do(x))就成未解之谜了。

我们的因果模型是正确的吗？

我们根本无法根据观察到的数据完全验证因果关系图的有效性和完整性，但我们可以从局部验证它是否是正确的。如因果关系图中可能暗示了变量集之间某些条件的独立性或依赖关系，它们可以被实证测试：如果它们不在数据中，因果模型就是错的。

但底线是：一个完整的因果模型是一种先验知识的形式，我们可以用分析获得因果问题的答案，但前提是没有实际进行干预。单纯的数据推理无法给出有意义的结论。与贝叶斯分析中的先验分析不同，因果推理必须具备因果关系图。在大多数情况下，如果没有它，我们就只是在做随机对照试验。

总结

因果推断关注的是一些基础问题，它能帮我们回答“如果我们对x做了什么，那……”的问题，而这些问题通常需要对照实验和明确的干预措施来解决。但截至目前，我们还没有找到足够好的实验方法。

在某些情况下，我们不需要考虑因果推断，只要正常推理就可以了，像强化学习等一些系统可以利用控制变量明确回避回答因果问题。但对于其他那些重要的应用，因果推断是唯一一种能从根本上解决问题的方法。

所以这里我们再强调一点，无论你关注的是因果推断还是深度学习，因果模型和do-calculus给我们带来的启示是要真正理解一个问题，根据你在因果图中捕获的假设，从数据中确定需要估计的东西。你可以继续用深度学习、SGD等，但事实上我们都应该同时关注这两方面的进展，这也是Judea Pearl始终在呼吁的一件事。

如果你开始对因果推断感兴趣了，下面是一些必读文献：

Counterfactual Prediction with Deep Instrumental Variables Networks
Multiple Causal Inference with Latent Confounding
Causal Effect Inference with Deep Latent-Variable Models
The Blessings of Multiple Causes
Estimating individual treatment effect: generalization bounds and algorithms
Matching on Balanced Nonlinear Representations for Treatment Effects Estimation
Deep Counterfactual Networks with Propensity-Dropout
Learning Weighted Representations for Generalization Across Designs
Deep-Treat: Learning Optimal Personalized Treatments from Observational Data using Neural Networks
DeepMatch: Balancing Deep Covariate Representations for Causal Inference Using Adversarial Training
Causal Generative Neural Networks
Discovering Causal Signals in Images