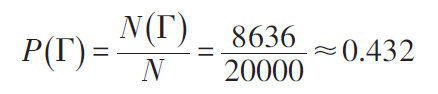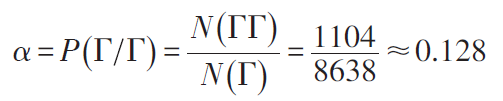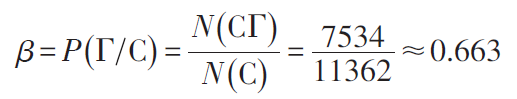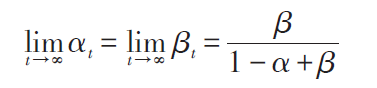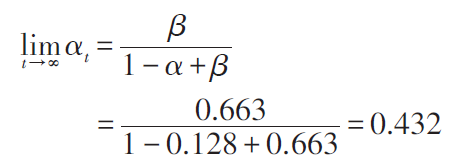【科技人文】马尔可夫的概率情怀

2018 年 5 月 21 日 科技导报

马尔可夫（1856—1922 年，图1）是俄罗斯数学家，圣彼得堡科学院院士，圣彼得堡数学学派的中坚。他深受圣彼得堡数学学派领袖切比雪夫（1821—1894 年）的学术影响，是切比雪夫概率思想的继承者和发展者。最初马尔可夫主要是沿着恩师开创的概率方向，致力于相互独立随机变量序列研究，改进和完善概率极限理论。后来其研究兴趣拓展到相依随机变量序列，创立和发展了著名的马尔可夫链理论，为随机过程发展奠定了基础。

图1 马尔可夫

爱吾师，但更爱真理

1874年，马尔可夫以优异成绩考入了神往已久的圣彼得堡大学数学系，开始自由“漫步”在绚丽多姿的数学王国。他很快就表现出独特的数学天赋，并被吸收到老师组织的讨论班参加学习。1878年，马尔可夫以优异成绩毕业并留校任教，其毕业论文荣获当年系里的金质奖。如鱼得水的马尔可夫一发不可收拾，越来越喜爱数学科学问题，一直攻读到博士研究生，分别于1880年、1884年获得硕士学位和博士学位。

1887 年，切比雪夫在论文“论概率论的两个极限定理”中，率先给出了中心极限定理及其证明。在概率论倍受西方科学界排挤的年代里，切比雪夫的研究工作让不少人幡然醒悟，但因其处理方法尚不够完善，故所得结果较为粗糙。由于切比雪夫在当时俄罗斯甚至国际上具有很高的学术声望，在较长一段时间内，无人质疑切比雪夫的相关论述。第1位指明了切比雪夫的定理叙述不严密且证明也不严格的是马尔可夫。

马尔可夫是切比雪夫的追随者和捍卫者。他秉承切比雪夫的学术研究传统方法，自1898年起就应用切比雪夫所采用的矩方法来研究概率极限理论，旨在应用传统数学方法，获得前辈和同时代数学家所取得的研究成果。这种追求平淡的理念需要娴熟的数学技巧需要付出艰辛的努力。

在反复推证定理过程中，马尔可夫很快就发现了切比雪夫的理论不严密之处。在给喀山大学教授瓦西里耶夫（1853—1929 年）的系列信函中，马尔可夫与之探讨了中心极限定理的相关理论。如在1898年10 月23 日的信中，马尔可夫明确指出切比雪夫的相关研究具有重要理论价值，但其不严密性却使论文价值有些失色。其中，他特别称切比雪夫所获结果为“正在证明的定理”，一方面表示对恩师的尊重和敬仰，另一方面则表明了其严谨的治学态度。可见，马尔可夫同亚里士多德（Aristotle，公元前384—公元前322）一样，表现出“吾爱吾师，但吾更爱真理”的大师风范。

此后，马尔可夫以“大数定理和最小二乘法”为题撰文，并发表于1898 年《喀山大学数理学报》。同年，在圣彼得堡科学院的院报上又撰文“论方程的根”，精确论述并证明了中心极限定理，其改进方法被称为“切比雪夫-马尔可夫矩方法”。

在概率论发展史上，马尔可夫应用矩方法第1次严格证明了中心极限定理，这充分表明了概率论同其他数学分支一样，拥有完美的逻辑基础和严密的数学论证。而当时，西方学界正极力把概率论排除在“科学殿堂”之外，正是圣彼得堡数学学派拯救了危难之中的概率论，使其恢复了数学科学地位。

同门竞技，共谱概率新篇章

在1900—1901年，马尔可夫的师弟李雅普诺夫（1857—1918 年）另辟新径，应用特征函数方法证明了中心极限定理，即“李雅普诺夫”定理。其证明方法不仅具有开创性，而且舍弃了随机变量序列所有阶矩皆存在的严格条件。当阶数趋于无穷时，这是矩方法难以企及的，故似乎利用矩方法理论难以达到特征函数法所得结论。

马尔可夫和李雅普诺夫都是切比雪夫的得意弟子，可谓之“左膀右臂”。他们曾并肩对抗数学家、神学家涅克拉索夫（1853—1924年）对圣彼得堡数学学派的学术攻击。马尔可夫很是佩服师弟的才华，师弟的成功使其再次直面中心极限定理，他试图仍然应用矩方法来获得李雅普诺夫的结论。这样马尔可夫不得不舍弃原定理基本条件，而寻觅新的研究途径。“千淘万漉虽辛苦，吹尽黄沙始到金。”马尔可夫经过多年的苦苦探索和艰苦努力最终获得了成功，最大限度地扩展了矩方法的应用范围，再次展现了传统数学方法的魅力，对此他感到很高兴，李雅普诺夫也给予了祝贺。

马尔可夫用矩方法来严格证明中心极限定理的系列研究主要体现在1908年发表的论文“切比雪夫不等式和基本定理”和“论李雅普诺夫院士所建立的概率极限定理”之中。前者讨论了若干定积分的连分数展开及其收敛性，论证了切比雪夫不等式；后者应用矩方法证明了李雅普诺夫定理，其中构建了一种新方法“截尾术”，即在适当领域截断随机变量使其有界，这样既不改变随机变量序列之和的极限分布，又能保证其任意阶矩存在，在结论部分，马尔可夫给出不适于所证定理的一个实例，但其适用于李雅普诺夫定理。这篇文章再次体现了马尔可夫的治学严谨性。

马尔可夫的“截尾术”不仅克服了李雅普诺夫“特征函数法”过分依赖随机变量独立性之弱点，开辟了通向非独立随机变量序列的研究道路，而且突破了特征函数仅适用于古典极限理论范畴的局限性，为强极限理论发展提供了有力概率手段。目前，“截尾术”与“对称化”以及“中心化”已成为现代概率极限理论的三大有力研究工具。

诗中觅芳，创立马尔可夫链

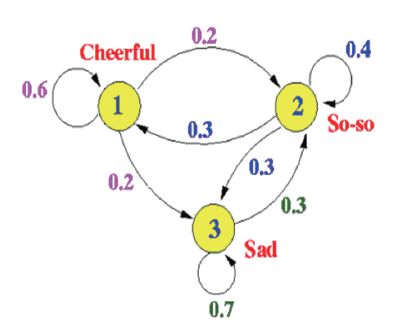
数学家的创新能力从何而来？为何其能发现新理论？为何能构建新学科来引导研究方向？根据中心极限定理可知，这是受诸多偶然和必然因素的影响，其中最重要的因素应当是厚积薄发的“灵光闪现”。多学科的相互融合能够开创新的研究领域，马尔可夫链（图2）就诞生于诗歌研究。

图2 马尔可夫链

1913年，马尔可夫应用概率思想分析了普希金（1799—1837 年）的长诗《叶甫盖尼·奥涅金》。诗人气势豪放，“其所以神化而超出于众表者，殆犹天马行空而步骤不凡”。马尔可夫把长诗看作是俄语字母的随机排列，并随机选取了其中连续排列的20000 个字母，用C代表辅音、Г代表元音（为了使问题简化起见，不妨把硬音、软音两个字母算作辅音），则诗人那火一般的诗篇犹如变成了一只池塘中的青蛙，从这片荷叶跳向那片荷叶，口中不时还叫上两声。马尔可夫分别统计了在C后面出现C和Г的频率以及在Г 后出现C 和Г 的频率。从中发现了元音字母和辅音字母的统计规律，据此估计出若干概率，如元音出现概率为

元音出现在元音后概率为

而元音出现在辅音后概率为

将所得结果与按照俄语拼音规则计算出的结果进行比较，证实了俄语中字母随机序列符合马尔可夫所建立的概率模型。如遍历性是马尔可夫链最简性质，即马尔可夫链的极限分布与初始状态无关。而在马尔可夫所统计的诗文情形中，则有

其中α_t，β_t是第t步的转移概率。将此公式应用于俄语中字母随机序列所形成的马尔可夫链，则有

此结果恰与诗文中元音出现的概率相等。

后来，马尔可夫还研究了俄罗斯19世纪现实主义作家阿克萨柯夫（1791—1859年）的《家庭纪事》，从中随机选取了100000个字母，其研究结果与此类似。因此，马尔可夫的论文“叶甫盖尼·奥涅金诗文的统计研究”，不仅应用语言学统计资料来阐明了马尔可夫链性质，更重要的是开创了数理统计语言学的研究先河。时至今日，文学著作的语言统计分析在国内外皆具卓有成效的研究成果。如《罗密欧和朱丽叶》的作者鉴定、《静静的顿河》作者是谁、《红楼梦》前80回和后40 回是否皆为曹雪芹所著等。更有甚者，应用统计学研究《毛泽东选集》也发现了不少规律。

刚正不阿，敢于挑战权威

除数学外，马尔可夫始终关心社会问题、热爱人文科学，总是做自己喜欢的事情，整个一生都是个反叛者。早在中学时期，他就经常读一些进步读物，为此与校方多次发生冲突。最严重的一次是在例行祈祷仪式上，马尔可夫不是把《圣经》捧在手中虔诚读诵，而是早早塞进了口袋盼着赶快离开。一直对马尔可夫有成见，并密切监视他的学监大声指责其破坏了宗教仪式的肃穆气氛，岂不知自己的咆哮声才是罪魁祸首。

马尔可夫的《概率演算》可谓是一部唯物主义者的战斗檄文。该宏著带有强烈论战性质，其主要对手竟是圣彼得堡数学学派元老布尼亚科夫斯基（1804—1889 年）和反动教会组织。虽在中学时代，马尔可夫就写信请教布尼亚科夫斯基，也是在其引导下报考了圣彼得堡大学数学系，然而在肯定布尼亚科夫斯基科学贡献的基础上，对于其宗教卫道士式言论，马尔可夫进行了毫不留情地批判，同时尖刻嘲讽地指出了其把概率论应用于供词、传说、候选人与意见间的各种选择及多数裁定司法判决等“伦理科学”实例。《概率演算》完全否定了上帝的存在，对于《圣经》也持怀疑态度，这在当时是“大逆不道”的著作。

1902年2月25日，圣彼得堡科学院文学部联席会议通过了一项决议，接纳被政府流放的高尔基（1868—1936 年）为名誉院士。然而，末代沙皇尼古拉二世却命令国民教育大臣，立即取消高尔基的院士资格。该科学院于3 月12 日不得不发布文告取消高尔基当选院士资格。科学院进步人士皆表示了强烈愤慨，马尔可夫也于4 月6日向院务委员会递交声明：“我认为科学院关于取消高尔基当选资格的文告是无效的和被强加的”，并论证了其依据所在。马尔可夫不仅强烈反对沙皇专制统治，并且觅到政治和数学的结合办法。

为转移国内日益高涨的革命情绪并准备帝国主义战争，沙皇政府于1913年以1613年罗曼诺夫当选沙皇为标志，庆祝罗曼诺夫王朝建立300周年。针对沙皇政府的浮华庆典，马尔可夫决定利用自己在科学界的威望，以1713年雅各布·伯努利《猜度术》出版为标志，发起了庆祝大数定理发现200周年的科学活动。

马尔可夫自己对大数定理理论很有研究。柯尔莫戈洛夫（1903—1987年）指出，马尔可夫大数定理的条件（1907 年提出）已很接近其于辛钦（1894—1959 年）在1929 年所得大数定理的必要条件。马尔可夫还把大数定理推广到相依随机变量序列，开创了相依随机变量的研究先河。

山水草木皆有韵，数学大美幻无穷。马尔可夫对数学充满了兴趣和感情，数学就是他生命中的主要组成部分，其以极为丰富的数学研究成果彰显着人类思维的魅力。值得一提的是，他把儿子也培养成了著名数学家。曾有人请教其数学的定义，他不假思索地答道：“所谓数学，就是高斯、切比雪夫、李雅普诺夫、斯捷克洛夫和我所从事的研究”。其中斯捷克洛夫是李雅普诺夫的得意门生，俄罗斯数学物理学派创始人。有趣的是，一般数学研究结果之冠名是由其他数学家认定，而马尔可夫则自己命名了“马尔可夫链”。这就是数学家的铮铮傲骨！

参考文献（略）