图池化经典之作: 18NIPS DiffPool

会员服务 ·

图池化经典之作: 18NIPS DiffPool

2020 年 2 月 11 日 图与推荐

作者: 张楚珩

单位: 清华大学交叉信息研究院

原文链接: https://zhuanlan.zhihu.com/p/106214278

DiffPool: Differentiable Pooling介绍了一种聚合图中的节点，从而学习到包含层级信息的图表示。

原文传送门

Ying, Zhitao, et al. "Hierarchical graph representation learning with differentiable pooling." Advances in neural information processing systems. 2018.

特色

在强化学习中，状态的表示学习是一个非常重要的问题，从专栏前面的一些文章里面我们了解到如果状态的表示具有一些好的性质的话，强化学习任务将会变得比较容易。在离散状态的情形下，我们常常能够使用图结构来表示状态之间的联系；在状态数目较多甚至无穷多（连续状态表示）的时候，应该如何学习到状态在图中的表示将会是一个比较有意思的问题。这里面涉及到很多问题，比如是学一个的 compact 表示还是学一个 abstraction，图里面每一个节点的定义究竟是什么，如何通过采样来学习到整个状态图的结构等。

其中，一个可能会面临的问题就是如何在图里面做节点的聚合；而这一篇文章就讲了一个可微分的节点聚合方案。

过程

1. 背景

图上的机器学习问题有这么几大类：node classification、link prediction、graph classification，分别对应对于图上节点和连边信息的提取，以及对于整个图全局信息的提取。图神经网络里面一类最重要的框架就是 neural message passing [1]，通过将图上的节点和邻近节点相互交互，从而实现对于图结构的信息抽取。如果我们是做 node classification 或者 link prediction，那么可以直接将相应的局部特征提取出来就可以了，但是如果要做 graph classification，那么接着还需要对于整个图的全局信息进行聚合。之前做法的方式是直接聚合，比如把所有节点的特征加合起来，而忽略了各个节点之间可能的复杂层次关系；也有方法提出采取分开的两步，即先做 message passing，再做 graph clustering。如果把 GNN 和 CNN 网络对比，会发现这之前的 GNN 只是相当于一层的 CNN，只能在原本的图结构上做一次信息抽取，不能再在更粗的粒度上做信息抽取。

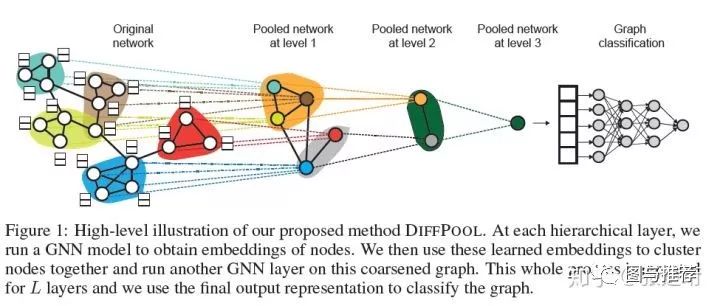
这里提出的方法就是要构建一个多层次的 GNN 网络，在每一层中，不仅需要完成信息的抽取（在图上进行多次信息传递），而且需要把当前的图聚合为一个更粗粒度的图，供下一层使用。类比 CNN，在 CNN 中，图信息的聚合是自然完成的，因为在图片里面距离近的像素具有天然的临近关系，可以直接 MaxPooling、AvgPooling 等办法完成聚合；而在一般的图里面这件事情就比较困难了。文章这里提出如下图所示的框架，在做完之前的 GNN 操作之后，再利用这里提出的 DiffPool 方法自动聚合节点，然后把新聚合出来的节点当做新的图再利用之前的 GNN 算法来抽取信息，如此多层信息抽取，最后得到一个单一节点的特征。最后利用这个单一节点的特征来做 graph classification。

2. 之前的 GNN 模块

一个之前的 GNN 算法可以被表示为，其中是图的邻接矩阵，为所有节点上的特征组成的矩阵，每个节点的特征都是一个 d 维的向量，是抽取出来的每个节点上的特征。一般一个 GNN 的神经网络由若干次信息传递组成，可以表示为

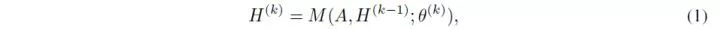
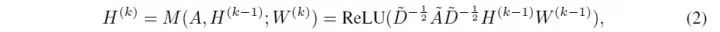
其中 k 表示第 k 次信息传递，为相应神经网络的参数。在第一次信息传递中，H 就是输入的原始节点特征矩阵 X；在最后一次信息传递中，相应的 H 就作为 Z 输出。比较著名的 GCN 算法的信息传递公式可以写为

3. 算法

文章提出做可微分、端到端的多层的 GNN 框架（differentiable and end-to-end）。对于第 l 层来说，数学上可以写为

其中每次通过一次 DiffPool，相应的节点个数都会减少；在通过最后一次 DiffPool 之后，规定只留下一个节点；假设该节点包含一个 d 维的向量，最后就从这个 d 维向量出发得到最后的 graph classification。

下面我们会讲具体这个 DiffPool 过程包含什么内容。

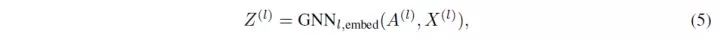
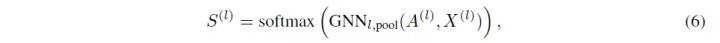
首先，不仅使用一个 GNN 来抽取信息得到 Z，而且还使用另外一个 GNN 来得到权重矩阵（assignment matrix），它表示了每一个上一层中的节点以多大的权重被分配到下一层的哪些节点中。

接下来，通过如下形式来产生新一层节点的邻接矩阵和每个节点的特征，可以看出，其实就是根据学习到的权重矩阵来进行加权聚合。

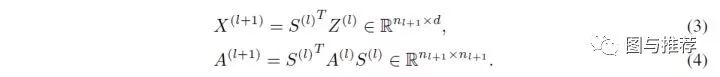
4. 正则化

到此为止，一切看起来都挺合理并且也很自然，但是一般这样简单的方案实际中肯定很难有效，因为这个方案自由度还挺大的，学起来并不容易，光看公式 (3) 和 (4) 就知道，矩阵乘法里面很多部分都需要学习。因此，要使得这个方案能够有效，就需要加上一些正则化项，避免它学成我们不想要的结果。

文章加了如下正则项：

Auxiliary Link Prediction：最小化，这里表示 Frobenius norm，中间的逗号没太明白，我理解应该就是相减。比划一下，我感觉其含义就是要求生成的下一层邻接矩阵尽量为一个 identity matrix，即图像一条链；我没跑过实验，不知道不要这一项会怎样，我感觉如果没有这个的话，可能会导致一些 trivial 的情形，比如所有的节点都映射到下一层的同一个节点上。
Entropy：最小化，表示对于 S 矩阵中每一行熵的平均。我感觉如果不加这一项，可能出现另外的 trivial 的情形，比如在下一层形成一个全连接的图，然后每一个节点都等权映射到新节点上。
L2 Regularization：在 GNN 之后，对产生的 node embedding 做 L2 regularization，文章说这样会更稳定。

5. 实验

实验当然是对比之前的 GNN 网络对比性能，同时也展示一下节点聚合的效果。让我比较感兴趣的是，文章中写道他们观察到如下现象：有两类节点会被聚合到一起，一类是连接距离上比较近的节点，一类是特征上比较类似的节点。在 RL 中，如果把状态当做节点，前一种聚类方式就好像把邻近节点（比如和）聚合到一起；后一种聚类方式就好像姜楠课件里面讲的 bisimulation。那么问题来了，究竟哪一种聚合方式（或者混合）更好？理论上怎么说？

参考文献

[1] Gilmer, Justin, et al. "Neural message passing for quantum chemistry." Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR. org, 2017.

登录查看更多