如何从海量数据中找到相似数据--那些用于查找相似数据的哈希算法（2）

2017 年 10 月 30 日 中国科学院网络数据重点实验室 王永庆

目录

布隆过滤器（BloomFilter）
Simhash
Minhashing
局部敏感哈希（Local Sensitive Hashing）

前言：接上文，本篇所讲的两种哈希算法：minhashing和局部敏感哈希（LSH）是一类哈希的思路，可以用来在海量数据中查找相似的短语、句子、文档。

4 Minhashing

Minhashing主要适用于匹配词、句等相对较短的内容的匹配。Minhashing的基本思想近似于对数据做特征映射：将原数据按照一定的规则抽取出固定大小的特征，由抽取的特征判断数据间的相似程度。一般认为，特征化的数据比原数据更易执行匹配操作。

接下来，我们来看下minhashing是如何完成从原始数据到数据特征的转换，并保持数据间的相似信息。

Step 1. 对原数据进行切分；

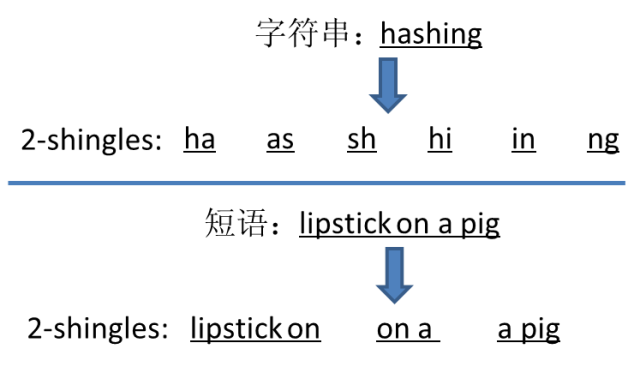
对数据的切分一般会依据不同的任务而做不同的设置。例如，在对单词做相似度匹配时，可以采用k-shingles方法：对一个长度为n的字符串，设置一个长度为k(k<n)的窗口，取字符串中所有符合该窗口大小的子串。如果对短语或句子做相似度匹配，窗口可以以单词为单位。

图3 k-shingles示例(k=2)

Step 2. 用切分所得的数据集合对原数据进行标注；

用一个简单的例子展示该步骤。我们取1-shingle情况，对4个字符串（“ad”，“c”，“bed”，“adc”）进行切分（step 1操作），得到集合S1={a,d}, S2={c}, S3={b,d,e}, S4={a,c,d}。则标注后的数据为

图 4 数据标注后的结果

Step 3. 数据特征化。

在这一步骤中会采用到hash方法，同时大家也能理解为何取名为“minhash”。此处的数据特征化共需经历两个步骤。

3.1 hash计算

利用hash方法对标注数据进行编码，进而起到数据压缩的作用。再者，编码后的数据更容易在编码后的空间中进行比较（hash方法的基本思想）。

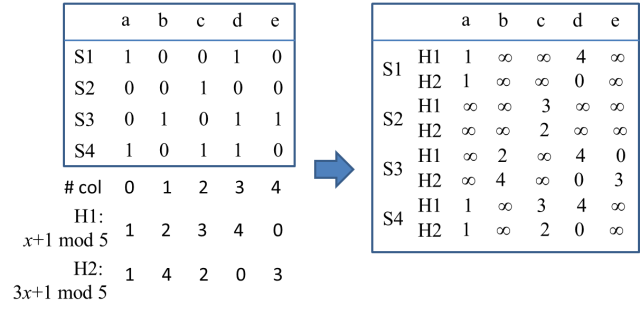
举个例子，我们通过两个hash函数（H1和H2），对step 2中的示例数据进行hash编码，其规则为：按列对数据进行编码，如果对应的字符串中出现该子串（对应位置标注为1），则取对应列的hash编码，否则置为无穷大∞（见图5示例）。

图 5 一种hash计算方法

3.2 Minhashing

对上一步计算得到的hash值进行压缩，生成对应字符串的minhash值。具体的方式为：对由每一个hash函数产生的hash值，取最小值。例如，字符串“ad”（S1集合表示）由H1计算所产生的minhash值为1（1<4<∞）。依次类推，可以得到所有字符串的minhash值。根据上一示例的结果，我们可以得到表1中结果。

表 1 对应图5所得到的minhash值

	S1	S2	S3	S4
H1	1	3	0	1
H2	0	2	0	0

我们可以发现，S1和S4集合的minhash值完全一致。通过minhash值判断，对应字符串相似（对应字符串为“ad”，“adc”）。

归纳上述步骤，我们可以得到minhashing的处理流程：

初始化：m个hash函数

输入：数据集合D={d₁, d₂,…,d_n}

For i=1 to n

（k-shingles）将d_i按照窗口大小k进行切分；
（数据标注）将切分所得的数据单元标注一个全局的类别码（相当于给各数据单元一个列号）；
（计算minhash值）用m个hash函数计算对应的hash值，并取minhash记录。

End for

输出：所有文档D的minhash值

使用minhashing的注意事项：

切分、标注后数据只保留了大小为k的序关系，子串间无顺序关系，因此Minhashing是一种对局部序关系敏感的匹配方法；
Minhashing的数据特征化可以采用其他方式，使得数据可以在不同度量空间中进行匹配；
采用k-shingles方法时，需要结合具体的应用场景，过小的k值会让匹配范围增大；而过大的k值则会增加存储代价（可能的子串数量增加），同时降低了匹配范围；
Hash函数的数量决定了minhashing方法的匹配效率，随着hash函数数量增加，匹配精度逐渐提升，并同时增加数据匹配的计算开销。

5 局部敏感哈希（Local Sensitive Hashing）

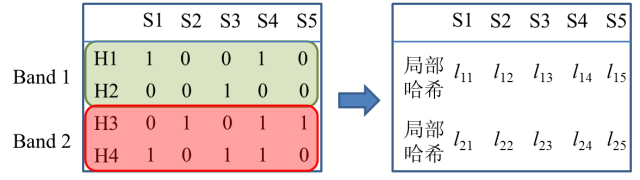
设想在数据集规模较大的情况下，采用minhashing方法的一种场景：需要处理的数据本身具有一定的复杂性（例如：句子、短语等），我们需要通过较多的hash函数（例如k>100）来提取足够的minhash值进行数据匹配。Minhashing的匹配效率会随选择的hash函数增加而降低，从而限制了方法的适用场景。为了解决这一问题，在minhashing的基础上，进一步地提出了局部敏感哈希方法。局部敏感哈希适用于短语、句子、篇章级的大规模匹配任务，其基本思想为：在minhashing基础上，将minhashing值划分为若干个不同的区域（局部概念），比较区域内的数据一致性（仍然利用hash编码）。

图 6 在minhashing基础上的局部敏感哈希示例

局部敏感哈希的处理过程：

初始化：m个hash函数，信道（band）大小r，信道数量b

输入：数据集合D={d₁, d₂,…,d_n}

For i=1 to n

采用minhashing方法获得m个minhash值；
将m个minhash值按照顺序划分为b个信道，每个信道中有序平均分布r个minhash值，并将每个信道进行hash编码；
记录每个信道所得的hash值。

End for

输出：所有文档D的在各个信道上的hash值

使用局部敏感哈希的注意事项：

1. 在局部敏感哈希的计算过程中，所选择的hash函数，一般要选择同一族的；

所谓同一族的哈希函数是指族内的哈希函数具有相同的区别能力。例如，前例中的两个哈希函数x+1 mod 5和3x+1 mod 5就属于同一族。选用同一族的哈希函数更利于我们在数学上分析获得数据匹配的准确程度，便于确定信道大小和信道数量。具体详见《Mining of Massive Datasets》的第三章节介绍。

2. 在局部敏感哈希中，各个信道内，执行匹配的“与”操作，只有匹配数据完全一致时，才能产生一致的局部哈希值。而在各个信道间执行匹配的“或”操作，任意信道存在一处一致的哈希值，即认为匹配成功；

3. 局部敏感哈希中的参数r和b联合控制最终的匹配精度。

参考文献

J. Leskovec, A. Raj., J.D. Ullman. Mining of Massive Datasets, 2011.
http://www.lanceyan.com/tag/simhash
http://www.cnblogs.com/haippy/archive/2012/07/13/2590351.html

小记

在实际的工程应用中，确实存在很多在研究环境下不曾遇到的挑战。重新去检视这些经典，而不再是沉溺于过去的思维方式，倒是又有很多新的收获。我们在目前的工作，已经将局部敏感哈希应用于相关场景的问题处理上，LSH的相关代码可见：https://github.com/Allen517/alignment/blob/master/portrait/gadget/LSHCache.py。

欢迎关注作者微信公众号